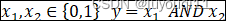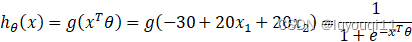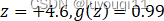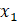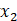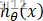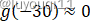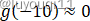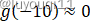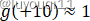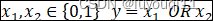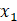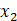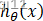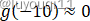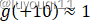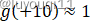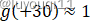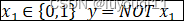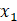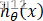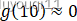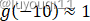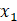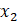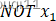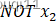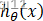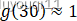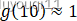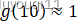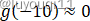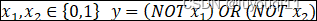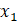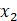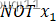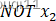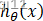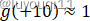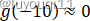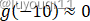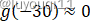机器学习(14) 运用神经元解决同或(XNOR)、异或(XNOR)分类问题

1 与、或、非、与非、或非、异或、同或的概念

与(AND)

与门（英语：AND gate）又称“与电路”、逻辑“积”、逻辑“与”电路。是执行“与”运算的基本逻辑门电路。有多个输入端，一个输出端。当所有的输入同时为高电平（逻辑1）时，输出才为高电平，否则输出为低电平（逻辑0）。

或(OR)

或门（OR gate），又称或电路、逻辑和电路。如果几个条件中，只要有一个条件得到满足，某事件就会发生，这种关系叫做“或”逻辑关系。具有“或”逻辑关系的电路叫做或门。或门有多个输入端，一个输出端，只要输入中有一个为高电平时（逻辑“1”），输出就为高电平（逻辑“1”）；只有当所有的输入全为低电平（逻辑“0”）时，输出才为低电平（逻辑“0”）。

非(NOT)

非门（英文：NOT gate）又称非电路、反相器、倒相器、逻辑否定电路，简称非门，是逻辑电路的基本单元。非门有一个输入和一个输出端。当其输入端为高电平（逻辑1）时输出端为低电平（逻辑0），当其输入端为低电平时输出端为高电平。也就是说，输入端和输出端的电平状态总是反相的。非门的逻辑功能相当于逻辑代数中的非,电路功能相当于反相,这种运算亦称非运算。

异或（XOR）

异或门 （英语：Exclusive-OR gate，简称XOR gate，又称EOR gate、ExOR gate）是数字逻辑中实现逻辑异或的逻辑门。有多个输入端、一个输出端，多输入异或门可由两输入异或门构成。若两个输入的电平相异，则输出为高电平1；若两个输入的电平相同，则输出为低电平0。即如果两个输入不同，则异或门输出高电平1。

同或（XNOR）

同或门（英语：XNOR gate或equivalence gate）也称为异或非门，在异或门的输出端再加上一个非门就构成了异或非门，是数字逻辑电路的基本单元，有2个输入端、1个输出端。当2个输入端中有且只有一个是低电平（逻辑0）时，输出为低电平。亦即当输入电平相同时，输出为高电平（逻辑1）。

2 神经元实现与(AND)

现在来看看神经网络是如何实现与门的。

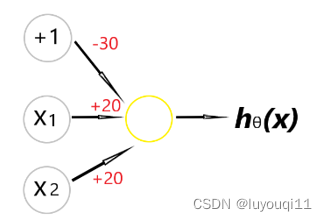
我们增加一个单元x0=1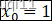，给三个单元分别赋予权重-30、+20、+20。则有

则有：

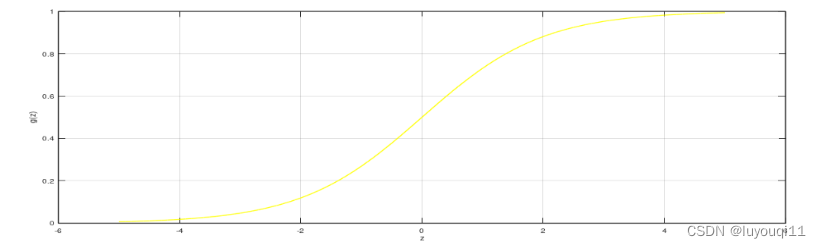
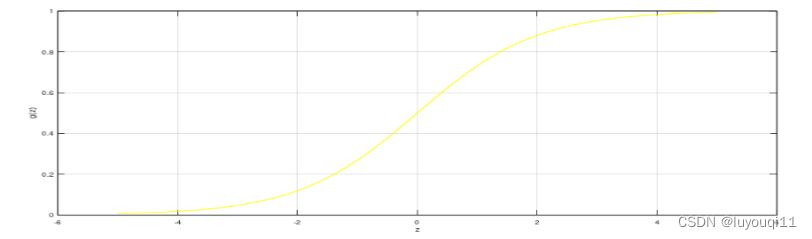
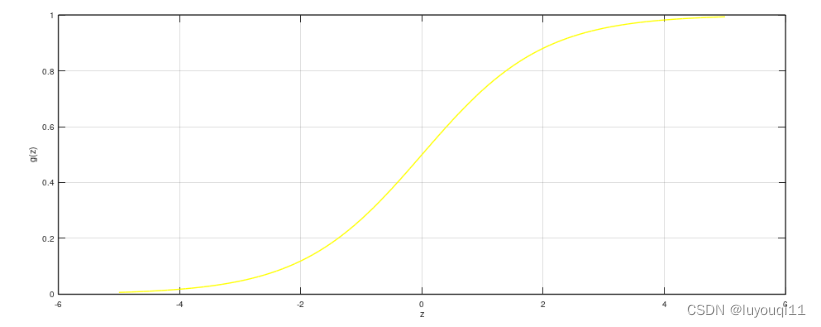
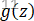
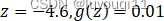
我们已知的图像如下：当，当

根据图像，就有：

这样神经元就实现了与门(AND)。

3 神经元实现或(OR)

我们增加一个单元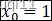，给三个单元分别赋予权重-10、+20、+20。则有

根据图像，就有：  

这样神经元就实现了或门(OR)。

4 神经元实现非(NOT)

我们增加一个单元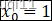，给三个单元分别赋予权重10、-20、0。则有

这样神经元就实现了非门(NOT)。

5 神经元实现异或(XOR)

等价于如果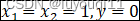，否则y=1

我们增加一个单元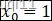，给三个单元分别赋予权重30、-20、-20。则有

这样神经元就实现了NOT x1 AND (NOT x2)。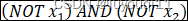

6 神经元实现同或(XNOR)

等价于如果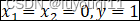，否则y=0

我们增加一个单元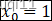，给三个单元分别赋予权重10、-20、-20。则有

这样神经元就实现了。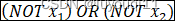

7 对神经网络的理解

因此，对神经网络更直观的理解就是，它通过大量的隐藏层网络将输入向量进行一步又一步的抽象（加权求和+非线性变换），生成能够更加容易解释模型的复杂新特征，最后将这些强大的新特征传入输出层获得预测结果。就像单层神经元（无隐藏层）无法表示逻辑同或运算，但是若加上一个隐藏层结构就可以轻松表示出逻辑同或运算！

今天的文章机器学习(14) 运用神经元解决同或(XNOR)、异或(XNOR)分类问题分享到此就结束了，感谢您的阅读。