美赛2020题目b_组合优化的遗传算法

A题是自由度比较大的场景限定下的模型构建，相对比较容易，核心是找到现有的成熟的数学模型，然后找到合适的数据进行证明得到结论，估计大部分是目标优化问题。（不限制专业）

B题属于较为经典的物理建模（对海洋专业的学生具有优势）

C题今年非常难，不同往年的数据分析，不过核心还是特征提取和主成分分析(本质是在数据中找到或者构建影响比赛的有效向量)，并且需要在其他数据上证明推广(这点就比较恶心了) （不限制专业）

D 本质上是资源分配和调度问题，其中保持最佳水位需要一个控制算法(估计要融合PID或者模糊PID)，其中也会涉及到目标优化模型（毕竟多方需要争抢湖泊的水位），需要做灵敏度分析。难度不小！

E 核心是做相关性分析，并涉及到评价模型，就是数据会比较难找！

F 本次建模最简单的一道题，给定一个范围甚至目标都需要自己定，并且动物保护相关数据比较好找，最后结合语文建模就能搞定！

难度排名（由易到难）：F < A < E < D < B < C

选题建议：建议优先F、A题，C题难度大，竞争也大，获奖率低！！！

经过不懈的努力，2024美赛A题完整中文版和英文版论文和代码已完成，代码为A题全部4问的代码，论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解（问题1七鳃鳗种群竞争模型的建立和求解、问题2种群优势劣势评估模型的建立、七鳃鳗种群复杂系统动力学模型建立和求解、七鳃鳗与寄生物种群之间的相互作用模型建立和求解）、模型灵敏性分析、模型的评价等等，完整版本见文末

中文版预览如下：

英文版预览如下：

首先是论文摘要，部分摘要如下：
一、摘要
七鳃鳗是一种兼具食物链底层和中层角色的鱼类。其性别比例会因环境资源条件而发生变化。为评估这一适应策略对生态系统的影响,建立了考虑七鳃鳗数量动态、性别结构演化的动力学模型。模型连接七鳃鳗性别比例与资源可用性,模拟不同参数下的动态演化过程。研究了四个方面的问题:七鳃鳗性别比例变化对环境的影响,这种适应性的优劣势评估,对生态系统稳定性的影响,以及对寄生生物的影响。
问题一通过建立考虑七鳃鳗数量动态、性别比例与环境资源相互作用的定量关系模型,预测并分析了不同情景下七鳃鳗性别比例失调可能在更大生态系统中引起的连锁反应。结果表明,作为重要的食物链连接环节,七鳃鳗性别结构的高度可塑性虽提高了其自身的适应能力,但也增加了整个生态系统的不确定性,可能导致多种生物种群数量和分布的剧烈波动。
问题二通过评估性别比例变化对七鳃鳗自身繁殖和外部捕食压力的影响,深入考察了这一适应策略的优劣势所在。建模结果显示,尽管这种可塑性增强了面对资源匮乏的获能力,但种群内部的性别比例失衡又增加了近亲交配的可能,降低了遗传多样性。此外,七鳃鳗性别比例的大幅波动也对依赖其存活的寄生物种和捕食性鱼类造成不同程度的生存压力。
问题三通过引入竞争种群,建立了七鳃鳗与其他物种相互作用的动力学模型,并讨论了不同情景下的演化趋势。连接了食物供应量与七鳃鳗性别比例的定量关系,结果发现依赖单一食源的七鳃鳗种群更易在食物供应变化时遭受灭绝的威胁。与多种食源的种群相比,这类种群对环境扰动的抵抗能力较弱,其自身波动也更剧烈地影响着其他依赖种群的存活。
问题四（见完整版）
本文通过建模的方法全面评估了七鳃鳗这一适应策略的利弊。模型考虑了多种生态学因素的相互作用,参数设置具有一定的生物学意义。不足之处在于对某些过程简化程度较高,没有建模随机扰动的影响。后续工作将在模型预测的基础上,收集实验数据进行验证,以提供科学的生态系统管理建议。
关键词：七鳃鳗,动力学模型,性别比例,竞争种群 ,灵敏度分析
目录
一、摘要… 1
二、问题重述… 3
三、问题分析… 3
3.1 问题一分析… 3
3.2 问题二分析… 4
3.3 问题三分析… 4
3.4 问题四分析… 5
四、模型假设… 5
五、符号说明… 6
六、模型的建立和求解… 7
6.1 问题一模型的建立… 7
6.1.1 七鳃鳗种群竞争模型的建立… 7
6.1.2 仿真参数设置… 9
6.2 问题二模型的建立… 10
6.2.1 种群优势劣势评估模型的建立… 10
6.2.2 仿真参数设置… 12
6.2.3 仿真结果可视化… 13
6.3 问题三模型的建立… 13
6.3.1 七鳃鳗种群复杂系统动力学模型建立… 13
6.3.2 仿真参数设置… 15
6.3.3 性别比例与食物供应的关系模型… 18
6.4 问题四模型的建立… 21
6.4.1 七鳃鳗与寄生物种群之间的相互作用模型建立… 21
6.4.2 仿真参数设置… 23
6.4.3 求解结果可视化… 24
七、模型的灵敏度分析… 24
八、模型的评价… 25
8.1 模型的优点… 25
8.2 模型的不足… 25
8.3 模型的展望… 25
一、问题重述
2024美赛A题问题重述如下：虽然一些动物物种存在于通常的雄性或雌性之外，但大多数物种基本上要么是雄性，要么是雌性。尽管许多物种在出生时表现出1:1的性别比例，但其他物种偏离了均匀的性别比例。这被称为适应性性别比例变化。例如，孵化美洲短吻鳄蛋的巢穴温度会影响出生时的性别比例。
七鳃鳗的角色很复杂。在一些湖泊栖息地，它们被视为对生态系统有重大影响的寄生虫，而七鳃鳗也是世界上一些地区的食物来源，如斯堪的纳维亚半岛、波罗的海国家和北美太平洋西北部的一些土著人民。
七鳃鳗的性别比例会因外部环境而异。七鳃鳗是雄性还是雌性取决于它们在幼体阶段的生长速度。这些幼虫的生长率受食物供应的影响。在食物供应不足的环境中，增长率会更低，男性比例可达到人口的约78%。在食物更容易获得的环境中，观察到男性的比例约占人口的56%。
我们关注性别比例及其对当地条件的依赖问题，特别是对七鳃鳗而言。七鳃鳗生活在湖泊或海洋栖息地，并迁移到河流上游产卵。任务是检查一个物种根据资源可用性改变其性别比例的能力的优缺点。你的团队应该开发并检查一个模型，以提供对生态系统中产生的相互作用的见解。
要检查的问题包括以下内容:
· 问题一：当七鳃鳗的数量可以改变其性别比例时，对更大的生态系统有什么影响？
· 问题二：七鳃鳗种群的优势和劣势是什么？
· 问题三：鉴于七鳃鳗性别比例的变化，对生态系统的稳定性有什么影响？
· 问题四：七鳃鳗种群中性别比例可变的生态系统能否为生态系统中的其他物种（如寄生虫）提供优势？
二、问题分析
2.1 问题一分析
2024美国大学生数学建模竞赛A题问题1的分析：当七鳃鳗的数量可以改变其性别比例时,对更大的生态系统会产生影响。这些影响主要包括生态平衡的扰动、种群动态的改变、生态功能的变化以及生态系统稳定性的下降。
七鳃鳗作为生态系统中的重要成员,其数量和性别比例的变化会导致资源利用模式和竞争关系的改变。这可能扰乱原有的生态平衡,需要一定时间才能达到新的平衡状态。
此外,七鳃鳗数量和性别比例的变化也会改变整个种群的动态过程。如果某一性别的七鳃鳗数量显著减少,会降低整个种群的繁殖能力。
七鳃鳗在生态系统中扮演着多重角色,作为食物链中的捕食者、被捕食者及其他物种的食物来源。性别比例变化后,其在食物网中的作用也会发生改变。
如果七鳃鳗的数量或某一性别比例失控,很可能会加剧资源竞争,最终威胁到生态系统的整体稳定性。
2.2 问题二分析
2024美国大学生数学建模竞赛A题问题2的分析：当七鳃鳗能够根据资源条件改变其性别比例时,这种适应性会带来一定的优势,也存在一定的劣势。
优势:
这种适应性可以帮助七鳃鳗种群更好地利用环境资源,提高其数量,获取更高的适应度。
性别比例的调整有利于维持种群的繁殖能力。当资源减少时,可以适当增加雌性个体的比例。
这种适应策略使七鳃鳗种群更加灵活,能更好应对环境压力和资源缺乏的威胁。
劣势:
性别比例失衡时很容易导致近亲交配的发生,降低种群的遗传多样性。
七鳃鳗性别比例的大幅波动可能会影响捕食七鳃鳗的其他物种的数量。
性别比例快速变化可能会打破种群原有的动态平衡,需要耗费时间和资源重新建立平衡。
2.3 问题三分析
七鳃鳗能够根据食物供应调整其性别比例会对生态系统的稳定性产生一定的影响。主要体现在以下几个方面:

性别比例改变会影响七鳃鳗自身的种群动态,进而波及依赖七鳃鳗的其他物种。
不同性别个体在捕食和生长方面可能存在差异,这会改变它们对下游食物来源的利用模式。
性别比例失衡时很容易导致近亲交配,这会降低遗传多样性,不利于长期种群增长。
七鳃鳗性别比例的快速波动可能会打破种群和更大生态系统原有的平衡,需要时间重建。
性别比例与食物供应之间的动态波动本身就增加了生态系统的不确定性。
2.4 问题四分析
七鳃鳗性别比例的变化对寄生生物种群会产生一定的影响:
寄生物依赖七鳃鳗生存和繁殖,七鳃鳗数量的变化会直接影响寄生物数量。
不同性别的七鳃鳗可能对寄生物的抵抗力不同,这会改变寄生物感染和扩散的模式。
性别比例失衡时很容易导致近亲交配,这会降低遗传多样性,长期不利于抵抗寄生物。（见完整版）
三、模型假设
本文的模型假设主要有以下几点：
七鳃鳗的数量和性别比例会受到环境资源条件的影响。
七鳃鳗种群中雄性和雌性个体的生长与死亡规律可以用相对于资源条件和自身数量的一阶线性微分方程描述。
七鳃鳗的繁殖成功率与雌性七鳃鳗的数量和性别比例相关。
捕食七鳃鳗的其他物种数量与七鳃鳗总体数量相关。
七鳃鳗与其他生物种群之间存在竞争关系,可以用物种间的竞争系数描述。（见完整版）
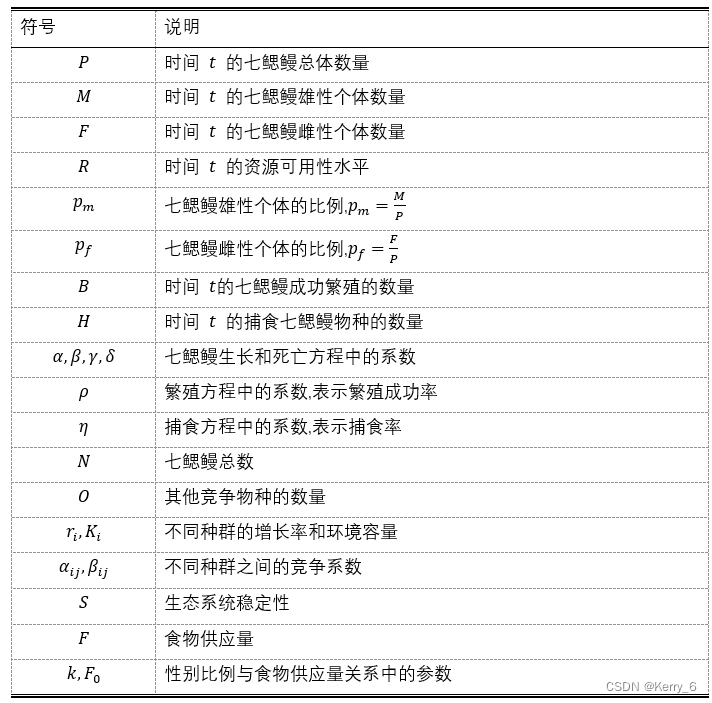
四、符号说明
以下是本文使用的符号及其说明：

六、模型的建立和求解
中间模型略，见完整版
6.3 问题三模型的建立
2024美国大学生数学建模竞赛A题问题三要求研究七鳃鳗种群根据资源可用性调整性别比例对更大生态系统的影响，特别是对其他生态系统成员的影响。我们将考虑与其他物种的相互作用，包括竞争和捕食。我们将引入另一种生态类型的物种，并研究其与七鳃鳗种群的相互作用。
6.3.1 七鳃鳗种群复杂系统动力学模型建立
为了建立一个更复杂的系统动力学模型来分析七鳃鳗种群的动态行为，我们将结合多物种的竞争模型、logistic增长模型和前文建立的模型。我们将考虑七鳃鳗种群与其他物种之间的竞争、食物链关系以及性别比例的变化对整个生态系统的影响。

然后，我们建立以下方程来描述这些变量之间的关系：

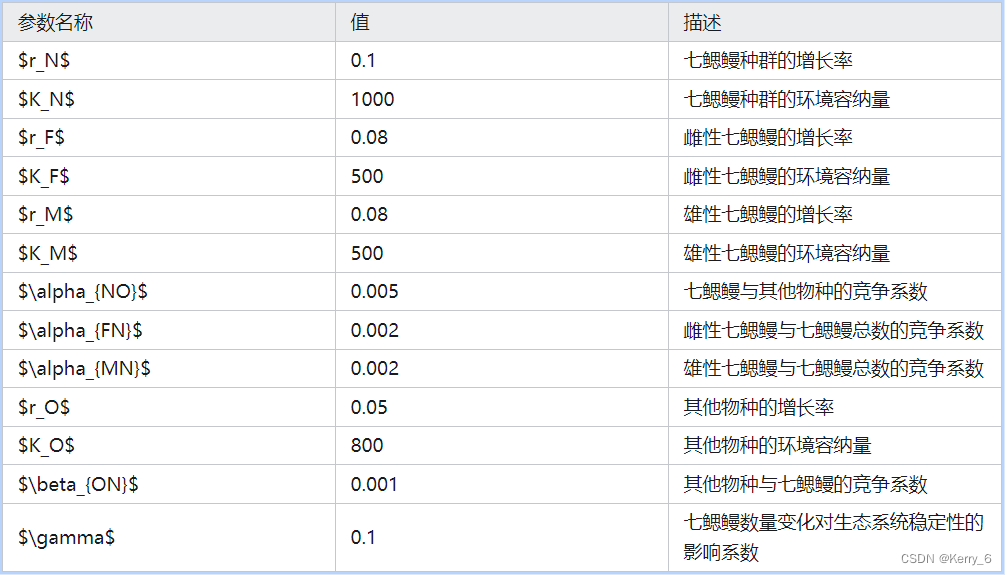
仿真参数设置
为了使用 MATLAB 对七鳃鳗种群的复杂系统动力学模型进行可视化分析，我们编写一个 MATLAB 脚本来模拟系统动力学模型，并观察七鳃鳗数量、性别比例以及其他物种数量的变化。我们首先需要设定合理的参数，然后使用 MATLAB 的 ODE45 函数来解决微分方程，并将结果可视化。为了对七鳃鳗种群复杂系统动力学模型进行仿真，我们使用以下的参数设置

%% 先建立较简单的模型：七鳃鳗数量、性别比例以及其他物种数量的变化模型
% 参数设置
r_N = 0.1;  % 七鳃鳗种群的增长率
K_N = 1000; % 七鳃鳗种群的环境容纳量
r_F = 0.08; % 雌性七鳃鳗的增长率
K_F = 500;  % 雌性七鳃鳗的环境容纳量
r_M = 0.08; % 雄性七鳃鳗的增长率
K_M = 500;  % 雄性七鳃鳗的环境容纳量
alpha_NO = 0.005; % 七鳃鳗与其他物种的竞争系数
alpha_FN = 0.002; % 雌性七鳃鳗与七鳃鳗总数的竞争系数
alpha_MN = 0.002; % 雄性七鳃鳗与七鳃鳗总数的竞争系数

% 定义微分方程
dydt = @(t, y) [
    r_N * y(1) * (1 - y(1)/K_N) - alpha_NO * (y(1) - y(4)); % 七鳃鳗种群动态方程
    r_F * y(2) * (1 - (y(2) + y(3))/K_F) + alpha_FN * (y(1) - y(2)); % 雌性七鳃鳗动态方程
    （见完整版本）
    r_O * y(4) * (1 - y(4)/K_O) - beta_ON * (y(4) - y(1)) % 其他物种动态方程
];

% 初始条件
initial_condition = [100, 50, 60, 200];

% 解决微分方程
（见完整版本）

% 可视化结果
figure;
plot(t, y(:,1), 'b', t, y(:,2), 'r', t, y(:,3), 'g', t, y(:,4), 'k');
xlabel('时间');
ylabel('数量');
legend('七鳃鳗总数', '雌性七鳃鳗数量', '雄性七鳃鳗数量', '其他物种数量');
title('七鳃鳗种群动态行为');
exportgraphics(gcf, 'img/问题3七鳃鳗种群动态行为.png', 'Resolution', 300);

% 绘制相图
figure;
plot(y(:,1), y(:,2), 'b');
xlabel('七鳃鳗总数');
ylabel('雌性七鳃鳗数量');
title('相图');
exportgraphics(gcf, 'img/问题3雌性七鳃鳗数量与七鳃鳗总数的相图.png', 'Resolution', 300);

% 绘制相平面
figure;
plot3(y(:,1), y(:,2), y(:,3), 'r');
xlabel('七鳃鳗总数');
ylabel('雌性七鳃鳗数量');
zlabel('雄性七鳃鳗数量');
title('相平面');
exportgraphics(gcf, 'img/问题3雄性七鳃鳗数量、雌性七鳃鳗数量与七鳃鳗总数的相平面.png', 'Resolution', 300);

% 绘制七鳃鳗数量随时间变化的时间序列
figure;
plot(t, y(:,1), 'b');
xlabel('时间');
ylabel('七鳃鳗总数');
title('七鳃鳗数量随时间变化的时间序列');
exportgraphics(gcf, 'img/问题3七鳃鳗数量随时间变化的时间序列.png', 'Resolution', 300);

% 绘制七鳃鳗性别比例与其他物种数量的关系

figure;
plot(y(:,3)./y(:,2), y(:,4), 'b');
xlabel('性别比例（雄性/雌性）');
ylabel('其他物种数量');
title('七鳃鳗数量随性别比例变化的时间序列');
exportgraphics(gcf, 'img/问题3七鳃鳗数量随性别比例变化的时间序列.png', 'Resolution', 300);

我们先定义了系统的参数，然后定义了微分方程，并使用 ode45 函数解决微分方程。最后，我们将结果可视化，以观察七鳃鳗种群的动态行为，并进一步分析七鳃鳗数量和性别比例变化对整个生态系统的影响。
仿真结果如下：

七鳃鳗种群动态行为（略，见完整版）
在 MATLAB 中，我们可以通过绘制相图和相平面来观察系统的平衡点和稳定性，通过分析时间序列来判断系统是否呈现周期性或混沌行为。

雌性七鳃鳗数量与七鳃鳗总数的相图（略）
雄性七鳃鳗数量、雌性七鳃鳗数量与七鳃鳗总数的相平面（略）
七鳃鳗数量随性别比例变化的时间序列
我们使用了相图来可视化七鳃鳗总数与雌性七鳃鳗数量之间的关系，使用相平面来可视化七鳃鳗总数、雌性七鳃鳗数量和雄性七鳃鳗数量之间的关系，以及使用时间序列来观察七鳃鳗数量随时间的变化。
最后，我们根据建立的生态系统的稳定性方程计算得到生态系统的稳定性随性别比例变化曲线如图
问题3生态系统的稳定性随性别比例变化
性别比例与食物供应的关系模型
七鳃鳗的性别比例会因外部环境而异。七鳃鳗是雄性还是雌性取决于它们在幼体阶段的生长速度。
为了将性别比例与食物供应的关系融合进上面的系统动力学方程，我们可以假设性别比例的变化受到食物供应的影响，进而影响到雌性和雄性七鳃鳗的出生率。我们可以使用一个简单的函数来描述性别比例与食物供应之间的关系，然后将其应用于出生率的计算中。

然后，我们可以修改之前的系统动力学方程，将性别比例与食物供应的关系融入其中。假设雌性七鳃鳗的出生率与食物供应成正比，而雄性七鳃鳗的出生率与食物供应和性别比例相关。
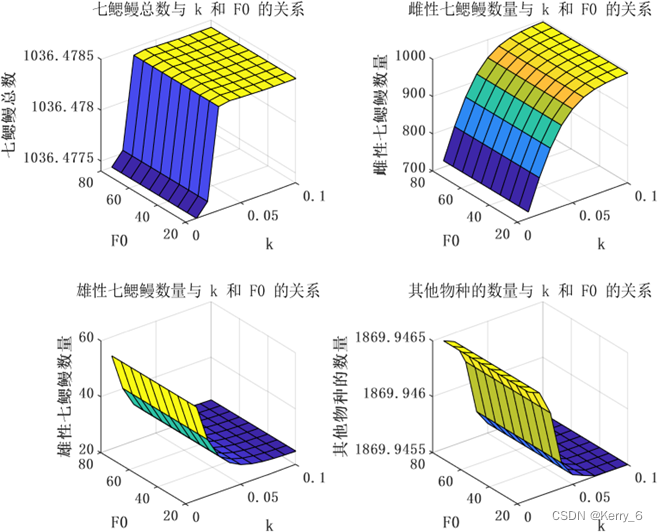
遍历参数 k 和 F0，并绘制稳态时的七鳃鳗总数、雌性七鳃鳗数量、雄性七鳃鳗数量、其他物种的数量与 k 和 F0 的关系，以及稳态时的其他物种的数量与稳态时的性别比例的关系。

七鳃鳗总数、雌性七鳃鳗数量、雄性七鳃鳗数量和其他物种的数量与 k 和 F0 的关系
七、模型的灵敏度分析
美赛中模型的灵敏度分析很重要，为了分析建立的模型中不同参数对系统动态演化过程的影响程度,即参数对系统输出灵敏度的大小,进行下面的灵敏度分析:
固定其他参数,改变目标参数,比如生长率参数 $\alpha$ ,在一定范围内进行多次求解。
分析目标输出变量,如稳态时七鳃鳗种群数量 $P$ 对参数 $\alpha$ 的灵敏度:

重复上述过程,可以得到输出 $P$ 对各个参数的灵敏度大小。（见完整版）

下面是A题思路，文末有进阶思路

要建立一个数学模型来解决问题1，我们可以考虑以下几个关键因素：

七鳃鳗的种群数量（总数）
雌性七鳃鳗的数量
雄性七鳃鳗的数量
外部环境因素（例如食物供应）对七鳃鳗性别比例的影响

我们可以使用一个简单的差分方程模型来描述七鳃鳗种群数量和性别比例的变化。假设我们用 $N$ 表示七鳃鳗的总数， $F$ 表示雌性七鳃鳗的数量， $M$ 表示雄性七鳃鳗的数量。然后，我们可以建立以下差分方程：

$\frac{ {dN}}{ {dt}} = \text{出生率} – \text{死亡率}$

$\frac{ {dF}}{ {dt}} = \text{雌性出生率} – \text{雌性死亡率}$

$\frac{ {dM}}{ {dt}} = \text{雄性出生率} – \text{雄性死亡率}$

出生率和死亡率可以取决于许多因素，包括资源可用性、捕食压力等等。为了模拟性别比例的变化，我们可以假设七鳃鳗性别比例的变化受到外部环境因素的影响，比如食物供应。这可能导致雄性和雌性七鳃鳗的出生率和死亡率发生变化。

为了描述七鳃鳗性别比例的变化受到外部环境因素（如食物供应）的影响，我们可以修改之前提到的差分方程模型，使其考虑到这些影响。我们可以假设食物供应对七鳃鳗的生长速率有直接影响，并进而影响到雌性和雄性七鳃鳗的出生率。我们用 $R$ 表示食物供应的水平，然后可以将出生率的表达式修改为：

$\text{雌性出生率} = \alpha \cdot R$

$\text{雄性出生率} = \beta \cdot R$

其中， $\alpha$ 和 $\beta$ 是与食物供应相关的参数，表示雌性和雄性七鳃鳗出生率与食物供应水平的比例关系。

在这个模型中，我们假设雌性和雄性七鳃鳗的死亡率与食物供应无关，综合起来，完整的模型可以表示为以下差分方程组：

$\frac{ {dN}}{ {dt}} = \text{出生率} – \text{死亡率}$

$\frac{ {dF}}{ {dt}} = \alpha \cdot R – \text{雌性死亡率}$

$\frac{ {dM}}{ {dt}} = \beta \cdot R – \text{雄性死亡率}$

其中， $\alpha$ 和 $\beta$ 是食物供应影响参数， $R$ 是食物供应水平， $N$ 表示七鳃鳗的总数， $F$ 表示雌性七鳃鳗的数量， $M$ 表示雄性七鳃鳗的数量。

为了建立七鳃鳗数量与更大生态系统之间的模型，并回答之前的问题，我们可以考虑以下关系：

七鳃鳗数量与生态系统中的食物链关系：七鳃鳗作为捕食者和被捕食者，其数量会受到食物资源的影响。
七鳃鳗数量与生态系统中其他物种的数量和分布：七鳃鳗的数量变化可能会影响其捕食者和被捕食者的数量，从而影响生态系统的平衡。
七鳃鳗数量与生态系统的稳定性：七鳃鳗数量的增加或减少可能会引起生态系统中的扰动，从而影响其稳定性。

基于这些关系，我们可以建立一个简单的数学模型来描述七鳃鳗数量与更大生态系统之间的关系。我们用 $N$ 表示七鳃鳗的总数， $F$ 表示雌性七鳃鳗的数量， $M$ 表示雄性七鳃鳗的数量， $O$ 表示其他生物群体的数量， $S$ 表示生态系统的稳定性。

我们可以使用以下方程来描述这些变量之间的关系：

七鳃鳗数量变化：
$\frac{ {dN}}{ {dt}} = \text{出生率} – \text{死亡率}$
七鳃鳗数量与其他物种数量的关系：
$\frac{ {dO}}{ {dt}} = \alpha \cdot N – \beta \cdot O$
生态系统的稳定性与七鳃鳗数量的关系：
$\frac{ {dS}}{ {dt}} = \gamma \cdot (\text{七鳃鳗数量变化})$

在这些方程中， $\alpha$ 表示七鳃鳗对其他物种数量的影响系数， $\beta$ 表示其他物种对七鳃鳗数量的影响系数， $\gamma$ 表示七鳃鳗数量对生态系统稳定性的影响系数。

要建立生态系统的稳定性与七鳃鳗性别比例的变化之间的关系模型，我们可以考虑以下因素：

七鳃鳗性别比例的变化如何影响其数量和种群结构。
七鳃鳗数量和种群结构如何影响其在食物链中的地位和生态功能。
七鳃鳗在生态系统中的地位和生态功能如何影响生态系统的稳定性。

基于这些因素，我们可以建立一个简化的模型来描述生态系统的稳定性与七鳃鳗性别比例的变化之间的关系。我们用 $S$ 表示生态系统的稳定性， $F$ 表示雌性七鳃鳗的数量， $M$ 表示雄性七鳃鳗的数量。

我们可以假设生态系统的稳定性受到七鳃鳗数量和种群结构的影响，其中七鳃鳗数量和种群结构又受到性别比例的影响。我们可以使用以下方程来描述这些变量之间的关系：

$\frac{ {dS}}{ {dt}} = \alpha \cdot \left(\frac{ {d(F – M)}}{ {dt}}\right)$
在这个方程中， $\alpha$ $ 表示七鳃鳗数量和种群结构对生态系统稳定性的影响系数。 $d (F - M) / d t$ 表示雌性七鳃鳗数量和雄性七鳃鳗数量的变化率，即性别比例的变化率。

目前已完成问题1-问题4的进阶代码编写，

问题1代码

import numpy as np 
import matplotlib.pyplot as plt 
 
# 模型参数 
alpha = 0.1  # 雄性相对于资源的生长率 
beta = 0.05  # 雄性相对于数量的死亡率 
gamma = 0.08  # 雌性相对于资源的生长率 
delta = 0.03  # 雌性相对于数量的死亡率 
 
# 初始条件 
M_0 = 100  # 初始雄性数量 
F_0 = 100  # 初始雌性数量 
P_0 = M_0 + F_0  # 初始总体数量 
R_0 = 0.5  # 初始资源可用性 
 
# 模拟时间参数 
dt = 0.1  # 时间步长 
t_max = 100  # 模拟时间 
num_steps = int(t_max / dt) + 1 
 
# 初始化数组 
time = np.linspace(0, t_max, num_steps) 
M = np.zeros(num_steps) 
F = np.zeros(num_steps) 
P = np.zeros(num_steps) 
R = np.zeros(num_steps) 
 
# 设置初始条件 
M[0] = M_0 
F[0] = F_0 
P[0] = P_0 
R[0] = R_0 
 
# Euler 方法求解微分方程 
for i in range(1, num_steps): 
    dM_dt = alpha * R[i-1] - beta * M[i-1] 
    dF_dt = gamma * R[i-1] - delta * F[i-1] 
    dP_dt = dM_dt + dF_dt 
 
    M[i] = M[i-1] + dt * dM_dt 
    F[i] = F[i-1] + dt * dF_dt 
    P[i] = P[i-1] + dt * dP_dt 
    R[i] = R[i-1]  # 在这个简单的模型中，我们假设资源可用性保持不变 
 
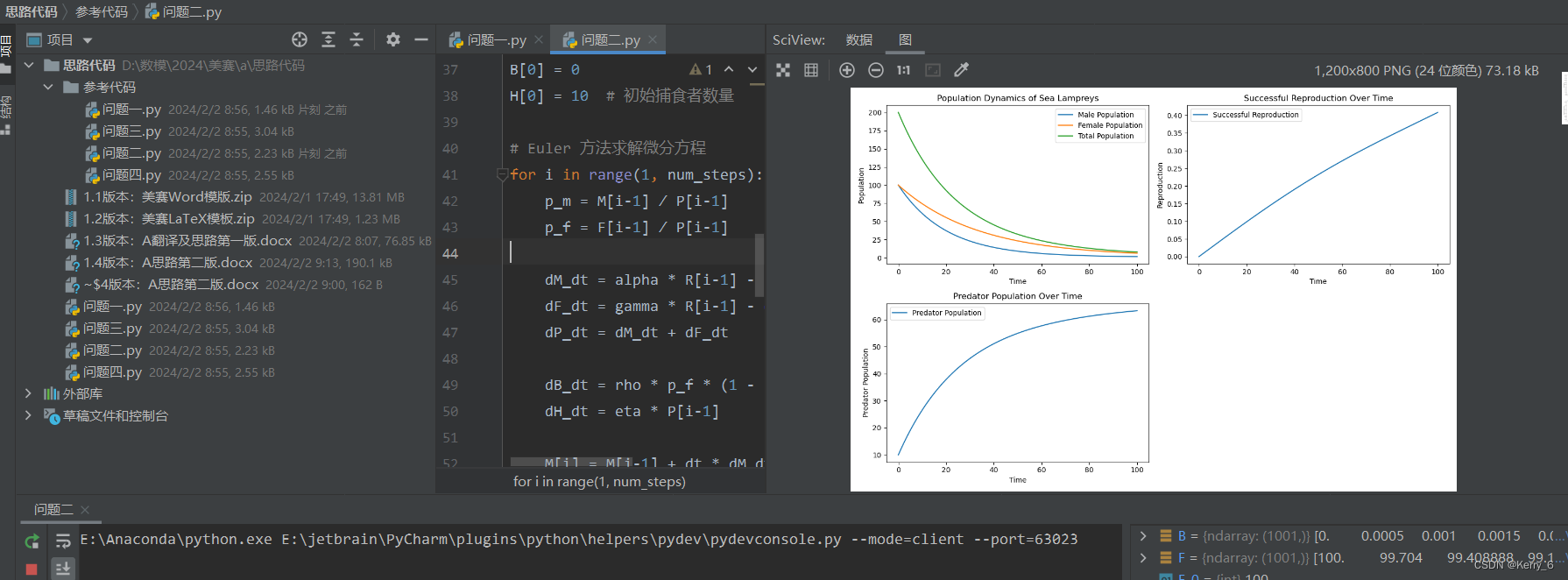
# 绘制结果 
plt.figure(figsize=(10, 6)) 
plt.plot(time, M, label='Male Population') 
plt.plot(time, F, label='Female Population') 
plt.plot(time, P, label='Total Population') 
plt.xlabel('Time') 
plt.ylabel('Population') 
plt.legend() 
plt.title('Population Dynamics of Sea Lampreys') 
plt.show()