广义线性模型是用来做什么的_广义线性模型与一般线性模型的区别「建议收藏」

一、介绍

   广义线性模型 （GLM） 是一个强大的统计框架，它扩展了经典线性回归模型以处理各种数据类型和分布。1970 年代，统计学家 John Nelder 和 Robert Wedderburn 引入了 GLM，已成为从流行病学和金融学到生态学和社会科学等领域不可或缺的工具。本文全面概述了 GLM，探讨了它们的基本概念、关键组件和实际应用。
​

在数据领域，环境和挑战一样多样化，广义线性模型就像多功能指南针，引导我们完成统计建模的复杂领域。GLM 具有适应性强，能够适应各种数据分布，是从最复杂和最多样化的数据集中获取见解的关键，确保没有统计挑战悬而未决。
  

二、GLM的基础

   以线性回归为起点：传统的线性回归模型假设因变量（响应）和自变量（预测变量）之间存在线性关系。这适用于具有恒定方差的连续、正态分布数据。然而，真实世界的数据往往偏离这些假设。
泛化的必要性：GLM 的出现是对线性回归局限性的回应。它们提供了一个更灵活的框架，允许响应变量遵循更广泛的概率分布，包括连续和离散数据。

三、GLM 的关键组件

1. 响应变量分布：GLM 的第一个关键组成部分是响应变量的概率分布选择。常见的分布包括：

• 连续数据的正态（高斯）。
• 二进制或分类数据的二项式。
• 计数数据的泊松。
• Gamma 表示非负连续数据。

2. 链接函数：GLM 包含一个链接函数，该函数将预测变量的线性组合与响应变量的期望值相关联。链接函数的选择取决于响应变量的分布。常用的链接函数包括 identity、logit、log-link 和 inverse-link。
3. 系统组件：GLM 的系统组件由线性预测变量组成，线性预测变量将自变量与其相关系数组合在一起。此组件有助于对预测变量和响应变量之间的关系进行建模。
4. 离散参数：与线性回归不同，GLM 考虑了响应变量中不同程度的离散。在处理表现出异方差性或过度离散的数据时，这一点至关重要，因为它允许更准确的建模。

四、估算方法

   GLM 通常使用最大似然估计 （MLE） 或其他迭代优化技术来估计模型参数。MLE 旨在找到在假设的概率分布下观察给定数据的可能性最大化的参数值。

五、GLM的应用

   回归：GLM 最著名的应用之一是逻辑回归。它用于二元分类问题，其中响应变量表示二元结果（例如，成功或失败，是或否）。logit 链接函数通常用于逻辑回归。
   泊松回归：泊松回归适用于计数数据，例如十字路口的事故数或到达商店的顾客数。它假定响应变量的泊松分布，并采用对数链接函数。
   Gamma 回归：当响应变量为非负且右偏时（例如医疗保健成本或响应时间），则使用 Gamma 回归。在此上下文中使用了 gamma 分布和适当的链接函数。
   其他应用：GLM在各个领域都有应用，包括流行病学（模拟疾病发生）、金融（信用风险建模）、生物学（物种分布建模）和社会科学（调查数据分析）等。

六、代码

   下面是一个完整的 Python 代码示例，演示了如何使用 statsmodels 库创建广义线性模型 (GLM)、生成合成数据集、拟合模型以及使用 matplotlib 绘制结果。我们将使用泊松回归模型作为示例：

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# Create a synthetic dataset
np.random.seed(42)
n_samples = 100
X = np.random.rand(n_samples, 2)  # Two independent variables
# Simulate a Poisson-distributed response variable
lambda_values = np.exp(1 + 2 * X[:, 0] - 1 * X[:, 1])
y = np.random.poisson(lambda_values)

# Create a DataFrame for the dataset
data = pd.DataFrame({ 
   'X1': X[:, 0], 'X2': X[:, 1], 'Y': y})

# Fit a Poisson regression model using GLM
X = sm.add_constant(X)  # Add an intercept term
model = sm.GLM(y, X, family=sm.families.Poisson())
result = model.fit()

# Print the summary of the GLM
print(result.summary())

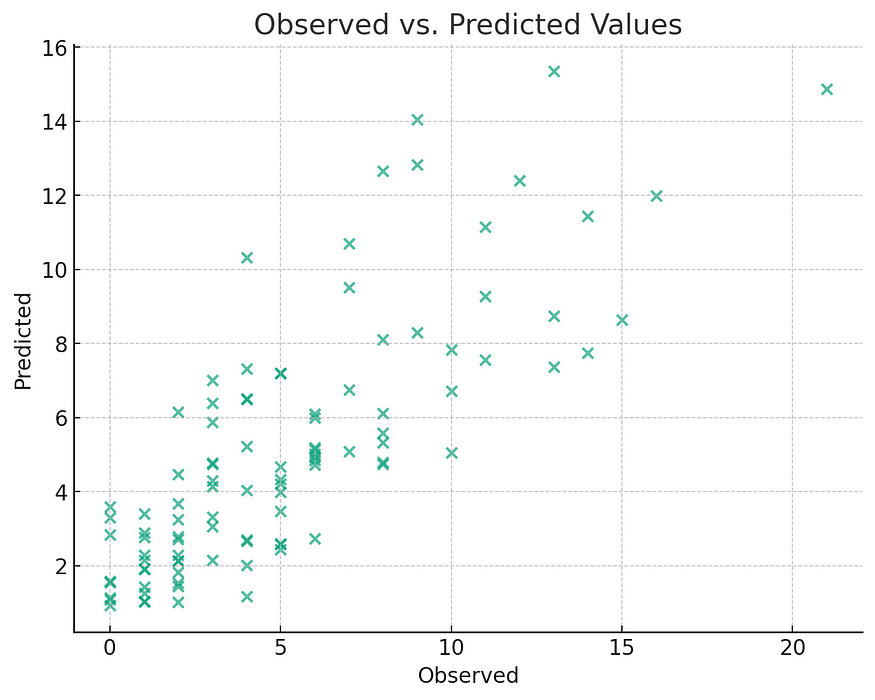
# Plot the observed vs. predicted values
predicted = result.predict(X)
plt.scatter(y, predicted)
plt.xlabel("Observed")
plt.ylabel("Predicted")
plt.title("Observed vs. Predicted Values")
plt.show()

​在此代码中：

1. 我们导入必要的库，包括 NumPy、pandas 、statsmodels和 Matplotlib。
2. 我们生成了一个包含两个自变量（X1 和 X2）和一个泊松分布响应变量 （Y） 的合成数据集。
3. 我们创建一个 DataFrame 来存储数据集。
4. 我们使用 statsmodels的GLM 拟合 Poisson 回归模型。我们在自变量中添加一个截距项。
5. 我们打印 GLM 的摘要，其中提供了有关模型系数和拟合优度的信息。
6. 最后，我们创建了观测值与预测值的散点图，以可视化模型的性能。
   

在运行此代码之前，请确保您的 Python 环境中安装了所需的库（statsmodels、pandas、numpy 和 matplotlib）

七、结论

   广义线性模型 （GLM） 通过提供灵活的框架来适应各种数据类型和分布，从而彻底改变了统计建模。当数据不符合其假设时，它们为传统的线性回归提供了一种有价值的替代方案。了解 GLM 的组成部分，包括分布选择、链接功能和系统组成部分，对于各个领域的研究人员和数据分析师至关重要。凭借其多功能性和稳健的估计方法，GLM 继续在数据分析和假设检验中发挥关键作用，使研究人员能够更深入地了解复杂的现实世界现象。

今天的文章广义线性模型是用来做什么的_广义线性模型与一般线性模型的区别「建议收藏」分享到此就结束了，感谢您的阅读。