数学裂项相消法公式_裂项相消法例题

第二节 裂项相消

(一)、知识呈现

裂项相消法求和也叫拆分法，是指把一个分数拆分成两个或者两个以上分数的相减或相加的形式，然后再进行计算的方法，常有的裂项相消公式有：

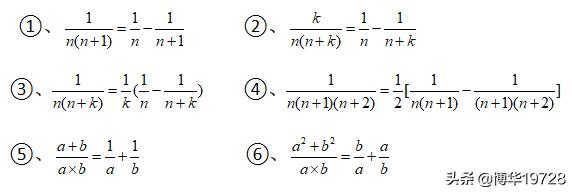
(二)、知识阐释

以①为例讲解一下公式的由来，或者说作一个简单的证明。利用分数通分的逆运算：

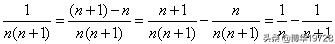
，其余公式的推导大家可以自己进行。

(三)、例题讲解

例1：

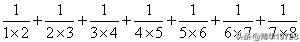
分析与解：观察此题，每项分子都为1，分母为两个连续自然数的乘积，各项之间都是加号相连，分母为两个连续正整数的乘积，因此可以利用公式

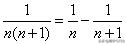
来进行裂项解答。

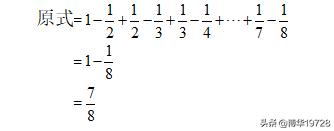
例2：

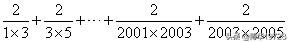
分析与解：此题每项的分子为2，分母为两正整数的乘积，并且两数相差为2，所以可以利用公式

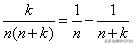
来进行计算，从而达到裂项相消的目的。

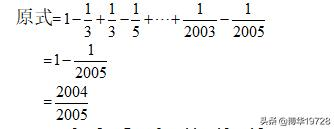
例3：

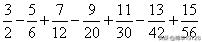
分析与解：观察算式运算符号一减一加，分母能分解成两个连续整数相乘，分子恰为这两个数的和，因此可用公式

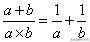
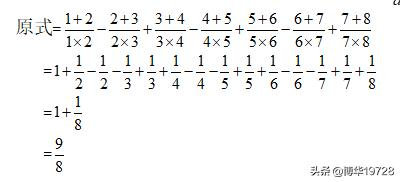
总结：裂项相消法在求有限数列的和中有着广泛的应用，”裂项”是手段，”相消”才是目的，只有实现相消，裂项才有意义，问题才能解决。

本头条号由邹老师主讲中小学数学，通过习题发布，视频讲解，课后巩固三个环节，致力于发展中小学生的数学思维，提高学生的解题能力。欢迎大家关注转发！