深度学习 — Hopfield神经网络详解（吸引子的性质、网络的权值的设计、网络的信息存储容量）

上一节我们详细的讲解了Hopfield神经网络的工作过程，引出了吸引子的概念，简单来说，吸引子就是Hopfield神经网络稳定时其中一个状态，不懂的请看Hopfield神经网络详解，下面我们就开始看看吸引子有什么性质：

1.吸引子的性质

性质1：若是网络的一个吸引子，且阈值 T=0 ，在 sgn(n) 处，，则 (-x) 也一定是该网络的吸引子。

证明：因为是吸引子，即,从而有：

所以 (-x) 也一定是该网络的吸引子。

性质2：若 X^a 是网络的一个吸引子，则与 X^a 的海明距离的 x^b 一定不是吸引子。

注：所谓海明距离是通信的含义就是说状态位不一样的个数，如1100和1000，其海明距离为1，因为不同的位就只有1位，

证明：两个向量的海明距离是指两个向量中不同元素的个数，不妨设

$x_1^a\neq x_1^b,x_j^a\neq x_j^b,j=2,3,...,n$ ,因为 $w_{11}=0$ ,由吸引子定义，有：

$x_1^a = f(\sum_{i=2}^{n}w_{ii}x_i^a - T_1) = f(\sum_{i=2}^{n}w_{ii}x_i^b-T_1)$

由假设条件知， $x_1^a\neq x_1^b$ ,故：

$x_1^b\neq f(\sum_{i=2}^{n}w_{ii}x_i^b-T_1)$

所以 x^b 一定不是吸引子。

性质3：

若有一组向量均是网络的吸引子，且在sgn(0)处，,则有该组向量线性组合而成的向量 $\sum_{p=1}^{P}a_pX^p$ 也是该网络的吸引子。

2.吸引子的吸引域

能使网络稳定在同一吸引子的所有初态的集合，称该吸引子的吸引域，下面给出吸引域的定义：

定义1：若 X^a 是吸引子，对于异步方式，若存在一个调整次序，使网络可以从状态演变到 X^a ，则称弱吸引到 X^a ；若对于任意调整次序，网络都可以从状态演变到 X^a ，则称强吸引到 X^a

定义2：若对于某些，有弱吸引到吸引子 X^a ，则称这些的集合为 X^a 的弱吸引域；若对某些，有强吸引到吸引子 X^a ，则称这些的集合为 X^a 的弱吸引域。

欲使反馈网络具有联想能力，每个吸引子应该都具有一定的吸引域，这样这样带噪声和缺失信息的初始样本，网络才能经过动态演变而稳定到某一个吸引子状态，从而实现正确的联想。反馈网络设计的目的就是要使网络能落到期望的稳定点上，并且具有最可能大的吸引域，以增强联想的功能即抗干扰的能力。

下面举个例子来说明是如何联想的：

这里就不画图了，直接从书中截图过来，然后详细讲解：

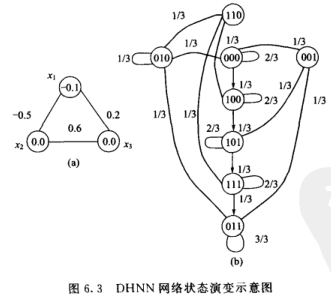
先解释一下，（a）图是说明的权值和阈值，其中圆圈内的是阈值即，连线旁边的是权值，状态的排列是这样的即：,假设的状态的更新顺序为 $x_1\rightarrow x_2\rightarrow x_3$ ,在假设初始状态为000，那么下面开始第一步更新：

设各节点状态取值为1或者0,3节点的DHNN网络应有 2^3 = 8 种状态，设 x = ,更新顺序为： $x_1\rightarrow x_2\rightarrow x_3$ ，下面开始：

第一步更新 x_1 ： $x_1 = sgn[(-0.5)\times 0+0.2\times 0-(-0.1)]=sgn(0.1)=1$ ,其他节点状态不变，网络的状态由变为，如果先更新 x_2 或者 x_3 ,网络状态仍为，因此初始状态保持不变的概率为 $\frac{2}{3}$ ，而变为的概率为 $\frac{1}{3}.$ 。

第二步，此时的网络为，更新 x_2 后，得到 $x_2 = sgn[(-0.5)\times 1+0.6\times 0-0]=sgn(-0.5) = 0,$ 其他节点保持不变，网络状态仍为，如果本步先更新 x_1 或者 x_3 ，网络的状态将为和，因此本状态保持不变的概率为 $\frac{2}{3}$ ，为变为为 $\frac{1}{3}.$ 。

第三步，此时的网络状态为，更新 x_3 得到， $x_3 = sgn(0.2\times 1+0.6\times 0-0) = sgn(0.2)=1$

同理可算出其他状态的直接的演变过程和状态转移概率，如上图b给出八种状态，从图中我们看到是一个吸引子，网络从任意状态更新后都将达到此稳定状态。

上面就是网络的转移过程和联想过程，下面我们来看看，如何设计吸引子，即如何设置网络权值。

3.网络的权值设计

从上面我们知道了网络是如何动态的更新到吸引子的，那么我们现在如何设计吸引子呢？

吸引子的分布是由权值决定的，设计吸引子的核心是如何设计一组合适的权值，为了使所设计的权值满足要求，权值矩阵应符合如下要求：

为保证异步方式工作时网络收敛，应该为对称阵
为保证同步方式工作时网络收敛，应该为非负定对称阵
保证给定的样本是网络的吸引子，并且要有一定的吸引域

根据所要求的的吸引子的数量，可以采用不同的方法设计吸引子，如下：

联立方程法：

下面根据上图的3个节点继续设计吸引子，设要求设计的吸引子为和,权值和阈值在【-1,1】区间取值，试求权值和阈值。

考虑到 $w_{ij} = w_{ji}$ ,对于状态，各节点净输入应该满足如下：

$net_1 = w_{12}\times 1+w_{13}\times 0 - T_1 = w_{12} - T_1 < 0$

0″>

$net_3 = w_{13}\times 0+w_{23}\times 1 - T_3= w_{23} - T_3 < 0$

对于状态，各节点净输入应满足：

0″>

联立可以接得：权值的范围，在范围内选择一个权值就可以，下面直接给出答案了，权值不唯一：

$w_{12}=0.5,T_1 = 0.7$

$w_{13}=0.4,T_1 = -0.2$

$w_{23}=0.5,T_3= 0.1$

因此该参数的从初态最终会演变到我们设计的两个吸引子中。

但是此种方法只适合吸引子较少的时候计算，如果吸引子较多时就需要采用外积和法。

外积和法：

更为通用的权值设计方法是采用Hebb规则的外积和法，设给定P个模式样本 x^p , $p = 1,2,3,,,,,P,x\epsilon \left \{ -1,1 \right \}^n$ ,并且设样本两两正交，且n>p，则权值矩阵为记忆样本的外积和：

$W = \sum_{p=1}^{P}x^p(x^p)^T$ $\left ( 1 \right )$

若 $w_{jj} =0$ ,上式写为：

$W = \sum_{p=1}^{P}[x^p(x^p)^T-I]$ $\left ( 2 \right )$

式中，为单位矩阵，上式写成分量形式，可写为：

$w_{ij} = \left\{\begin{matrix} \sum_{p=1}^{P}x_i^px_j^p, \ i\neq j\ & \\ & \\ & \\ 0, \ i=j\ \end{matrix}\right.$

所以上面w必然满足对称性要求，下面还需要检查一下是否为吸引子。

因P个样本 x^p ， $p = 1,2,3,,,,,P,x\epsilon \left \{ -1,1 \right \}^n$ 是两两正交的，有：

$(x^p)^Tx^k = \left\{\begin{matrix} 0, \ p\neq k\ & \\ & \\ & \\ n, \ p=k\ & \end{matrix}\right.$

所以：

$WX^k = \sum_{p=1}^{P}[x^p(x^p)^T - I]x^k = \sum_{p=1}^{P}[x^p(x^p)^Tx^k-x^k]$

因为n>p,所以有：

可见给定样本 x^p ，是吸引子，但是需要指出来的是我们设计时有时候并不能正好的设计那么多，例如我需要60个吸引子，但是我需要设计64个吸引子，因此会多出4个吸引子，该吸引子称为伪吸引子。下面画个图给大家理解一下什么意思，伪吸引子并不是我们想要的，但是它存在：

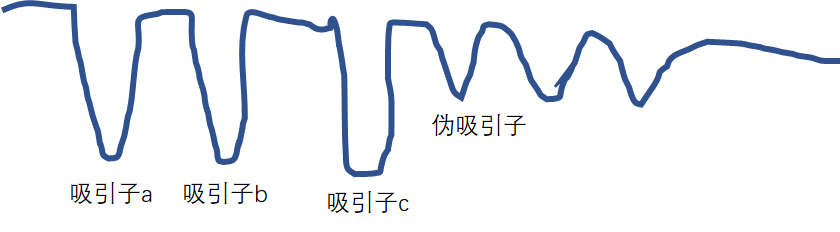
假如吸引子a，b，c是我们设计的吸引子，但是后面的就是伪吸引子，如何处理伪吸引子，我们将在下节继续讨论，这里先提一下。

4.网络的信息存储容量

当网络规模一定时，所能记忆的模式是有限的，对于所容许的联想出错率，网络所能存储的最大模式数 $P_{max}$ 称为网络容量，网络的容量与网络的规模、算法以及记忆模式向量的分布都有关系，下面给出DHNN网络存储容量的有关定理：

定理1：若DHNN网络的规模为n，且权矩阵主对角线元素为0，该网络的信息容量上界为n。

定理2：若P个记忆模式 x^p ， $p = 1,2,3,,,,,P,x\epsilon \left \{ -1,1 \right \}^n$ 是两两正交的，n>p,且权值矩阵按照 $\left ( 1 \right )$ 进行求得，则所有P个记忆模式都是DHNN网 (w,0) 的吸引子.

定理3：若P个记忆模式 x^p ， $p = 1,2,3,,,,,P,x\epsilon \left \{ -1,1 \right \}^n$ 是两两正交的，n>p,且权值矩阵按照 $\left ( 2 \right )$ 进行求得，则所有P个记忆模式都是DHNN网 (w,0) 的吸引子.

从上面的定理可知，当用外积设计DHNN网络时，如果记忆模式都满足两两正交的条件，则规模为n维网络最多可记忆n个模式，一般情况，模式样本不可能都满足正交条件，对于非正交模式，网络的信息存储会大大降低。

事实上，当网络规模n一定时，要记忆的模式越来越多，联想时出错的可能性很大，反之，要求出错率越低，网络的信息存储容量上限越小。研究表明当存储模式数P超过0.15n时，联想时就有可能出错，错误结果对应的是能量的局部极小点，或称为伪吸引子。

提高网络存储容量有两个基本途径：

1.改进网络拓扑结构

2.改进网络的权值设计方法

常用的改进方法有：反复学习法、纠错学习法、移动兴奋门限法、伪逆法、忘记规则和非线性谢谢规则等。

我们们知道了， Hopfield神经网络的最大问题在于伪吸引子的存在，一旦存在伪吸引子，因此容易造成错误，如何处理伪吸引子就是我们下一节所要解决的。

到这里DHNN就结束了，CHNN这里不讲了，感兴趣的自行查阅资料了解。

今天的文章深度学习 — Hopfield神经网络详解（吸引子的性质、网络的权值的设计、网络的信息存储容量）分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/83095.html

深度学习 — Hopfield神经网络详解（吸引子的性质、网络的权值的设计、网络的信息存储容量）

1.吸引子的性质

2.吸引子的吸引域

3.网络的权值设计

4.网络的信息存储容量

相关推荐

发表回复