文章目录
情形一:函数有显式表达式 z = f ( x , y ) z=f(x,y) z=f(x,y)
主要使用函数:meshgrid,mesh,fmesh
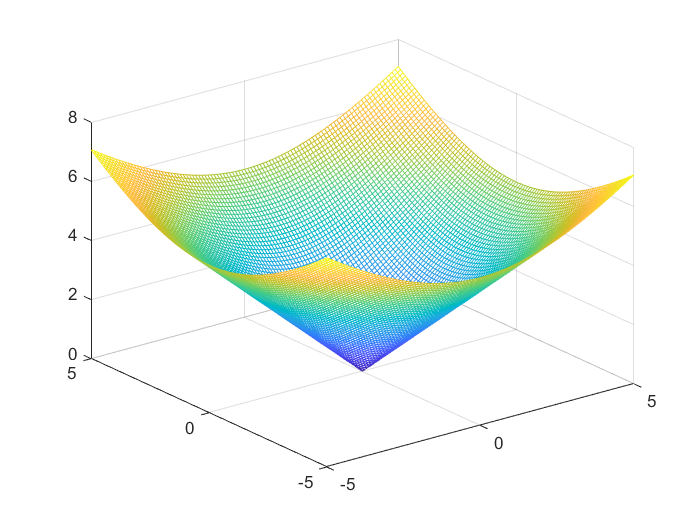
例1:圆锥面: z = x 2 + y 2 z=\sqrt{x^2+y^2} z=x2+y2
clc,clear,close all
x=-5:0.1:5;
[X,Y]=meshgrid(x);
Z=sqrt(X.^2+Y.^2);
mesh(X,Y,Z)
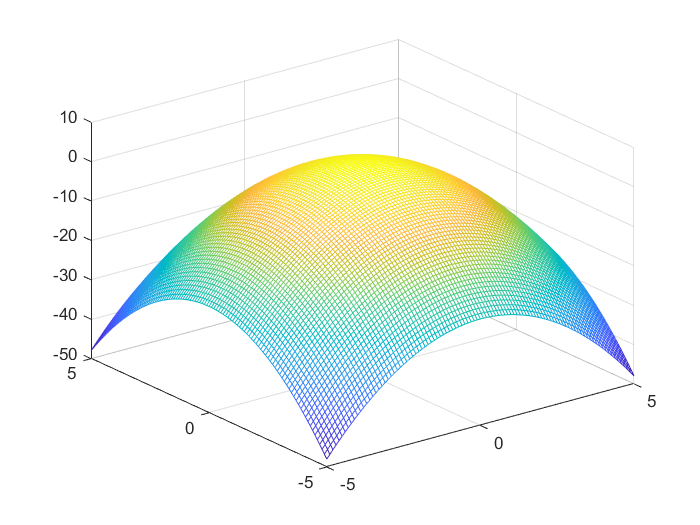
例2:旋转抛物面 z = 2 − x 2 − y 2 z=2-x^2-y^2 z=2−x2−y2
clc,clear,close all
x=-5:0.1:5;
[X,Y]=meshgrid(x);
Z=2-X.^2-Y.^2;
mesh(X,Y,Z)
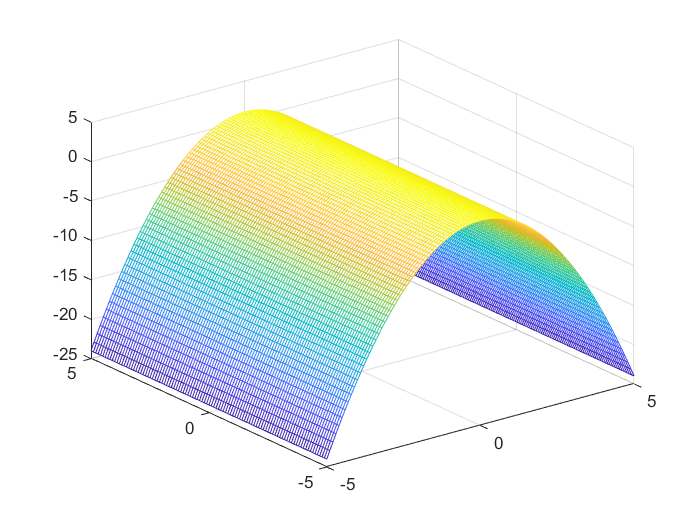
例3:抛物柱面 z = 1 − x 2 z=1-x^2 z=1−x2
clc,clear,close all
x=-5:0.1:5;
[X,Y]=meshgrid(x);
Z=1-X.^2;
mesh(X,Y,Z)
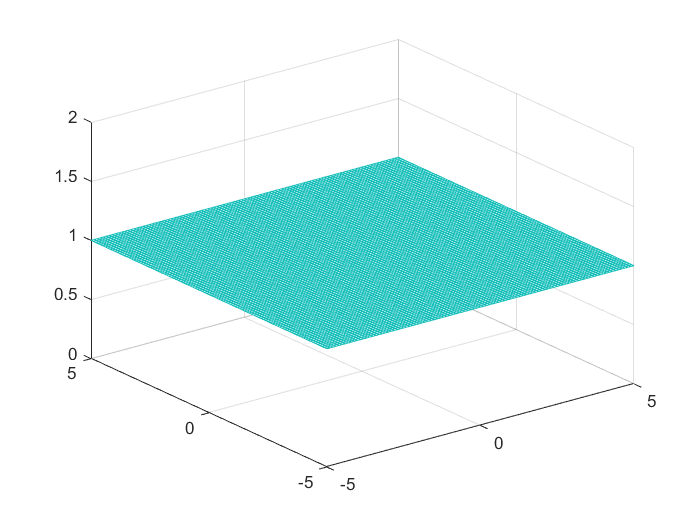
例3:平面 z = 1 z=1 z=1
clc,clear,close all
x=-5:0.1:5;
[X,Y]=meshgrid(x);
Z=zeros(size(X))+1;
mesh(X,Y,Z)
此外,还可利用 fmesh 函数
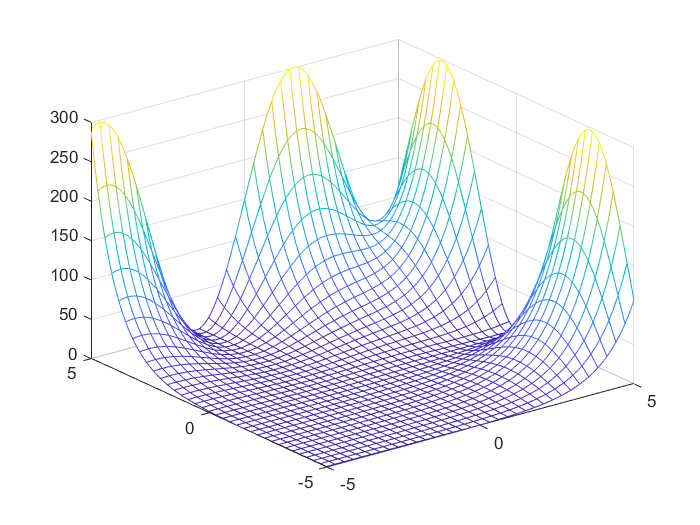
例1: z = e y sin x − e x cos y + e x + e y z=e^y\sin x-e^x\cos y+e^x+e^y z=eysinx−excosy+ex+ey
clc,clear,close all
syms x y
f=sin(x)*exp(y)-cos(y)*exp(x)+exp(x)+exp(y);
fmesh(f)
情形三:函数表达式不含有 z z z 主要使用函数:meshgrid,isosurface
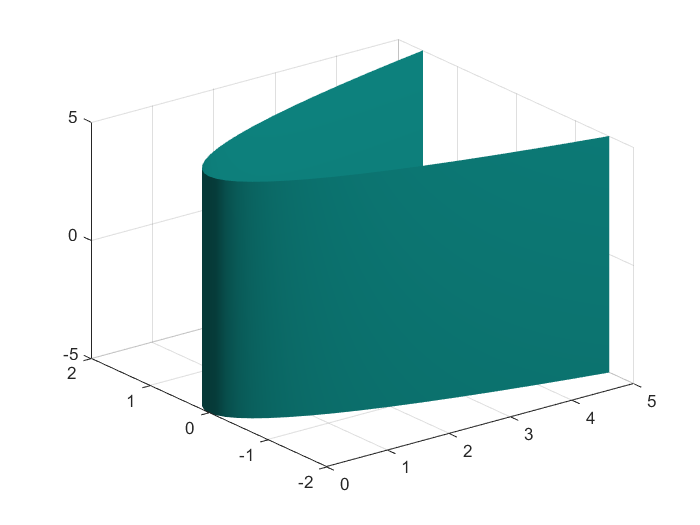
例1:抛物柱面 x = 2 y 2 x=2y^2 x=2y2
clc,clear,close all
x=-5:0.1:5;
y=-5:0.1:5;
z=[-5,5];
[X,Y,Z] = meshgrid(x,y,z);
v = 2*Y.^2-X;
isosurface(X,Y,Z,v,0)
grid on
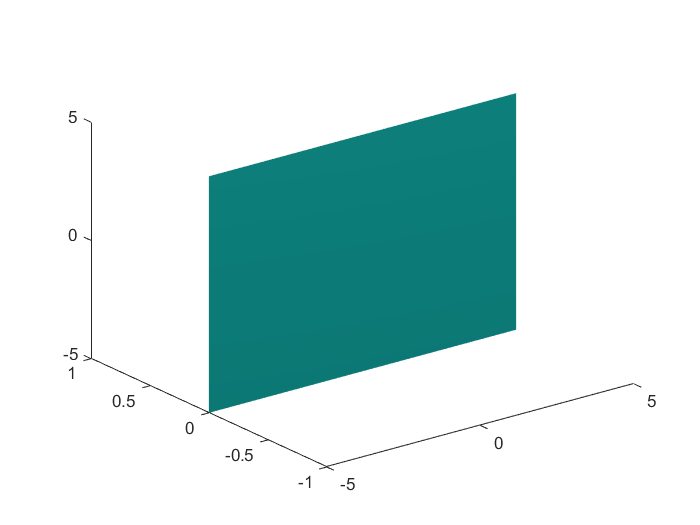
例2:平面 y = 0 y=0 y=0
clc,clear,close all
x=-5:0.1:5;
y=-5:0.1:5;
z=[-5,5];
[X,Y,Z] = meshgrid(x,y,z);
v = Y;
isosurface(X,Y,Z,v,0)
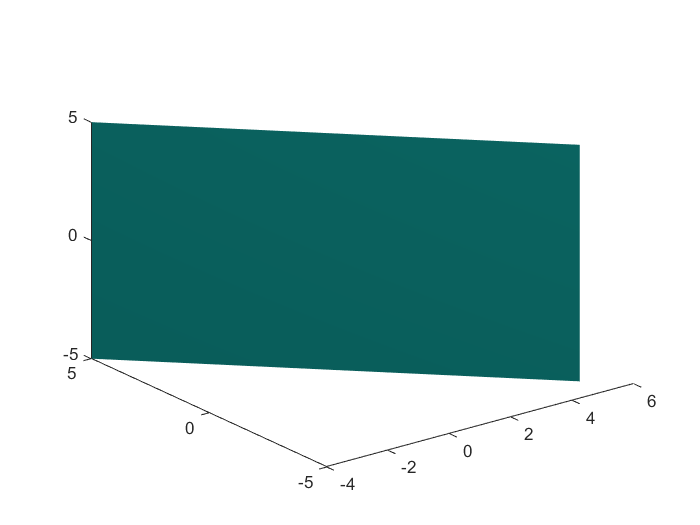
例3:平面 x + y = 0 x+y=0 x+y=0
clc,clear,close all
x=-5:0.1:5;
y=-5:0.1:5;
z=[-5,5];
[X,Y,Z] = meshgrid(x,y,z);
v = X+Y;
isosurface(X,Y,Z,v,0)

情形3:函数有参数表达式
主要使用函数 fplot3
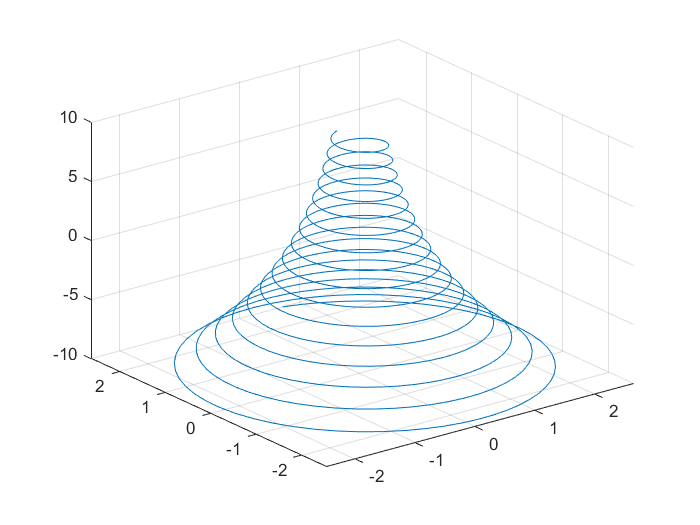
例1:
x = sin ( t ) y = cos ( t ) z = t \begin{aligned} x&=\sin(t)\\ y&=\cos(t)\\ z&=t \end{aligned} xyz=sin(t)=cos(t)=t
clc,clear,close all
xt = @(t) sin(t);
yt = @(t) cos(t);
zt = @(t) t;
fplot3(xt,yt,zt)
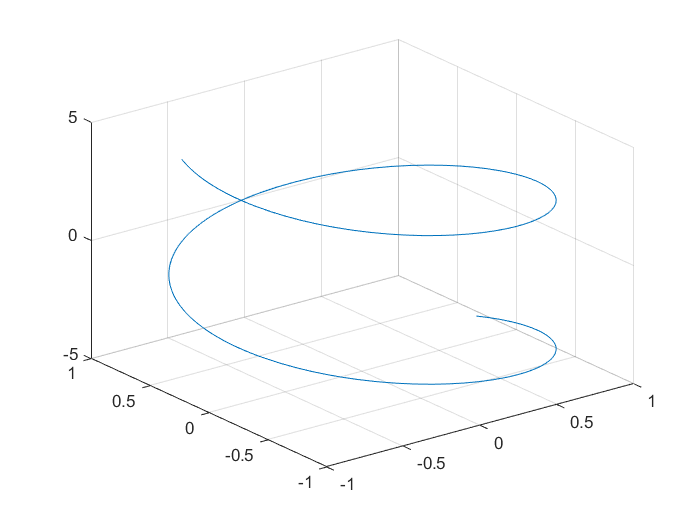
例2:
x = e − t / 10 sin ( 5 t ) y = e − t / 10 cos ( 5 t ) z = t \begin{aligned} x&=e^{-t / 10} \sin (5 t) \\ y&=e^{-t / 10} \cos (5 t) \\ z&=t \end{aligned} xyz=e−t/10sin(5t)=e−t/10cos(5t)=t
clc,clear,close all
xt = @(t) exp(-t/10).*sin(5*t);
yt = @(t) exp(-t/10).*cos(5*t);
zt = @(t) t;
fplot3(xt,yt,zt,[-10 10])
特殊情形1:取定 x , y x,y x,y 后, z z z 的值不唯一
这种情况往往需要分别求出每一个z,然后多次利用 mesh 函数绘图,比较复杂。(也可能有别的方法,但我不是很懂)
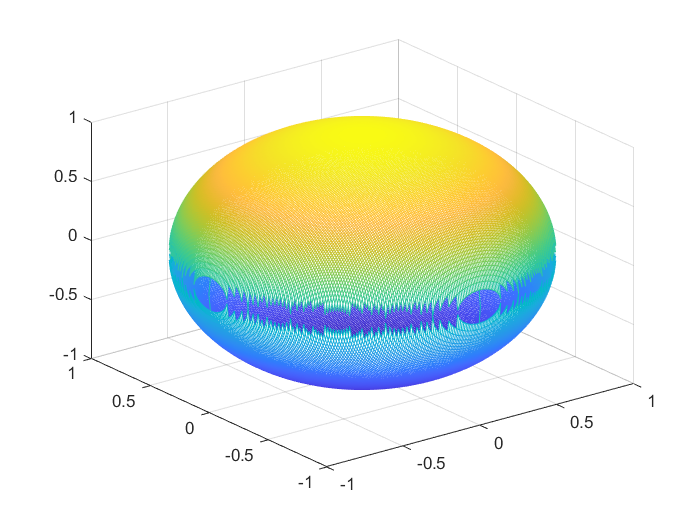
例1: x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1 (此例也可利用参数方程来绘图,此处使用mesh函数仅做示例用,效果并不如fplot3函数好用)
clc,clear,close all
x=-1:0.01:1;
[X,Y]=meshgrid(x);
Z=1-X.^2-Y.^2;
Z(Z<0)=nan; %这一步是为了后面对Z取根号的时候不会得到虚数
Z1=sqrt(Z);
Z2=-sqrt(Z);
mesh(X,Y,Z1)
hold on
mesh(X,Y,Z2)
一个比较复杂的例子
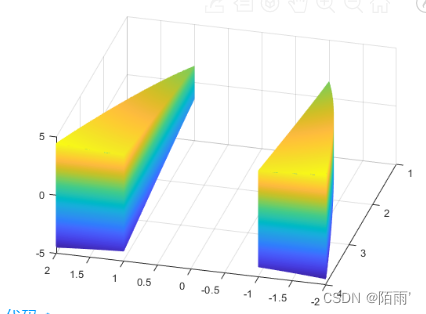
1 ⩽ x 2 ⩽ y < 4 1\leqslant x^2\leqslant y <4 1⩽x2⩽y<4
z 2 ⩽ x 2 + y 2 z^2\leqslant x^2+y^2 z2⩽x2+y2
clc,clear,close all
x = -2:0.01:2;
y = 1:0.01:4;
[X,Y]=meshgrid(x,y);
index1 = X.^2-Y>0;
X(index1) = nan;
Y(index1) = nan;
index2 = X.^2<1;
X(index2) = nan;
Y(index2) = nan;
Z1 = sqrt(X.^2+Y.^2);
mesh(X,Y,Z1)
hold on
Z2 = -sqrt(X.^2+Y.^2);
mesh(X,Y,Z2)
hold on
x = -2:0.01:-1;
z = linspace(-5,5,length(x));
[X,Z] = meshgrid(x,z);
Y = ones(length(x))*4;
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
x = 1:0.01:2;
z = linspace(-5,5,length(x));
[X,Z] = meshgrid(x,z);
Y = ones(length(x))*4;
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
y = 1:0.01:4;
z = linspace(-5,5,length(y));
[Y,Z] = meshgrid(y,z);
X = ones(length(y))*(-1);
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
y = 1:0.01:4;
z = linspace(-5,5,length(y));
[Y,Z] = meshgrid(y,z);
X = ones(length(y))*(1);
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
x = -2:0.01:-1;
z = linspace(-5,5,length(x));
[X,Z] = meshgrid(x,z);
Y = X.^2;
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
x = 1:0.01:2;
z = linspace(-5,5,length(x));
[X,Z] = meshgrid(x,z);
Y = X.^2;
index = Z.^2-X.^2-Y.^2>0;
X(index) = nan;
Y(index) = nan;
Z(index) = nan;
mesh(X,Y,Z)
2022年5月16日18:23:26
今天的文章MATLAB 绘制三维图 | 附多个实例分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/8323.html