今天讲一个在信号分析领域较为常用的一个方法,即盲源分离算法中的FastICA。
我们先从一个经典的问题引入。
一、鸡尾酒舞会问题
想象一下,你身处一个熙熙攘攘的鸡尾酒舞会中。四周回荡着各种声音:笑声、交谈声、玻璃碰撞声,甚至还有远处柔和的爵士乐。这个场景就是所谓的“鸡尾酒舞会问题”的现实写照。
在这个舞会中,每个人都在与他人交流,他们的声音混合在一起,形成了一片难以分辨的嘈杂声。假如你是一个参与者,尽管周围噪音重重,你仍然能够集中注意力,听清楚你对话伙伴的每一个字。但是,对于房间里的录音设备来说,挑战就来了。它捕捉到的是一个复杂的声音混合体,所有的声音都叠加在一起,没有明显的分界线。
鸡尾酒舞会
现在,假设我们的目标是从录音设备捕获的这个声音混合体中,分离出每一个单独的声音源,无论是一个人的谈话声,还是那柔和的背景爵士乐。这就是盲源分离问题的核心,它试图恢复出原始的、独立的声音信号。盲源分离在这种情况下的难度在于,我们事先并不知道声音是如何混合在一起的,也不知道有多少个独立的声音源。
这个问题之所以被称为“鸡尾酒舞会问题”,是因为它非常形象地描绘了在一个充满杂音的环境中,如何分辨和关注单一声音源的挑战。正如在一个真实的鸡尾酒舞会上,尽管周围噪声四起,人们还是能够聚焦于某个特定的对话或声音,盲源分离算法试图模拟这种人类的听觉选择能力,从一团混乱中恢复出清晰的、独立的声音信号。
二、类似于“鸡尾酒舞会”的研究问题
2.1 故障诊断中的多个传感器采样
在工业生产和设备维护中,故障诊断是确保生产安全和提高效率的重要环节。设备上安装有多个传感器,用于实时监控机械的多通道震动参数。这些传感器收集的数据往往是多种故障信号和正常运行信号的混合体。通过应用盲源分离技术,我们可以从这些混合的传感器数据中分离出代表特定故障特征的信号,从而准确地诊断出设备的具体问题。
2.2 语音信号分离
在多人通话、会议记录或在嘈杂环境中的语音识别场景中,语音信号分离技术尤为重要。这些场景中,我们需要从包含多个说话者声音的混合音频信号中分离出每个个体的语音。这种技术的挑战在于,说话者的语音信号可能相互重叠,并且背景噪音的存在进一步增加了分离的难度。利用盲源分离等技术,可以有效地从混合信号中恢复出清晰的单一说话者语音,这对于提高语音识别的准确率、实现高质量的通话记录以及增强听力辅助设备的性能等都至关重要。
三、盲源分离常用工具之FastICA
了解FastICA算法的本质和流程,我们需要深入探讨其数学原理和实现细节。FastICA算法是基于非高斯性最大化原理的独立成分分析方法,旨在从多维观测数据中提取出统计独立的信号源。下面是FastICA算法的详细步骤和相关解释[1]:
变量含义:
x :表示观测信号。在FastICA的框架下, x 是多维观测数据,可以理解为包含多个混合信号的向量。例如,在声音处理的场景中,如果有多个麦克风同时记录多人对话,每个麦克风接收到的声音信号可以组成一个观测向量 x 。
w :表示权重向量。在寻找最大非高斯方向的步骤中, w 用于投影观测数据 x 以提取独立成分。权重向量 w 的方向决定了数据投影的方向,其目的是找到一个方向,使得在这个方向上投影的数据的非高斯性最大。
s :表示独立成分。这是FastICA算法的输出,代表从观测数据 x 中提取出的统计独立的信号。在理想情况下,每个独立成分 s 对应于原始数据源中的一个单独成分,且这些成分之间统计独立。
在FastICA算法的迭代过程中,通过调整权重向量 w 来最大化观测数据 x 在某个方向上投影的非高斯性。当找到最优的 w 后,使用它来计算独立成分
,这里的 x″ 是经过预处理(中心化和白化)后的观测数据。这个过程可以提取出原始混合信号中的独立成分,进而实现信号的分离和特征提取。
步骤 1: 中心化
- 操作: 对每个观测向量 x 计算均值 μ ,然后对所有观测向量进行中心化处理,即 x′=x−μ 。这一步骤确保数据的均值为零,为后续的白化和独立成分提取准备数据。
步骤 2: 白化
- 目的: 白化的目的是将输入数据转换为新的数据集,新数据集中的变量相互独立且具有相同的方差。这是通过消除数据的协方差来实现的,从而简化了后续的独立成分提取过程。
- 操作:
- 计算中心化后数据的协方差矩阵
。
- 对协方差矩阵进行特征值分解
,其中 D 是特征值对角矩阵, E 是对应的特征向量矩阵。
- 使用特征值和特征向量对数据进行变换,得到白化数据。
步骤 3: 寻找最大非高斯方向
- 原理: FastICA的核心在于利用非高斯性最大化原理来提取独立成分。非高斯性是通过非高斯性度量(如峰度或熵的近似)来量化的。在所有具有相同方差的分布中,高斯分布具有最小的非高斯性(即,最大的熵)。
- 操作:
- 初始化: 选择一个随机的单位向量 w 作为权重向量的初始值。
- 固定点迭代更新: 对权重向量 w 应用以下更新规则,直到收敛:
其中, g(⋅) 是非线性函数,用于捕捉非高斯性, g′(⋅) 是其导数。更新后,需要对 w+ 进行归一化。
- 正交化: 如果提取多个独立成分,需要对新的权重向量进行正交化处理,以确保它们相互独立。
步骤 4: 计算独立成分
- 操作: 使用最终得到的权重向量 w 将白化后的数据投影到独立成分上,即
。
步骤 5: 重复对其他成分的提取
- 操作: 重复步骤 3 和步骤 4 来提取更多的独立成分,每次提取时都要确保新的权重向量与之前提取的独立成分正交(或独立)。
四、FastICA的几个重要问题
1.所谓的“非高斯性”指的是什么?
高斯性信号指的是其概率分布遵循高斯分布(正态分布)的信号,而白噪声就是高斯性信号的一种。
许多实际应用中的信号(如语音、图像和生物医学信号)自然地呈现非高斯分布。利用这一特点,可以将混合信号分离为其独立源信号,这是ICA的主要目标之一。
非高斯性可以作为随机变量独立性的一种度量。在ICA中,这意味着通过寻找最大化非高斯性的投影,可以帮助识别出数据中的独立成分。非高斯性可以通过多种方式量化,其中包括:
- 峰度(Kurtosis):峰度是衡量概率分布尖锐程度的统计量。对于高斯分布,峰度为3。峰度大于3的分布称为“超高斯”,表现为尖峰和厚尾;峰度小于3的分布称为“亚高斯”,表现为平坦的峰顶。
- 熵(Entropy)或负熵(Negentropy):熵是度量随机变量不确定性的统计量。相比高斯分布,非高斯分布的熵较低,因此负熵可以作为非高斯性的另一种度量。
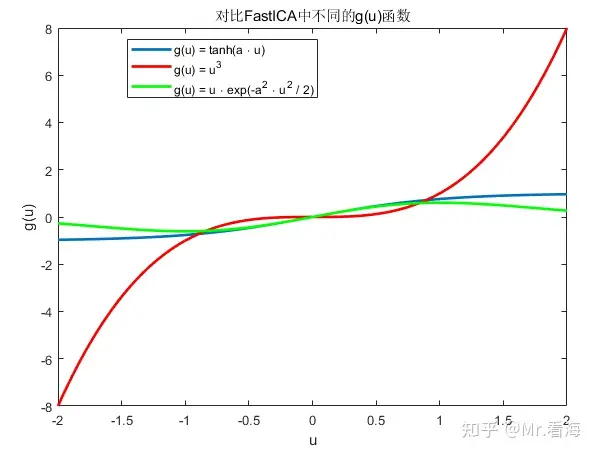
2.非线性函数g(⋅)的作用?
在FastICA算法中,非线性函数g(⋅),常被称为G函数,起着至关重要的作用。它是实现非高斯性最大化的核心,直接影响到算法能够如何以及多么有效地提取出独立成分。
通过选择不同的G函数,FastICA可以适应不同分布类型的源信号。
- 对于超高斯(具有厚尾分布)的信号,通常使用
作为G函数;
- 对于亚高斯(具有尖峰分布)的信号,可以选择
。
- 使用
函数特别适用于那些在零附近有尖峰而在尾部较平坦的分布,因为它通过指数项强化了信号中心部分的贡献,而抑制了远离中心的部分。
这种灵活性允许FastICA处理各种不同的信号类型。、
不图的g(u)曲线图对比
3.关于输出向量排列顺序的不确定性
FastICA算法在提取独立成分时存在一个显著特征,即输出向量(独立成分)的排列顺序具有不确定性。这意味着,当你对同一数据集运行FastICA算法多次时,即使算法每次都成功地分离出了独立成分,这些成分的排列顺序却可能在每次运行之间有所不同。
输出向量排列顺序的不确定性通常不会影响到FastICA算法的有效性和实用性,因为独立成分的物理或统计意义并不依赖于它们的排列顺序。在实际应用中,更关注的是如何准确地识别和解释这些成分,而不是它们的相对位置。
4.关于输出信号幅度的不确定性
FastICA算法在提取独立成分时,除了输出向量排列顺序的不确定性外,还存在输出信号幅度(即独立成分的幅度或标度)的不确定性。这种不确定性源于独立成分分析(ICA)本身的数学性质和FastICA算法的工作原理。下面详细解释这一现象的原因及其对实际应用的影响。
输出信号幅度的不确定性意味着,虽然FastICA能够有效地分离出独立成分,但这些成分的幅度是相对的,而非绝对的。在实际应用中,比较不同数据集的相同独立成分时,不能直接比较它们的幅度。
五、案例演示
下面我们通过案例来演示FastICA的用途及特性。
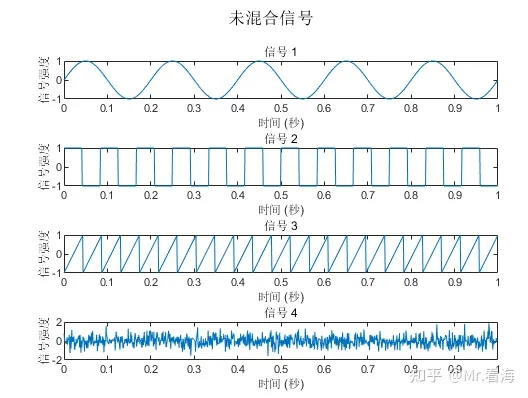
首先通过下边的代码生成正弦、方波、锯齿波、白噪声,然后将他们混合成四组信号。
%% 该程序用于生成仿真信号,并将混合后的信号保存为data.mat文件
% 定义信号长度和采样频率
Fs = 1000; % 采样频率1000Hz
t = 0:1/Fs:1-1/Fs; % 信号总时长为1秒
% 生成测试信号
s1 = sin(2*pi*5*t); % 5Hz的正弦波
s2 = square(2*pi*12*t); % 5Hz的方波
s3 = sawtooth(2*pi*23*t); % 5Hz的锯齿波
s4 = 0.5*randn(size(t)); % 白噪声,振幅缩小一半
% 将信号堆叠成矩阵,每行一个信号
S = [s1; s2; s3; s4];
% 绘制混合信号X的子图
figure('Color','w'); % 创建新图形窗口
for i = 1:size(S, 1)
subplot(size(S, 1), 1, i); % 为每个混合信号指定子图位置
plot(t, S(i, :)); % 绘制每个混合信号
title(['信号 ' num2str(i)]);
xlabel('时间 (秒)');
ylabel('信号强度');
end
% 添加总标题
sgtitle('未混合信号');
% 生成混合矩阵A,这里使用随机矩阵
A = rand(4,4);
% 混合信号
X = A*S;
% 绘制混合信号X的子图
figure('Color','w'); % 创建新图形窗口
for i = 1:size(X, 1)
subplot(size(X, 1), 1, i); % 为每个混合信号指定子图位置
plot(t, X(i, :)); % 绘制每个混合信号
title(['混合信号 ' num2str(i)]);
xlabel('时间 (秒)');
ylabel('信号强度');
end
% 添加总标题
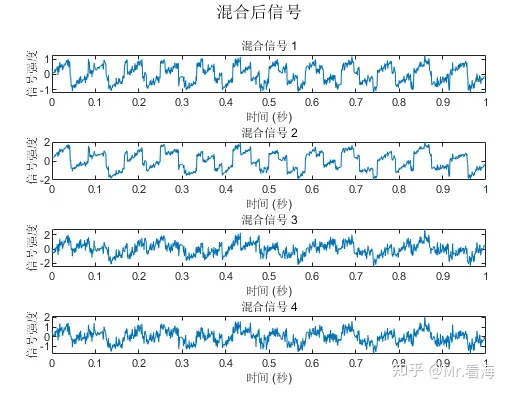
sgtitle('混合后信号');
save data.mat X注意未混合信号的幅值都为1。
下边我们进行FastICA分解,网上可以找到FastICA的工具箱,笔者按照本专栏的惯例对该分解算法进行了傻瓜化的封装,只需要下边三行代码即可:
numOfIC = 0; % 需要提取的独立成分数目,如果不指定数目,则输入0
g = 'pow3'; % 使用的非线性函数类型,可选'pow3', 'tanh', 'gauss', 'skew'
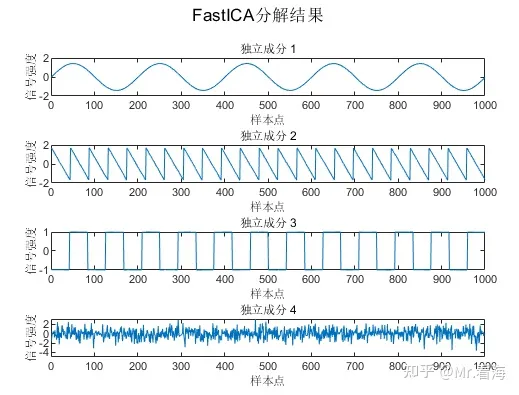
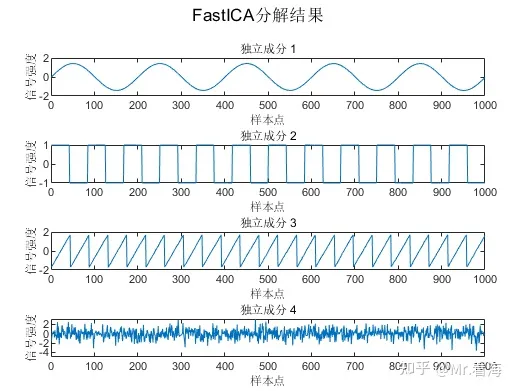
[icasig, A, W] = pFastICA(X, numOfIC, g);可以绘制出以下图像:
此时信号波形已经完美地还原出来,但是需要注意,幅值已经不是原来的幅值了。
现在把同样的程序再运行一遍:
从两次结果对比中可以看出,输出向量排列顺序的不确定性和幅值都是存在不确定性的。
有些同学可能会想对独立成分的频谱进行分析,对此我也封装了绘制各个分量频谱图的函数,像这样调用:
numOfIC = 0; % 需要提取的独立成分数目,如果不指定数目,则输入0
g = 'pow3'; % 使用的非线性函数类型,可选'pow3', 'tanh', 'gauss'
fs = 1000; %采样频率
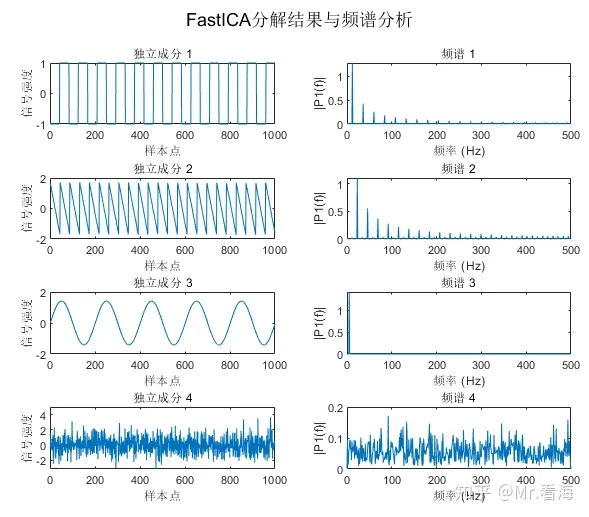
[icasig, A, W] = pFastICAandFFT(X, numOfIC, g,fs);可以得到如下图像:
对于上述两个封装函数,我留出了2个常用的参数。
其一是需要提取的独立成分数目numOfIC,如果不指定数目,则输入0,此时程序会自动判断独立成分数量;也可以指定数目。在上边例子中,我们知道信号由4个独立分量组成,但是如果强制将numOfIC设置为2或者6,会有怎样的结果呢?
我们可以看一下:
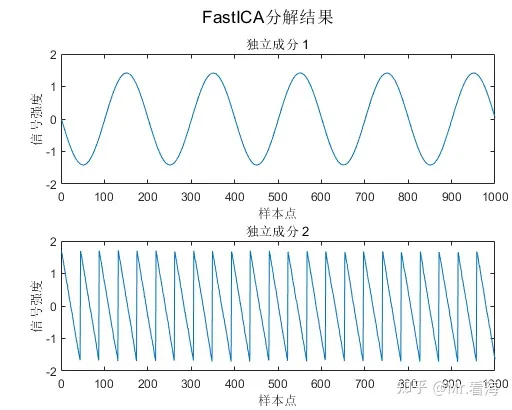
numOfIC设置为2时的结果
numOfIC设置为2时,分解结果为其中的两个独立分量。
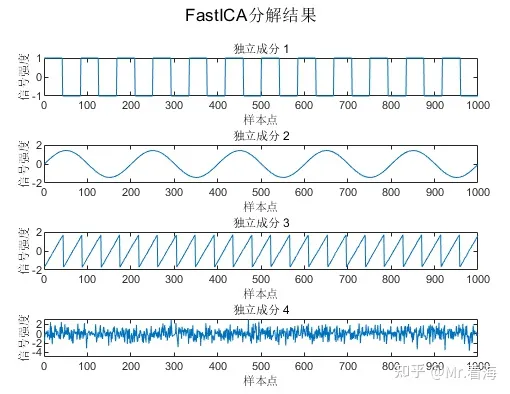
numOfIC设置为2时的结果
numOfIC设置为6时,分解结果为4个独立分量,并不会额外多得到两个分量。
六、FastICA的MATLAB代码实现
其实在上边的案例里已经连带讲到了MATLAB实现,其中我封装了两个绘图函数,其介绍如下:
使用FastICA算法分解混合信号并画图的函数:
function [icasig, A, W] = pFastICA(mixedsig, numOfIC, g)
% pFastICA 使用FastICA算法分解混合信号并画图的代码
% 输入:
% mixedsig - 混合信号矩阵,每行代表一个观测值,每列代表一个观测点
% numOfIC - 需要提取的独立成分数目,如果不指定数目,则输入0
% g - 使用的非线性函数类型,可选'pow3', 'tanh', 'gauss'
% Value of 'g': Nonlinearity used:
% 'pow3' (default) g(u)=u^3
% 'tanh' g(u)=tanh(a1*u)
% 'gauss g(u)=u*exp(-a2*u^2/2)
%
% 输出:
% icasig - 分解后的独立成分信号矩阵
% A - 混合矩阵
% W - 解混矩阵
使用FastICA算法分解混合信号并画图及其频谱的函数:
function [icasig, A, W] = pFastICAandFFT(mixedsig, numOfIC, g, fs)
% pFastICAandFFT 使用FastICA算法分解混合信号并画图及其频谱的代码
% 输入:
% mixedsig - 混合信号矩阵,每行代表一个观测值,每列代表一个观测点
% numOfIC - 需要提取的独立成分数目,如果不指定数目,则输入0
% g - 使用的非线性函数类型,可选'pow3', 'tanh', 'gauss'
% Value of 'g': Nonlinearity used:
% 'pow3' (default) g(u)=u^3
% 'tanh' g(u)=tanh(a1*u)
% 'gauss g(u)=u*exp(-a2*u^2/2)
%
% fs - 采样频率
% 输出:
% icasig - 分解后的独立成分信号矩阵
% A - 混合矩阵
% W - 解混矩阵上述函数不仅可以画出分解图像、频谱图像,也可以导出分解结果和两个矩阵。
其输出变量的计算关系为:
上式中的X就是混合矩阵,也就是函数中的mixedsig变量。
获取代码
上边的测试代码和封装函数,包括工具箱都可以在下边链接,编程不易,感谢支持~
FastICA盲源分离 – 工具箱文档 | 工具箱文档
参考
- ^基于改进的 FastICA 盲源分离研究
今天的文章盲源分离算法研究_基于人工神经网络的盲源分离分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83260.html


 ,这里的 x″ 是经过预处理(中心化和白化)后的观测数据。这个过程可以提取出原始混合信号中的独立成分,进而实现信号的分离和特征提取。
,这里的 x″ 是经过预处理(中心化和白化)后的观测数据。这个过程可以提取出原始混合信号中的独立成分,进而实现信号的分离和特征提取。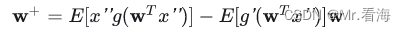 其中, g(⋅) 是非线性函数,用于捕捉非高斯性, g′(⋅) 是其导数。更新后,需要对 w+ 进行归一化。
其中, g(⋅) 是非线性函数,用于捕捉非高斯性, g′(⋅) 是其导数。更新后,需要对 w+ 进行归一化。