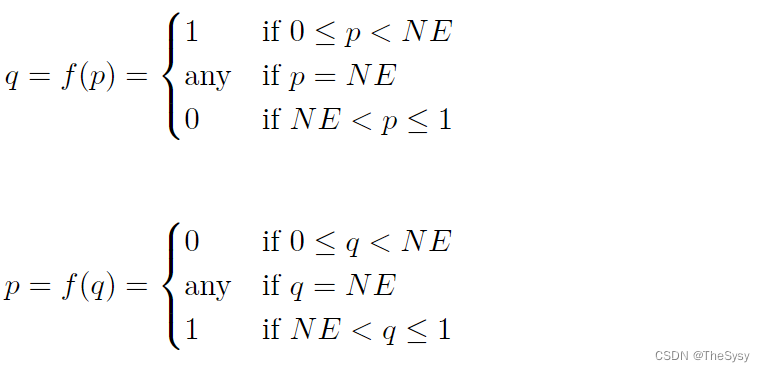上一章中遇到了划线法无法找到均衡的情况,例如盖硬币博弈,盖方盖硬币,猜方猜正反。那是因为考虑的都是纯策略,就是每个策略要么选,要么不选。本章考虑混合策略,就是每个策略都有一个选择的概率。
考虑还是这个盖硬币的博弈,混合策略就是盖方以p的概率盖正,那么就是1-p的概率盖反,猜方同理。p是连续的取值,而如果退化成p只能取1或0,那就退化成原来的纯策略了。
一、寻找纳什均衡
| 策略B1 | 策略B2 | |
| 策略A1 | (2, 3) | (5, 2) |
| 策略A2 | (3, 1) | (1, 5) |
考虑这样一个博弈,均衡就是,给定A的混合策略(p, 1-p),B的混合策略(q, 1-q),双方都不能改变自己的策略来使自己的收益增加。
换句话说,就是给定p,B的任何混合策略的期望都一样,给定q,A的任何混合策略的期望都一样。
这样计算E(B1(p))=E(B2(p))
E(A1(q))=E(B2(q))
解出来就可以得到均衡。
3P+(1-p)=2p+5(1-p)
2p+1=-3p+5
5p=4
P=0.8
2q+5(1-q)=3q+(1-q)
-3q+5=2q+1
-5q=-4
Q=0.8
NE就是{(0.8, 0.2), (0.8, 0.2)}
这里有两个问题
1.为什么这两个纯策略期望一样了,所有的混合策略的期望就都一样了?
考虑混合策略的期望,E=q*E(B1(p)) + (1-q)*E(B2(p)),要对于任意的q,E的值都相等,那是不是只要E(B1(p))=E(B2(p))就好了。
2.这样算出来可能有多个均衡吗,为什么
可能有多个均衡,如果E(B1(p))和E(B2(p))两边的p消了,那取任意的p,这个等式都恒成立了,那任意的p就都是均衡。
二、计算混合策略收益
法一、直接计算
| 策略B1(0.8) | 策略B2(0.2) | |
| 策略A1(0.8) | (2, 3) | (5, 2) |
| 策略A2(0.2) | (3, 1) | (1, 5) |
还是刚才这个例子,均衡之后,每个格子就有自己相应的概率了,每个格子相应的概率乘上对应的人的收益,最后求和就是均衡下这个人的期望收益。
UA=0.8*0.8*2+0.8*0.2*5+0.2*0.8*3+0.2*0.2*1=2.6
UB=0.8*0.8*3+0.8*0.2*2+0.2*0.8*1+0.2*0.2*5=2.6
法二、巧算
既然均衡了,那么就是意味着,A取均衡这一策略,B取任意策略收益都一样,那么我在算B的收益的时候,我就可以固定A为均衡,B的策略取个简单的例如(1, 0),这样可以减少一半的计算,反之亦然。
那么刚才那个每个格子的概率重新写下(算B)
| 策略B1(1) | 策略B2(0) | |
| 策略A1(0.8) | (2, 3) | (5, 2) |
| 策略A2(0.2) | (3, 1) | (1, 5) |
UB=3*0.8+1*0.2=2.6
算A
| 策略B1(0.8) | 策略B2(0.2) | |
| 策略A1(0) | (2, 3) | (5, 2) |
| 策略A2(1) | (3, 1) | (1, 5) |
UA=3*0.8+1*1*0.2=2.6
三、计算混合策略反应函数
这里考虑的是二人博弈,且每人只有两个策略,那么函数就是给定A选择他策略1的概率p,B选择他策略1的概率q应该是多少,所以两个人是两个函数,p=f(q), q=f(p)
二人博弈所以可以化成二维的图
两个策略所以期望是1次函数,不消掉概率的情况下只有一个均衡。
那么满足这两个条件,这类博弈的反应函数就都可以表示为分段函数
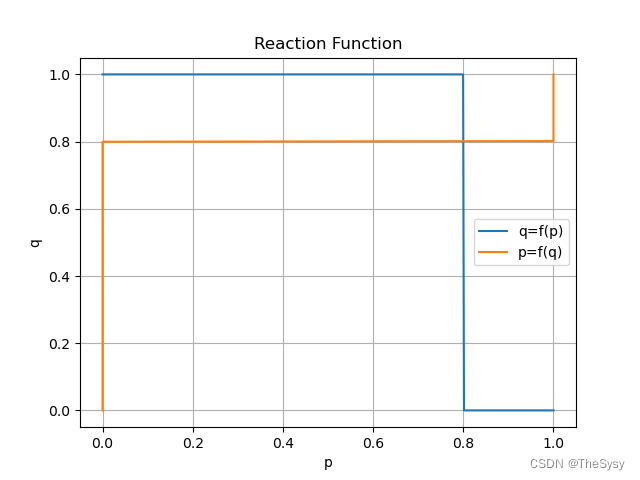
把两个分段函数画在一张图,刚才的例子
定理:反应函数交点是纳什均衡,这是充要条件。
下面附画图python代码
import matplotlib.pyplot as plt
import numpy as np
NEp=0.8
NEq=0.8
# 创建一个细分的p和q值数组
p_values = np.linspace(0, 1, 500)
q_values = np.linspace(0, 1, 500)
# 初始化Q(p)和p(q)的值
Q_values = np.where(p_values < NEp, 1, np.nan)
Q_values = np.where(p_values > NEp, 0, Q_values)
p_q_values = np.where(q_values < NEq, 0, np.nan)
p_q_values = np.where(q_values > NEq, 1, p_q_values)
# 绘制Q(p)
plt.plot(p_values, Q_values, label='q=f(p)')
# 绘制p(q), 并且交换x和y轴的值
plt.plot(p_q_values, q_values, label='p=f(q)')
# 设置图例
plt.legend()
# 设置x和y轴的标签
plt.xlabel('p')
plt.ylabel('q')
# 设置标题
plt.title('Reaction Function')
# 显示网格
plt.grid(True)
# 显示图形
plt.show()今天的文章混合策略纳什均衡一定存在吗_子博弈完美纳什均衡例题分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83446.html