图机器学习(GML)&图神经网络(GNN)原理和代码实现(前置学习系列二）

图机器学习(GML)&图神经网络(GNN)原理和代码实现（PGL）[前置学习系列二]

上一个项目对图相关基础知识进行了详细讲述，下面进图GML

networkx ：NetworkX 是一个 Python 包，用于创建、操作和研究复杂网络的结构、动力学和功能
https://networkx.org/documentation/stable/reference/algorithms/index.html

import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score

1. 图机器学习GML

图学习的主要任务

图学习中包含三种主要的任务：

链接预测（Link prediction）
节点标记预测（Node labeling）
图嵌入（Graph Embedding）

1.1链接预测（Link prediction）

在链接预测中，给定图G，我们的目标是预测新边。例如，当图未被完全观察时，或者当新客户加入平台（例如，新的LinkedIn用户）时，预测未来关系或缺失边是很有用的。

详细阐述一下就是：

GNN链接预测任务，即预测图中两个节点之间的边是否存在。在Social Recommendation，Knowledge Graph Completion等应用中都需要进行链接预测。模型实现上是将链接预测任务看成一个二分类任务：

将图中存在的边作为正样本；
负采样一些图中不存在的边作为负样本；
将正样例和负样例合并划分为训练集和测试集；
可以采用二分类模型的评估指标来评估模型的效果，

例如：AUC值在一些场景下例如大规模推荐系统或信息检索，模型需要评估top-k预测结果的准确性，因此对于链接预测任务还需要一些其他的评估指标来衡量模型最终效果：

MR（MeanRank）
MRR（Mean Reciprocal Rank）
Hit@n

MR, MRR, Hit@n指标含义：假设整个图谱中共n个实体，评估前先进行如下操作：

（1）将一个正确的三元组（h,r,t）中的头实体h或者尾实体t，依次替换成整个图谱中的其他所有实体，这样会产生n个三元组；

（2）对（1）中产生的n个三元组分别计算其能量值，例如在TransE中计算h+r-t的值，这样n个三元组分别对应自己的能量值；

（3）对上述n个三元组按照能量值进行升序排序，记录每个三元组排序后的序号；

（4）对所有正确的三元组都进行上述三步操作MR指标：将整个图谱中每个正确三元组的能量值排序后的序号取平均得到的值；

MRR指标：将整个图谱每个正确三元组的能量排序后的序号倒数取平均得到的值；
Hit@n指标：整个图谱正确三元组的能量排序后序号小于n的三元组所占的比例。因此对于链接预测任务来说，MR指标越小，模型效果越好；
MRR和Hit@n指标越大，模型效果越好。接下来本文将在Cora引文数据集上，预测两篇论文之间是否存在引用关系或被引用关系

新LinkedIn用户的链接预测只是给出它可能认识的人的建议。

在链路预测中，我们只是尝试在节点对之间建立相似性度量，并链接最相似的节点。现在的问题是识别和计算正确的相似性分数！

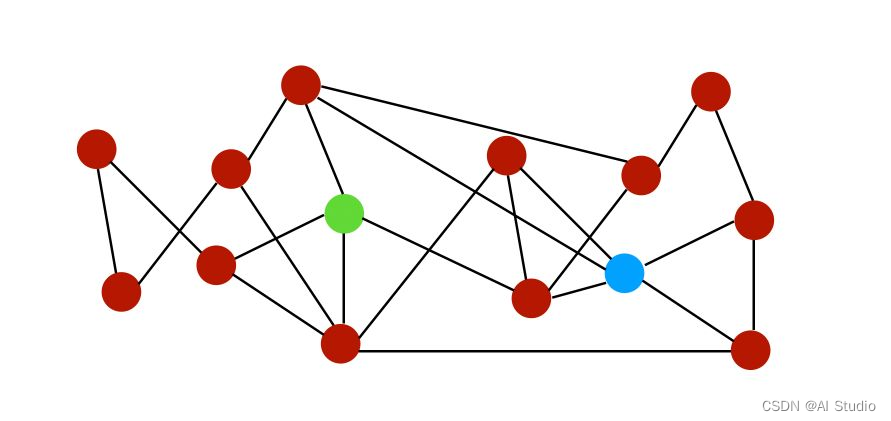
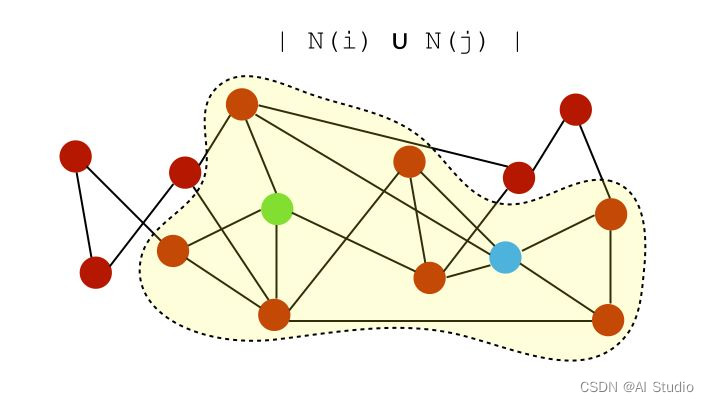
为了说明图中不同链路的相似性差异，让我们通过下面这个图来解释：

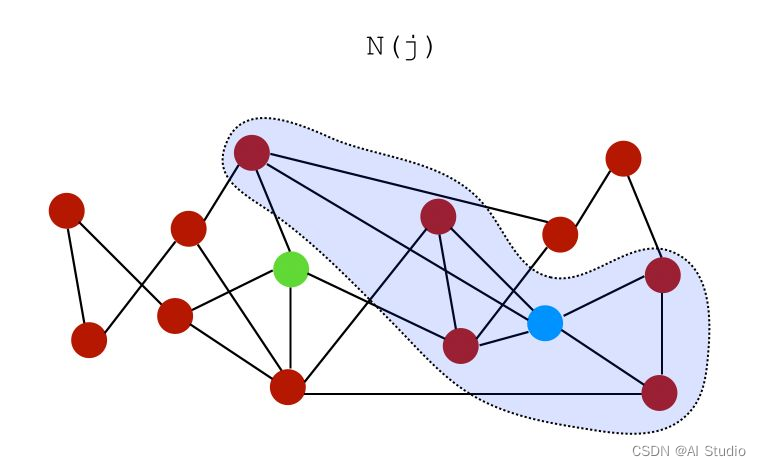
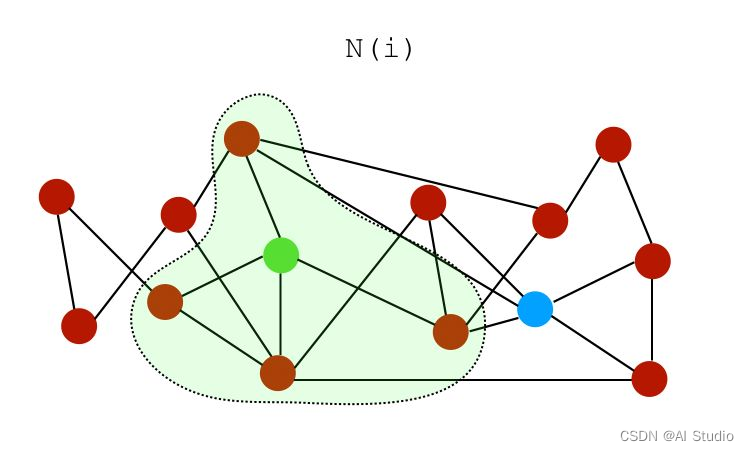
设 $N (i)$ 是节点 $i$ 的一组邻居。在上图中，节点 $i$ 和 $j$ 的邻居可以表示为：

$i$ 的邻居：

1.1.1 相似度分数

我们可以根据它们的邻居为这两个节点建立几个相似度分数。

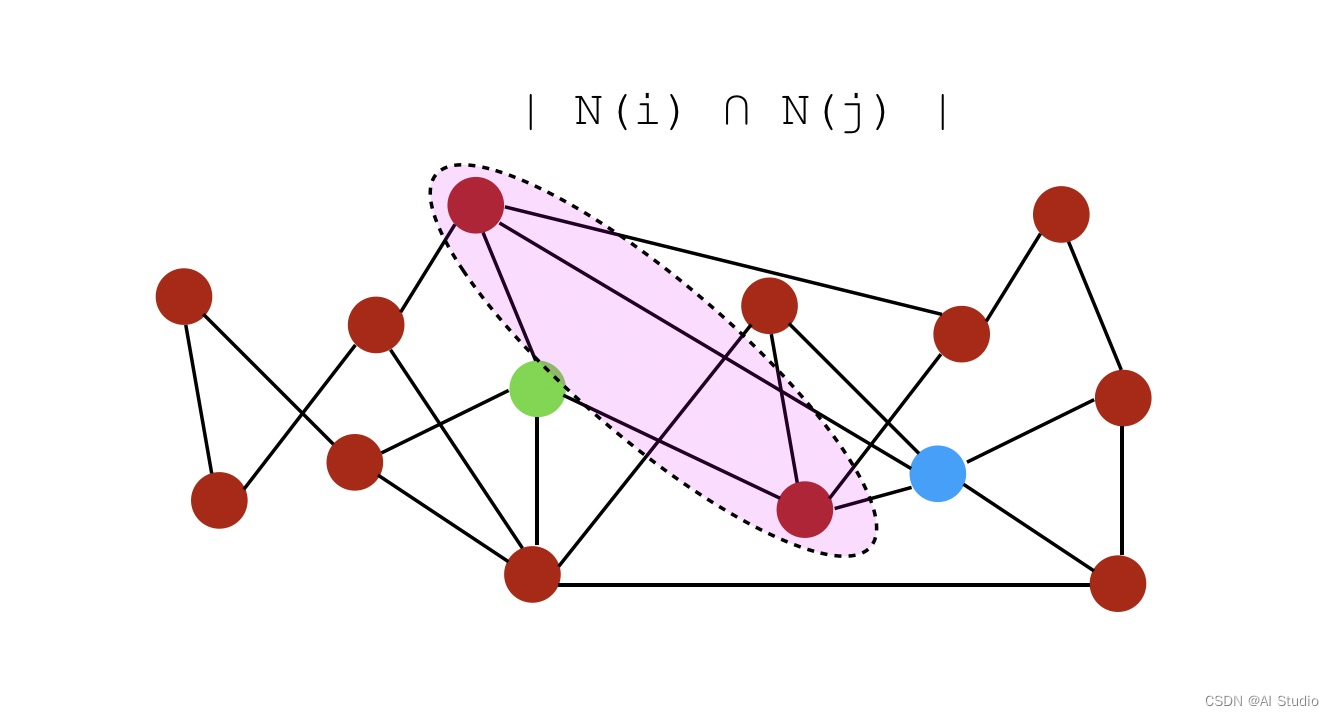
公共邻居： $\mid N(i) \cap N(j) \mid$ ，即公共邻居的数量。在此示例中，分数将为2，因为它们仅共享2个公共邻居。

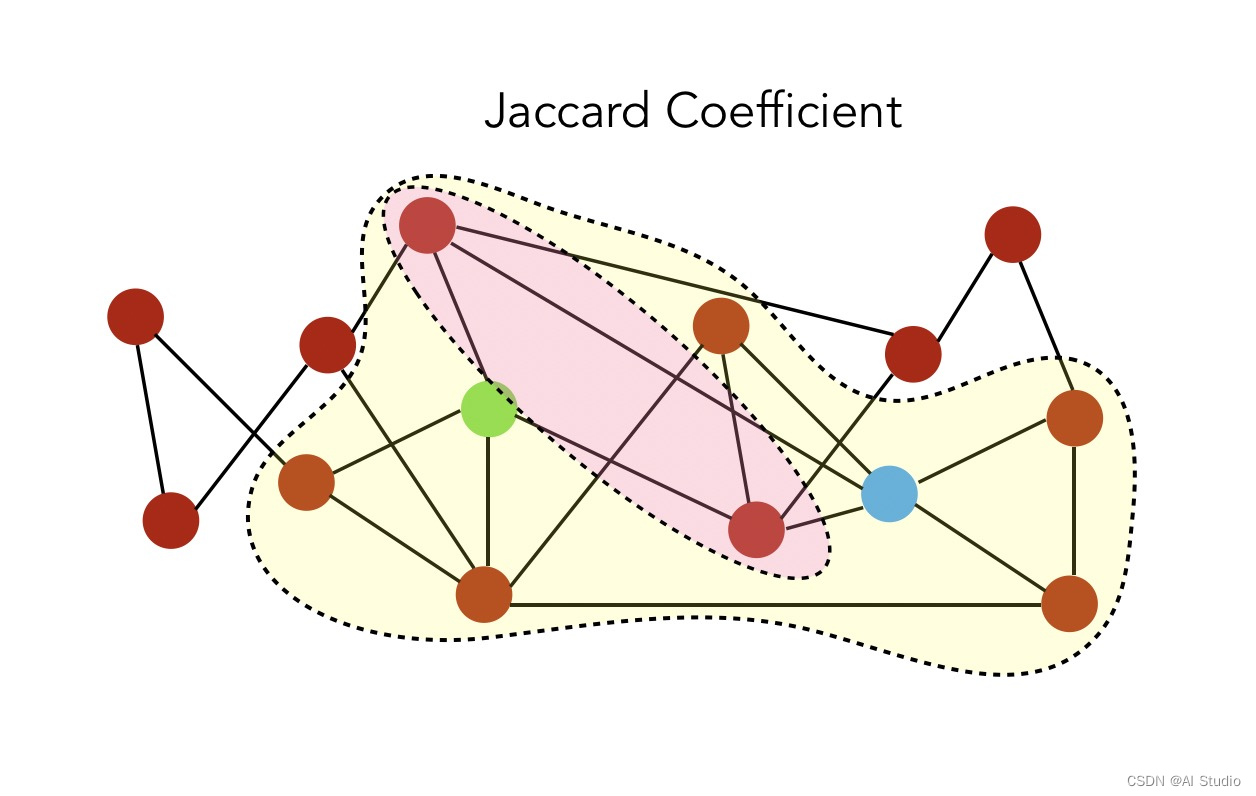
Jaccard系数： $\frac { \mid N(i) \cap N(j) \mid } { \mid N(i) \cup N(j) \mid }$ ,标准化的共同邻居版本。

交集是共同的邻居，并集是：

因此，Jaccard系数由粉红色与黄色的比率计算出：

值是 $\frac {1} {6}$ 。

Adamic-Adar指数： $\sum_{k \in N(i)\cap N(j) } \frac {1} {\log \mid N(k) \mid}$ 。对于节点i和j的每个公共邻居（common neighbor），我们将1除以该节点的邻居总数。这个概念是，当预测两个节点之间的连接时，与少量节点之间共享的元素相比，具有非常大的邻域的公共元素不太重要。
优先依附(Preferential attachment)： $\mid N(i) \mid * \mid N(j) \mid$
当社区信息可用时，我们也可以在社区信息中使用它们。

1.1.2 性能指标(Performance metrics)

我们如何进行链接预测的评估？我们必须隐藏节点对的子集，并根据上面定义的规则预测它们的链接。这相当于监督学习中的train/test的划分。
然后，我们评估密集图的正确预测的比例，或者使用稀疏图的标准曲线下的面积(AUC)。

参考链接：模型评估指标AUC和ROC：https://cloud.tencent.com/developer/article/1508882

1.1.3 代码实践

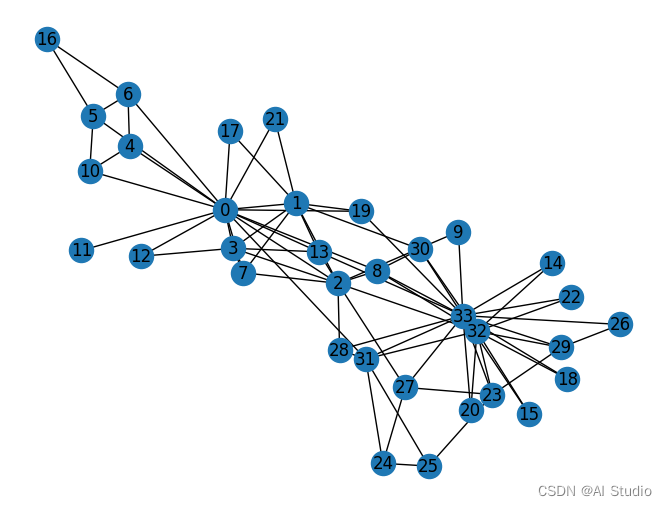
这里继续用空手道俱乐部图来举例：

使用在前两篇文中提及到的Karate图，并使用python来进行实现

# 导入空手道俱乐部图
n=34
m = 78
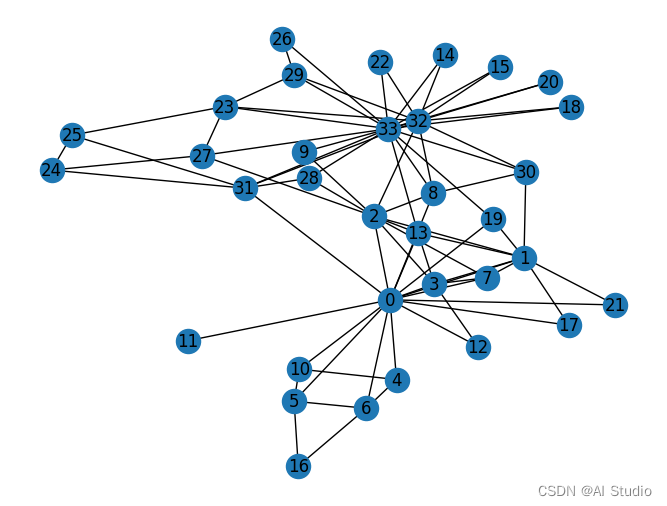
G_karate = nx.karate_club_graph()

pos = nx.spring_layout(G_karate)
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)

# 我们首先把有关图的信息打印出来：
n = G_karate.number_of_nodes()
m = G_karate.number_of_edges()
print("Number of nodes : %d" % n)
print("Number of edges : %d" % m)
print("Number of connected components : %d" % nx.number_connected_components(G_karate))

Number of nodes : 34
Number of edges : 78
Number of connected components : 1

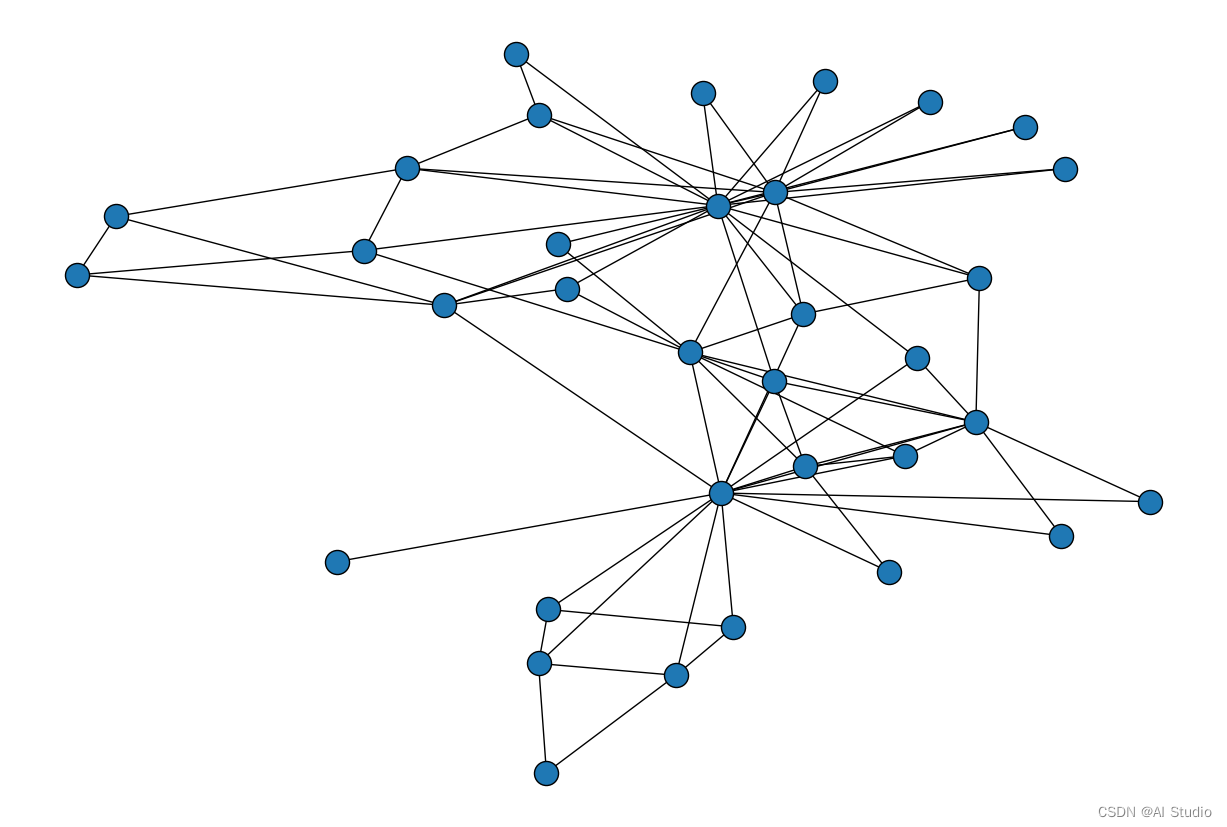
plt.figure(figsize=(12,8))
nx.draw(G_karate, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")

# 现在，让删除一些连接，例如25％的边：
# Take a random sample of edges
edge_subset = random.sample(G_karate.edges(), int(0.25 * G_karate.number_of_edges()))

# remove some edges
G_karate_train = G_karate.copy()
G_karate_train.remove_edges_from(edge_subset)

# 绘制部分观察到的图，可以对比上图发现，去掉了一些边
plt.figure(figsize=(12,8))
nx.draw(G_karate_train, pos=pos)

# 可以打印我们删除的边数和剩余边数：
edge_subset_size = len(list(edge_subset))
print("Deleted : ", str(edge_subset_size))
print("Remaining : ", str((m - edge_subset_size)))

Deleted :  19
Remaining :  59

# Jaccard Coefficient
# 可以先使用Jaccard系数进行预测：
pred_jaccard = list(nx.jaccard_coefficient(G_karate_train))
score_jaccard, label_jaccard = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_jaccard])
# 打印前10组结果
print(pred_jaccard[0:10])
# 预测结果如下，其中第一个是节点，第二个是节点，最后一个是Jaccard分数（用来表示两个节点之间边预测的概率）

[(0, 3, 0.21428571428571427), (0, 7, 0.07142857142857142), (0, 9, 0.07142857142857142), (0, 14, 0.0), (0, 15, 0.0), (0, 16, 0.14285714285714285), (0, 18, 0.0), (0, 20, 0.0), (0, 22, 0.0), (0, 23, 0.0)]

# 然后我们可以使用ROC-AUC标准来比较不同模型的性能，因为我们既有真实的边（label），也有预测边的概率（score）
# Compute the ROC AUC Score
# 其中，FPR是False Positive Rate， TPR是True Positive Rate
fpr_jaccard, tpr_jaccard, _ = roc_curve(label_jaccard, score_jaccard)
auc_jaccard = roc_auc_score(label_jaccard, score_jaccard)
print(auc_jaccard)

0.6277105807998257

# Adamic-Adar
# 现在计算Adamic-Adar指数和对应的ROC-AUC分数
# Prediction using Adamic Adar 
pred_adamic = list(nx.adamic_adar_index(G_karate_train))
score_adamic, label_adamic = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_adamic])
print(pred_adamic[0:10])
# Compute the ROC AUC Score
fpr_adamic, tpr_adamic, _ = roc_curve(label_adamic, score_adamic)
auc_adamic = roc_auc_score(label_adamic, score_adamic)
print(auc_adamic)

[(0, 3, 2.37871300116537), (0, 7, 0.48089834696298783), (0, 9, 0.45511961331341866), (0, 14, 0), (0, 15, 0), (0, 16, 1.8204784532536746), (0, 18, 0), (0, 20, 0), (0, 22, 0), (0, 23, 0)]
0.7000108968072356

# Compute the Preferential Attachment
# 同样，可以计算Preferential Attachment得分和对应的ROC-AUC分数

pred_pref = list(nx.preferential_attachment(G_karate_train))
score_pref, label_pref = zip(*[(s, (u,v) in edge_subset) for (u,v,s) in pred_pref])
print(pred_pref[0:10])
fpr_pref, tpr_pref, _ = roc_curve(label_pref, score_pref)
auc_pref = roc_auc_score(label_pref, score_pref)
print(auc_pref)

[(0, 3, 42), (0, 7, 14), (0, 9, 14), (0, 14, 0), (0, 15, 14), (0, 16, 28), (0, 18, 14), (0, 20, 28), (0, 22, 14), (0, 23, 42)]
0.6276560967636482

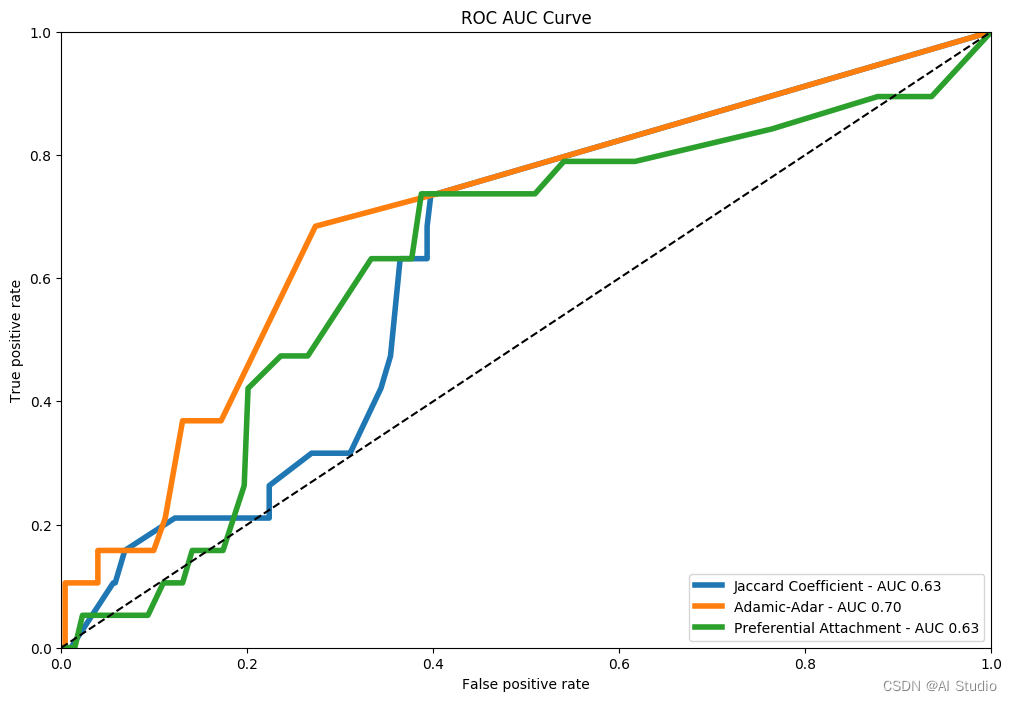
# 绘制ROC-AUC来评价预测的效果
plt.figure(figsize=(12, 8))
plt.plot(fpr_jaccard, tpr_jaccard, label='Jaccard Coefficient - AUC %.2f' % auc_jaccard, linewidth=4)
plt.plot(fpr_adamic, tpr_adamic, label='Adamic-Adar - AUC %.2f' % auc_adamic, linewidth=4)
plt.plot(fpr_pref, tpr_pref, label='Preferential Attachment - AUC %.2f' % auc_pref, linewidth=4)
plt.plot([0, 1], [0, 1], 'k--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title("ROC AUC Curve")
plt.legend(loc='lower right')
plt.show()

1.2 节点标记预测（Node labeling）

给定一个未标记某些节点的图，我们希望对这些节点的标签进行预测。这在某种意义上是一种半监督的学习问题。

处理这些问题的一种常见方法是假设图上有一定的平滑度。平滑度假设指出通过数据上的高密度区域的路径连接的点可能具有相似的标签。这是标签传播算法背后的主要假设。

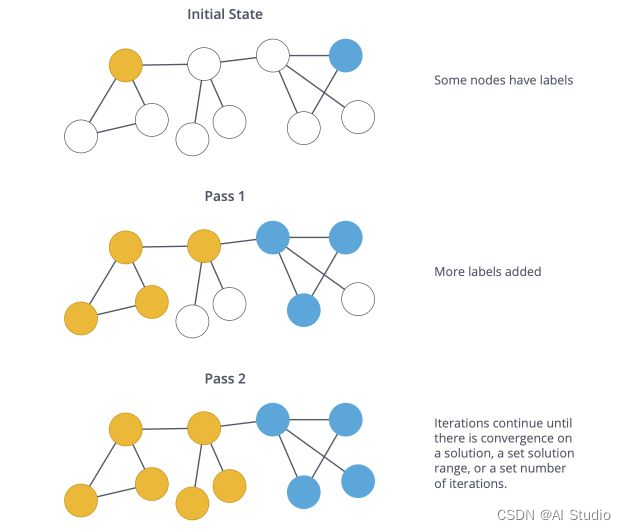
标签传播算法（Label Propagation Algorithm,LPA）是一种快速算法，仅使用网络结构作为指导来发现图中的社区，而无需任何预定义的目标函数或关于社区的先验信息。

单个标签在密集连接的节点组中迅速占据主导地位，但是在穿过稀疏连接区域时会遇到问题。

半监督标签传播算法是如何工作？

首先，我们有一些数据： $x_1, …, x_l, x_{l+1}, …, x_n \in R^p$ ,，以及前 $l$ 个点的标签： $y_1, …, y_l \in 1…C$ .

我们定义初始标签矩阵 $\in R^{n \times C}$ ，如果 $x_i$ 具有标签 $y_i=j$ 则 $Y_{ij} = 1$ ，否则为0。

该算法将生成预测矩阵 $\in R^{n \times C}$ ，我们将在下面详述。然后，我们通过查找最可能的标签来预测节点的标签：

$\hat{Y_i} = argmax_j F_{i,j}$

预测矩阵 $F$ 是什么？

预测矩阵是矩阵 $F^{\star}$ ，其最小化平滑度和准确度。因此，我们的结果在平滑性和准确性之间进行权衡。

问题的描述非常复杂，所以我将不会详细介绍。但是，解决方案是：

$F^{\star} = ( (1-\alpha)I + L_{sym})^{-1} Y$

其中：

参数 $\alpha = \frac {1} {1+\mu}$
$Y$ 是给定的标签
$L_{sym}$ 是图的归一化拉普拉斯矩阵（Laplacian matrix）

如果您想进一步了解这个主题，请关注图函数的平滑度和流形正则化的概念。斯坦福有一套很好的标签图可以下载：https://snap.stanford.edu/data/

Networkx直接实现标签传播：https://networkx.github.io/documentation/latest/reference/algorithms/generated/networkx.algorithms.community.label_propagation.label_propagation_communities.html

接下来我们用python来实现节点标签的预测。
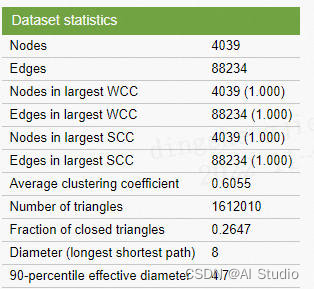
为了给我们使用到的标签添加更多的特征，我们需要使用来自Facebook的真实数据。你可以再这里下载，然后放到facebook路径下。

Facebook 数据已通过将每个用户的 Facebook 内部 id 替换为新值来匿名化。此外，虽然已经提供了来自该数据集的特征向量，但对这些特征的解释却很模糊。例如，如果原始数据集可能包含特征“political=Democratic Party”，则新数据将仅包含“political=anonymized feature 1”。因此，使用匿名数据可以确定两个用户是否具有相同的政治派别，但不能确定他们各自的政治派别代表什么。

我已经把数据集放在目录里了，就不需要下载了

1.2.1 代码实现标签扩散

G_fb = nx.read_edgelist("facebook/3980.edges")
n = G_fb.number_of_nodes()
m = G_fb.number_of_edges()

print("Number of nodes: %d" % n)
print("Number of edges: %d" % m)
print("Number of connected components: %d" % nx.number_connected_components(G_fb))

Number of nodes: 52
Number of edges: 146
Number of connected components: 4

我们使用到的3980号数据，图中有52个节点和146个边。其中，有4个连通分支构成，这意味着这个图中的4块是分开来的。

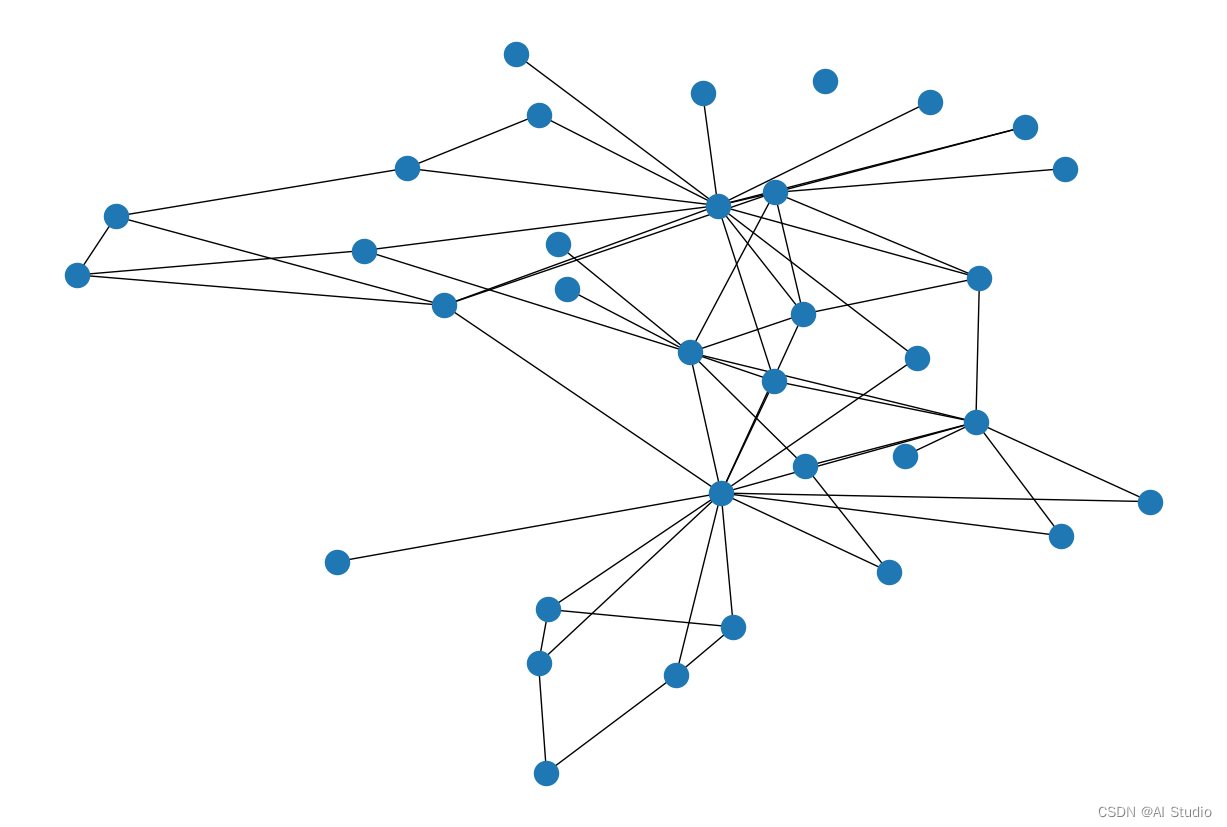
# 我们把图数据显示出来：
mapping=dict(zip(G_fb.nodes(), range(n)))
nx.relabel_nodes(G_fb, mapping, copy=False)
pos = nx.spring_layout(G_fb)

plt.figure(figsize=(12,8))
nx.draw(G_fb, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")

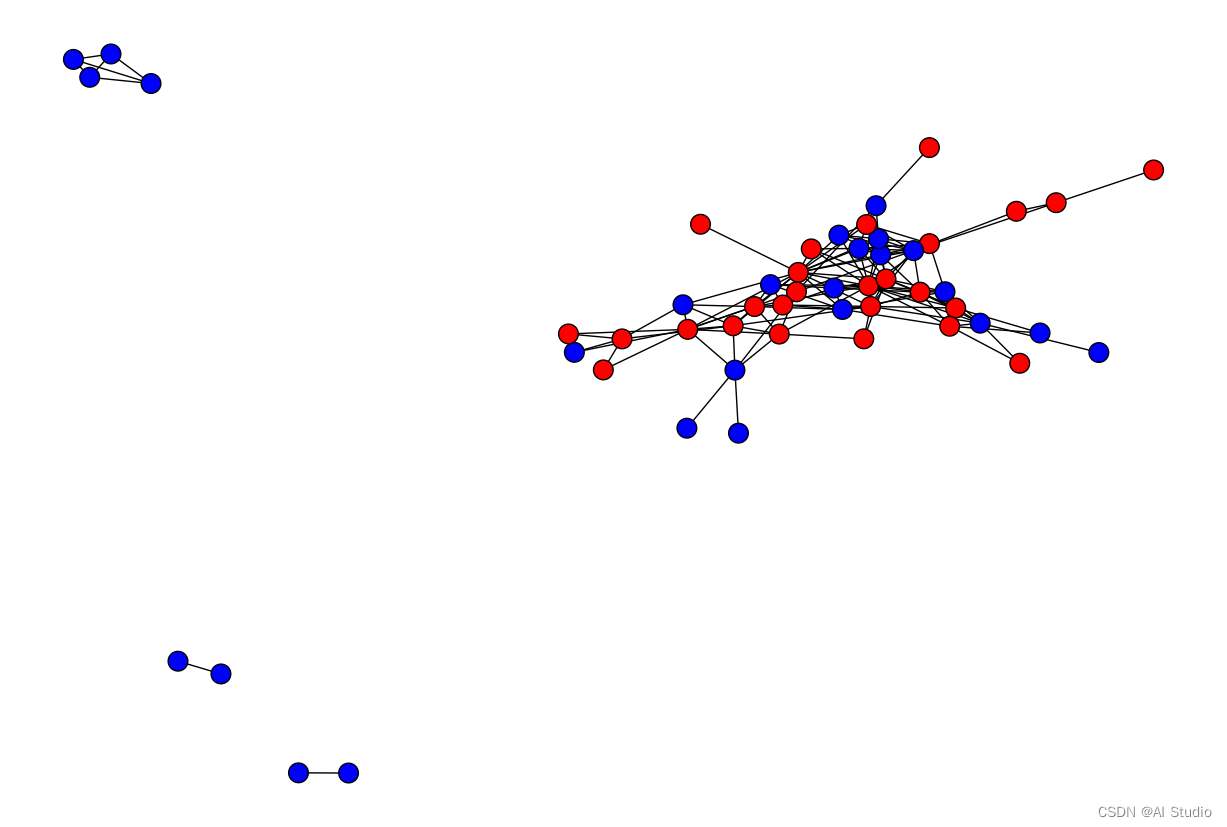
这个图中包含了不同的特征。在这些可用的特征中，我们将利用第34组特征来进行实验。这组特征描述了这个某个facebook用户（节点）是否是一所学校的学生。这里我们两种标签（1是红色的，代表改用户是这所学校的学生，反正，0则用蓝色表示）

with open('facebook/3980.featnames') as f:
    for i, l in enumerate(f):
        pass

n_feat = i+1

features = np.zeros((n, n_feat))
f = open('facebook/3980.feat', 'r')

for line in f:
    if line.split()[0] in mapping:
        node_id = mapping[line.split()[0]]
        features[node_id, :] = list(map(int, line.split()[1:]))

features = 2*features-1
feat_id = 6  #特征选择id，自行设置
labels = features[:, feat_id]

plt.figure(figsize=(12,8))
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = labels, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000")
plt.show()

# 这个所选择的特征，在图中相对平滑，因此拥有较好的学习传播性能。
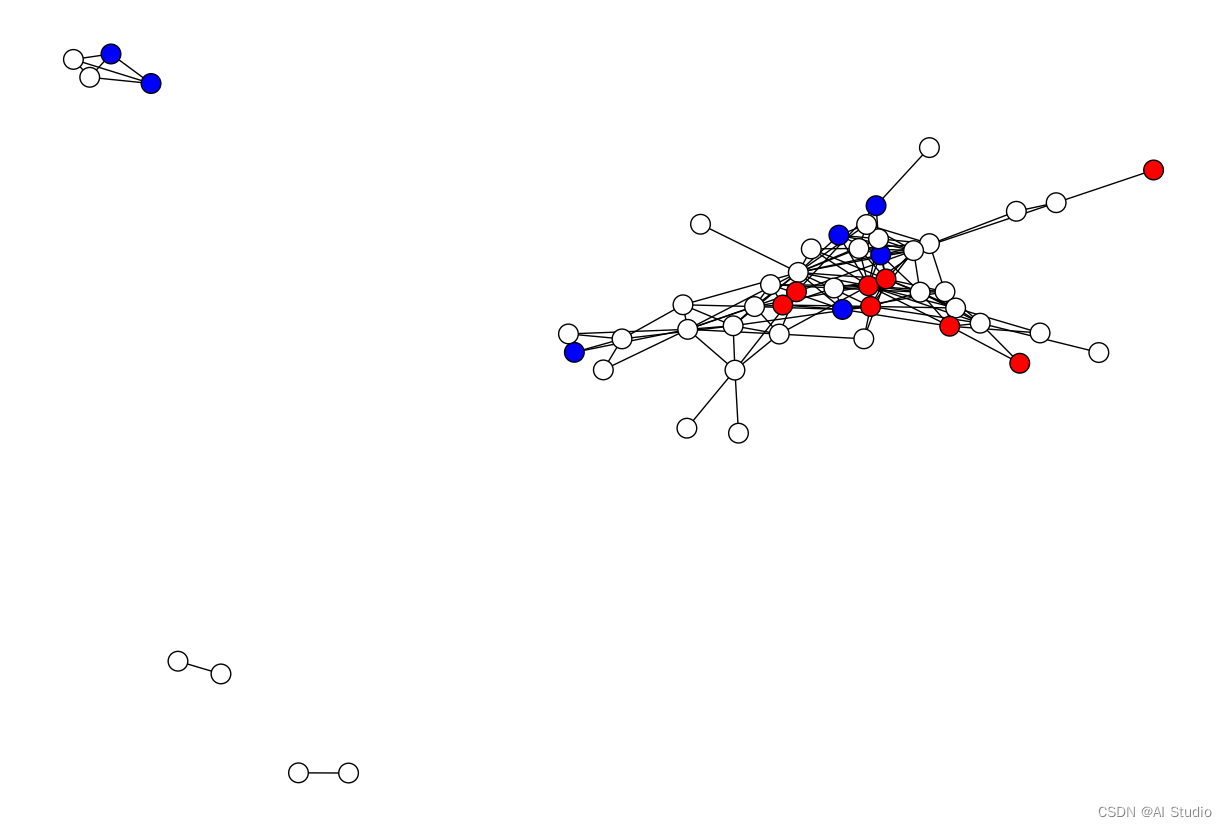
# 为了阐述节点标签预测是如何进行的，我们首先要删掉一些节点的标签，作为要预测的对象。这里我们只保留了30%的节点标签：
random.seed(5)
proportion_nodes = 0.3
labeled_nodes = random.sample(G_fb.nodes(), int(proportion_nodes * G_fb.number_of_nodes()))

known_labels = np.zeros(n)
known_labels[labeled_nodes] = labels[labeled_nodes]

plt.figure(figsize=(12,8))
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = known_labels, node_size=200, pos=pos)
plt.gca().collections[0].set_edgecolor("#000000") # set node border color to black
plt.show()

# 然后，我们就可以进行标签的传播预测：
alpha = 0.7
L_sym = nx.normalized_laplacian_matrix(G_fb)

Y = np.zeros((n,2))
Y[known_labels==-1, 0] = 1
Y[known_labels==1, 1] = 1
I = np.identity(n)

# Create the F-pred matrix
F_pred = np.linalg.inv(I*(1-alpha) + L_sym) * Y
# Identify the prediction as the argmax
pred = np.array(np.argmax(F_pred, axis=1)*2-1).flatten()
# Compute the accuracy score
succ_rate = accuracy_score(labels, pred)

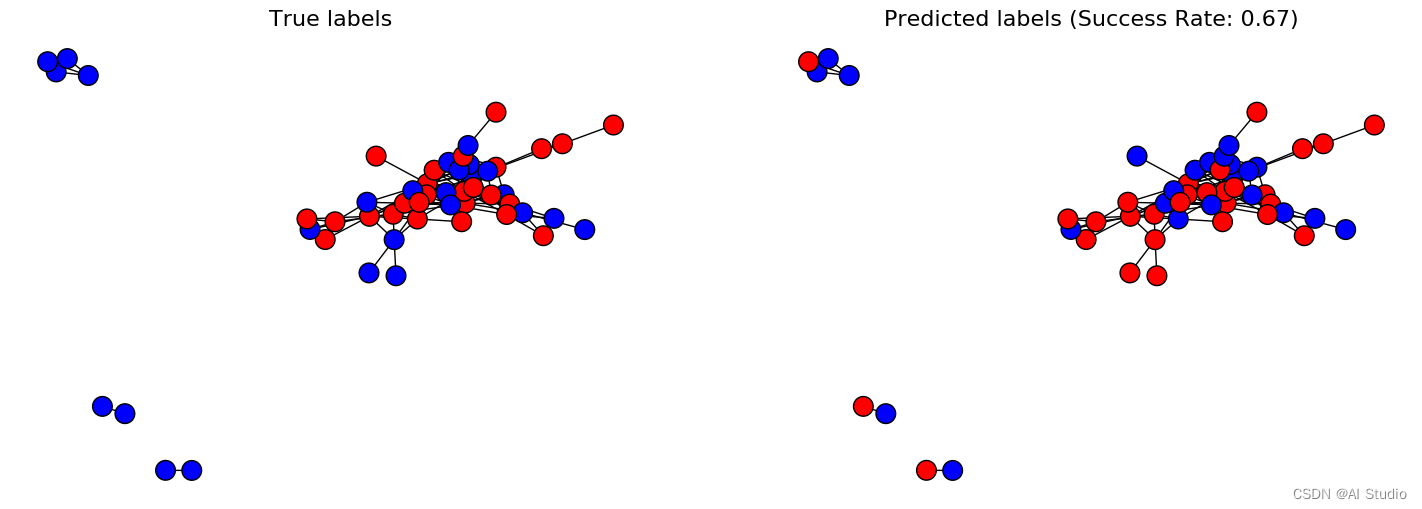
# 我们把结果打印出来
plt.figure(figsize=(18, 6))
f, axarr = plt.subplots(1, 2, num=1)

# Plot true values
plt.sca(axarr[0])
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = labels, node_size=200, pos=pos)
axarr[0].set_title('True labels', size=16)
plt.gca().collections[0].set_edgecolor("#000000")

# Plot predicted values
plt.sca(axarr[1])
nx.draw(G_fb, cmap = plt.get_cmap('bwr'), nodelist=range(n), node_color = pred, node_size=200, pos=pos)
axarr[1].set_title('Predicted labels (Success Rate: %.2f)' % succ_rate, size=16)
plt.gca().collections[0].set_edgecolor("#000000")

1.3 图嵌入（Graph Embedding）

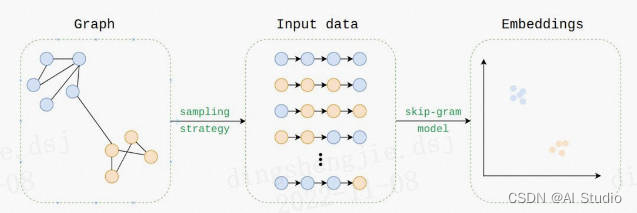
嵌入的学习方式与 word2vec 的 skip-gram 嵌入的学习方式相同，使用的是 skip-gram 模型。问题是，我们如何为 Node2Vec 生成输入语料库？数据要复杂得多，即（非）定向、（非）加权、（a）循环……

为了生成语料库，我们使用随机游走采样策略：

在处理NLP或计算机视觉问题时，我们习惯在深度神经网络中对图像或文本进行嵌入(embedding)。到目前为止，我们所看到的图的一个局限性是没有向量特征。但是，我们可以学习图的嵌入！图有不同几个级别的嵌入：

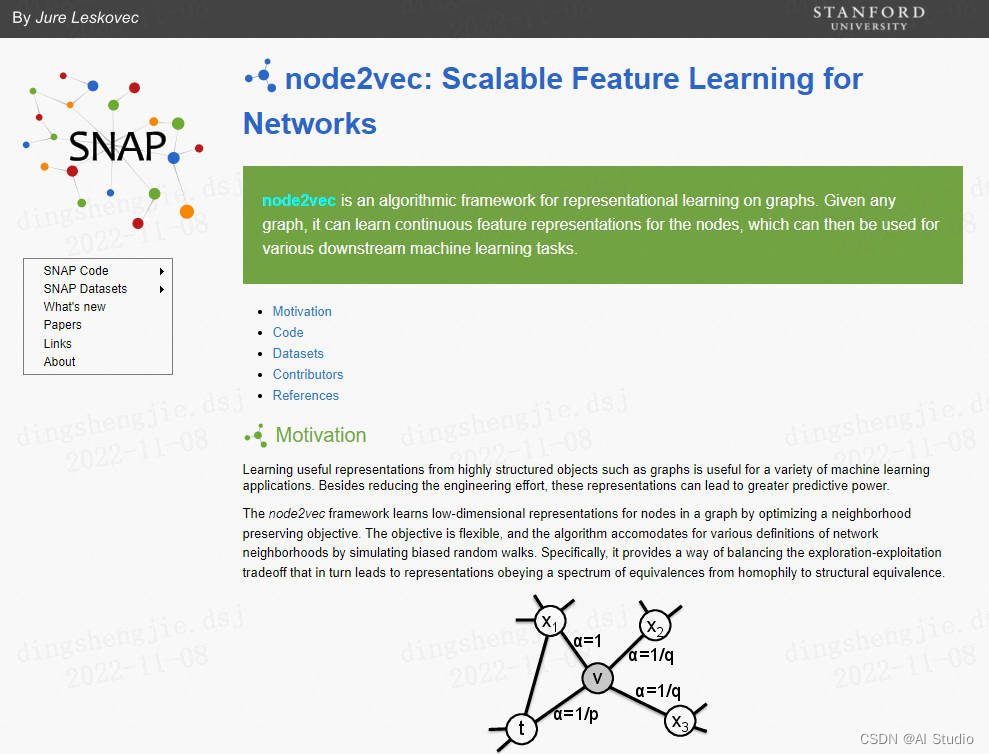
对图的组件进行嵌入（节点，边，特征…）(Node2Vec) node2vec是一个用于图表示学习的算法框架。给定任何图，它可以学习节点的连续特征表示，然后可以用于各种下游机器学习任务。

对图的子图或整个图进行嵌入(Graph2Vec) Learning Distributed Representations of Graphs

学习图的分布式表示

最近关于图结构化数据的表示学习的工作主要集中在学习图子结构（例如节点和子图）的分布式表示。然而，许多图分析任务（例如图分类和聚类）需要将整个图表示为固定长度的特征向量。虽然上述方法自然不具备学习这种表示的能力，但图内核仍然是获得它们的最有效方法。然而，这些图内核使用手工制作的特征（例如，最短路径、graphlet 等），因此受到泛化性差等问题的阻碍。为了解决这个限制，在这项工作中，我们提出了一个名为 graph2vec 的神经嵌入框架来学习任意大小图的数据驱动的分布式表示。图2vec’ s 嵌入是以无监督的方式学习的，并且与任务无关。因此，它们可以用于任何下游任务，例如图分类、聚类甚至播种监督表示学习方法。我们在几个基准和大型现实世界数据集上的实验表明，graph2vec 在分类和聚类精度方面比子结构表示学习方法有显着提高，并且可以与最先进的图内核竞争。

1.3.1. 节点嵌入(Node Embedding)

我们首先关注的是图组件的嵌入。有几种方法可以对节点或边进行嵌入。例如，DeepWalk【http://www.perozzi.net/projects/deepwalk/ 】使用短随机游走来学习图中边的表示。我们将讨论Node2Vec，这篇论文由2016年斯坦福大学的Aditya Grover和Jure Leskovec发表。

作者说：“node2vec是一个用于图表示学习的算法框架。给定任何图，它可以学习节点的连续特征表示，然后可以用于各种下游机器学习任务。“

该模型通过使用随机游走，优化邻域保持目标来学习节点的低维表示。

Node2Vec的代码可以在GitHub上找到：
https://github.com/eliorc/node2vec

import numpy as np
import random
import networkx as nx
from IPython.display import Image
import matplotlib.pyplot as plt

n=34
m = 78
G_karate = nx.karate_club_graph()

pos = nx.spring_layout(G_karate)
nx.draw(G_karate, cmap = plt.get_cmap('rainbow'), with_labels=True, pos=pos)

!pip install node2vec

from node2vec import Node2Vec
# 预先计算概率并生成walks：
node2vec = Node2Vec(G_karate, dimensions=64, walk_length=30, num_walks=200, workers=4)
# 可以对节点进行嵌入
model = node2vec.fit(window=10, min_count=1, batch_words=4)
# 要获取节点的向量，比如节点’2’，使用get_vector：
model.wv.get_vector('2')

HBox(children=(IntProgress(value=0, description='Computing transition probabilities', max=34, style=ProgressSt…





Generating walks (CPU: 4): 100%|██████████| 50/50 [00:04<00:00, 19.45it/s]




array([-0.00948136, -0.05955165,  0.24312176,  0.22371303,  0.00506073,
       -0.20372298, -0.03773373,  0.13210128, -0.1710858 , -0.08046425,
        0.05512173,  0.03490636,  0.14059706, -0.01250026,  0.01621346,
       -0.16618037, -0.10894445,  0.16704279,  0.07081509, -0.09261136,
        0.13090403,  0.03880171,  0.19499338, -0.08031619,  0.12859929,
        0.20997119, -0.20399438,  0.12776034, -0.11047117, -0.05109345,
       -0.08286514,  0.03350278,  0.06221911, -0.12014408,  0.19358768,
       -0.02631716, -0.09489896,  0.17305164,  0.20167911, -0.19484286,
       -0.01220614,  0.09509567, -0.1573437 , -0.16525596, -0.01928455,
       -0.0830077 ,  0.00246636,  0.0563837 , -0.05694559,  0.12744996,
        0.14429945,  0.0378252 ,  0.0070557 ,  0.19148913,  0.23046663,
       -0.10380831, -0.05502449, -0.19360763, -0.03103455, -0.02162319,
       -0.03946753, -0.218418  , -0.16192496, -0.15513903], dtype=float32)

它的长度为64，因为我们在上面将维度定义为64。使用嵌入我们能做些什么？首先想到的就是识别最相似的节点！

model.wv.most_similar('2')
# 它返回最相似节点的列表和相应的概率。
# 如果节点有标签，我们可以训练基于嵌入的算法并附加标签（节点标签，最相似的节点…）

[('13', 0.6633930206298828),
 ('33', 0.6478145122528076),
 ('7', 0.6384901404380798),
 ('30', 0.5996176600456238),
 ('27', 0.5953484773635864),
 ('9', 0.5942345857620239),
 ('3', 0.5686306953430176),
 ('28', 0.5442364811897278),
 ('8', 0.5382028222084045),
 ('31', 0.5166233777999878)]

1.3.2. 边嵌入(Edge Embedding)

边也可以进行嵌入，嵌入可以进一步用于分类。

from node2vec.edges import HadamardEmbedder
edges_embs = HadamardEmbedder(keyed_vectors=model.wv)
# 通过指定2个链接节点的名称来检索向量：
edges_embs[('1','2')]

array([ 3.18152343e-05,  8.73048976e-03,  1.96825750e-02,  1.10771032e-02,
        8.34245002e-05,  5.14624640e-02, -4.61615762e-03,  2.23232470e-02,
        4.34712805e-02, -7.91485596e-04,  9.55235399e-03, -7.25758218e-05,
        2.09876392e-02, -9.48101631e-04, -8.47736432e-04,  2.08098516e-02,
        8.80128983e-03,  2.72566471e-02,  1.03087467e-03, -3.68987955e-03,
        3.24936099e-02,  7.60207139e-03,  3.97971384e-02,  6.72794925e-03,
        1.17940241e-02,  1.33367255e-02,  4.60785180e-02,  8.21675174e-03,
       -5.14448329e-04,  5.64766489e-03,  3.30362329e-03, -2.15062615e-03,
       -7.91513734e-03,  2.56525781e-02,  3.34764901e-03, -5.35957562e-03,
        4.14419826e-03,  1.16991000e-02,  6.50755540e-02, -2.46829875e-02,
       -3.49287386e-03, -6.74469164e-03,  7.06875976e-03,  1.33153042e-02,
        3.29637807e-03, -6.70708995e-03, -1.43668076e-04, -1.30199706e-02,
       -3.71254981e-03, -2.28244043e-03,  2.71325069e-03,  8.63847788e-03,
        7.94410706e-04,  1.56196309e-02,  5.34169935e-02, -5.05916402e-03,
        5.13287261e-04,  4.94767278e-02, -2.78313644e-03,  1.53949019e-03,
       -1.15279406e-02,  2.90202182e-02,  3.90044190e-02, -3.66249047e-02],
      dtype=float32)

# 可以检索最相似的边，可用于缺失边预测，例如：
edges_kv = edges_embs.as_keyed_vectors()
edges_kv.most_similar(str(('1','2')))

Generating edge features: 100%|██████████| 595/595.0 [00:00<00:00, 161706.14it/s]





[("('2', '21')", 0.8356432914733887),
 ("('17', '2')", 0.8148824572563171),
 ("('1', '33')", 0.8079527020454407),
 ("('19', '2')", 0.8064327836036682),
 ("('1', '30')", 0.79854816198349),
 ("('2', '7')", 0.7809598445892334),
 ("('13', '2')", 0.7771724462509155),
 ("('2', '3')", 0.7431320548057556),
 ("('1', '3')", 0.7423675656318665),
 ("('30', '7')", 0.7290617227554321)]

1.3.3 图嵌入(Graph Embedding)

还有一些方法可以直接对图或子图进行嵌入。这种方法已经在Graph2Vec论文中被提出，并且可用于将图或子图表示为向量，从而可以对图进行分类或相似性度量。我不会深入研究这种技术，但请随时查看这个项目的Github：
https://github.com/benedekrozemberczki/graph2vec

它基于与 doc2vec skip-gram 网络相同的想法。

2.图神经网络GNN

2.1GNN引言

图神经网络（Graph Neural Networks，GNN）综述链接：https://zhuanlan.zhihu.com/p/75307407?from_voters_page=true 译文

https://arxiv.org/pdf/1901.00596.pdf 原始文章最新版本V4版本

近年来，深度学习彻底改变了许多机器学习任务，从图像分类和视频处理到语音识别和自然语言理解。这些任务中的数据通常在欧几里得空间中表示。然而，越来越多的应用程序将数据从非欧几里德域生成并表示为具有复杂关系和对象之间相互依赖关系的图。图数据的复杂性对现有的机器学习算法提出了重大挑战。最近，出现了许多关于扩展图数据深度学习方法的研究。在本次调查中，我们全面概述了数据挖掘和机器学习领域中的图神经网络 (GNN)。我们提出了一种新的分类法，将最先进的图神经网络分为四类，即循环图神经网络、卷积图神经网络、图自动编码器和时空图神经网络。我们进一步讨论了图神经网络在各个领域的应用，并总结了图神经网络的开源代码、基准数据集和模型评估。最后，我们在这个快速发展的领域提出了潜在的研究方向

神经网络最近的成功推动了模式识别和数据挖掘的研究。许多机器学习任务，如对象检测 [1]、[2]、机器翻译 [3]、[4] 和语音识别 [5]，曾经严重依赖手工特征工程来提取信息特征集，最近已经由各种端到端深度学习范例彻底改变，例如卷积神经网络 (CNN) [6]、递归神经网络 (RNN) [7] 和自动编码器 [8]。深度学习在许多领域的成功部分归功于快速发展的计算资源（例如 GPU）、大训练数据的可用性以及深度学习从欧几里得数据（例如图像、文本、和视频）。以图像数据为例，我们可以将图像表示为欧几里得空间中的规则网格。卷积神经网络 (CNN) 能够利用图像数据的移位不变性、局部连通性和组合性 [9]。因此，CNN 可以提取与整个数据集共享的局部有意义的特征，用于各种图像分析。

虽然深度学习有效地捕获了欧几里得数据的隐藏模式，但越来越多的应用程序将数据以图形的形式表示。例如，在电子商务中，基于图的学习系统可以利用用户和产品之间的交互来做出高度准确的推荐。在化学中，分子被建模为图形，并且需要确定它们的生物活性以进行药物发现。在引文网络中，论文通过引文相互链接，并且需要将它们分类到不同的组中。图数据的复杂性对现有的机器学习算法提出了重大挑战。由于图可能是不规则的，图可能具有可变大小的无序节点，并且来自图中的节点可能具有不同数量的邻居，导致一些重要的操作（例如卷积）在图像域中很容易计算，但是难以应用于图域。此外，现有机器学习算法的一个核心假设是实例相互独立。这个假设不再适用于图数据，因为每个实例（节点）通过各种类型的链接（例如引用、友谊和交互）与其他实例相关联。

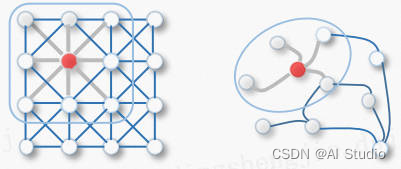
最近，人们对扩展图形数据的深度学习方法越来越感兴趣。受来自深度学习的 CNN、RNN 和自动编码器的推动，在过去几年中，重要操作的新泛化和定义迅速发展，以处理图数据的复杂性。例如，可以从 2D 卷积推广图卷积。如图 1 所示，可以将图像视为图形的特殊情况，其中像素由相邻像素连接。与 2D 卷积类似，可以通过取节点邻域信息的加权平均值来执行图卷积。

二维卷积类似于图，图像中的每个像素都被视为一个节点，其中邻居由过滤器大小确定。 2D 卷积取红色节点及其邻居像素值的加权平均值。节点的邻居是有序的并且具有固定的大小。

图卷积。为了得到红色节点的隐藏表示，图卷积运算的一个简单解决方案是取红色节点及其邻居节点特征的平均值。与图像数据不同，节点的邻居是无序且大小可变的。

发展：

图神经网络 (GNN) Sperduti 等人的简史。 (1997) [13] 首次将神经网络应用于有向无环图，这激发了对 GNN 的早期研究。图神经网络的概念最初是在 Gori 等人中概述的。 (2005) [14] 并在 Scarselli 等人中进一步阐述。 (2009) [15] 和 Gallicchio 等人。 (2010) [16]。这些早期研究属于循环图神经网络（RecGNNs）的范畴。他们通过以迭代方式传播邻居信息来学习目标节点的表示，直到达到一个稳定的固定点。这个过程在计算上是昂贵的，并且最近已经越来越多地努力克服这些挑战[17]，[18]。
受 CNN 在计算机视觉领域的成功的鼓舞，大量重新定义图数据卷积概念的方法被并行开发。这些方法属于卷积图神经网络 (ConvGNN) 的范畴。 ConvGNN 分为两个主流，基于光谱的方法和基于空间的方法。 Bruna 等人提出了第一个关于基于光谱的 ConvGNN 的杰出研究。（2013）[19]，它开发了一种基于谱图理论的图卷积。从那时起，基于谱的 ConvGNN [20]、[21]、[22]、[23] 的改进、扩展和近似值不断增加。基于空间的 ConvGNN 的研究比基于光谱的 ConvGNN 早得多。 2009 年，Micheli 等人。 [24] 首先通过架构复合非递归层解决了图相互依赖问题，同时继承了 RecGNN 的消息传递思想。然而，这项工作的重要性被忽视了。直到最近，出现了许多基于空间的 ConvGNN（例如，[25]、[26]、[27]）。代表性 RecGNNs 和 ConvGNNs 的时间线如表 II 的第一列所示。除了 RecGNNs 和 ConvGNNs，在过去几年中还开发了许多替代 GNN，包括图自动编码器 (GAE) 和时空图神经网络 (STGNN)。这些学习框架可以建立在 RecGNN、ConvGNN 或其他用于图建模的神经架构上。

综述总结如下：

新分类我们提出了一种新的图神经网络分类。图神经网络分为四组：循环图神经网络、卷积图神经网络、图自动编码器和时空图神经网络。
综合回顾我们提供了最全面的图数据现代深度学习技术概览。对于每种类型的图神经网络，我们都提供了代表性模型的详细描述，进行了必要的比较，并总结了相应的算法。
丰富的资源我们收集了丰富的图神经网络资源，包括最先进的模型、基准数据集、开源代码和实际应用。本调查可用作理解、使用和开发适用于各种现实生活应用的不同深度学习方法的实践指南。
未来方向我们讨论了图神经网络的理论方面，分析了现有方法的局限性，并在模型深度、可扩展性权衡、异质性和动态性方面提出了四个可能的未来研究方向。

2.2 神经网络类型

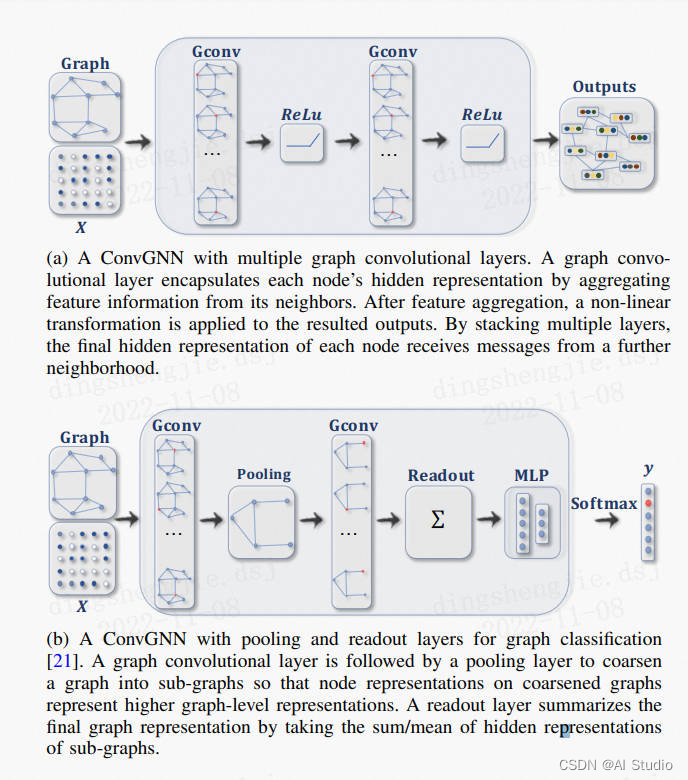
在本节中，我们介绍了图神经网络 (GNN) 的分类，如表 II 所示。我们将图神经网络 (GNN) 分为循环图神经网络 (RecGNN)、卷积图神经网络 (ConvGNN)、图自动编码器 (GAE) 和时空图神经网络 (STGNN)。图 2 给出了各种模型架构的示例。下面，我们对每个类别进行简要介绍。

2.2.1循环图神经网络（RecGNNs，Recurrent graph neural networks ）

循环图神经网络（RecGNNs）大多是图神经网络的先驱作品。 RecGNN 旨在学习具有循环神经架构的节点表示。他们假设图中的一个节点不断地与其邻居交换信息/消息，直到达到稳定的平衡。 RecGNN 在概念上很重要，并启发了后来对卷积图神经网络的研究。特别是，基于空间的卷积图神经网络继承了消息传递的思想。

2.2.2 卷积图神经网络 (ConvGNNs，Convolutional graph neural networks)

卷积图神经网络 (ConvGNNs) 将卷积操作从网格数据推广到图数据。主要思想是通过聚合它自己的特征 xv 和邻居的特征 xu 来生成节点 v 的表示，其中 u ∈ N(v)。与 RecGNN 不同，ConvGNN 堆叠多个图卷积层以提取高级节点表示。 ConvGNN 在构建许多其他复杂的 GNN 模型中发挥着核心作用。图 2a 显示了用于节点分类的 ConvGNN。图 2b 展示了用于图分类的 ConvGNN。

2.2.3图自动编码器 (GAE，Graph autoencoders (GAEs))

是无监督学习框架，它将节点/图编码到潜在向量空间并从编码信息中重建图数据。 GAE 用于学习网络嵌入和图形生成分布。对于网络嵌入，GAE 通过重构图结构信息（例如图邻接矩阵）来学习潜在节点表示。对于图的生成，一些方法逐步生成图的节点和边，而另一些方法一次全部输出图。图 2c 展示了一个用于网络嵌入的 GAE。

2.2.4 时空图神经网络 (STGNN，Spatial-temporal graph neural networks)

旨在从时空图中学习隐藏模式，这在各种应用中变得越来越重要，例如交通速度预测 [72]、驾驶员机动预期 [73] 和人类动作识别 [ 75]。 STGNN 的关键思想是同时考虑空间依赖和时间依赖。许多当前的方法集成了图卷积来捕获空间依赖性，并使用 RNN 或 CNN 对时间依赖性进行建模。图 2d 说明了用于时空图预测的 STGNN。

具体公式推到见论文！

2.3图神经网络的应用

GNN 在不同的任务和领域中有许多应用。尽管每个类别的 GNN 都可以直接处理一般任务，包括节点分类、图分类、网络嵌入、图生成和时空图预测，但其他与图相关的一般任务，如节点聚类 [134]、链接预测 [135 ]，图分割[136]也可以通过GNN来解决。我们详细介绍了基于以下研究领域的一些应用。

计算机视觉（Computer vision）

计算机视觉 GNN 在计算机视觉中的应用包括场景图生成、点云分类和动作识别。识别对象之间的语义关系有助于理解视觉场景背后的含义。

场景图生成模型旨在将图像解析为由对象及其语义关系组成的语义图 [137]、[138]、[139]。另一个应用程序通过在给定场景图的情况下生成逼真的图像来反转该过程 [140]。由于自然语言可以被解析为每个单词代表一个对象的语义图，因此它是一种很有前途的解决方案，可以在给定文本描述的情况下合成图像。

分类和分割点云使 LiDAR 设备能够“看到”周围环境。点云是由 LiDAR 扫描记录的一组 3D 点。 [141]、[142]、[143] 将点云转换为 k-最近邻图或超点图，并使用 ConvGNN 探索拓扑结构。

识别视频中包含的人类行为有助于从机器方面更好地理解视频内容。一些解决方案检测视频剪辑中人体关节的位置。由骨骼连接起来的人体关节自然形成了一个图形。给定人类关节位置的时间序列，[73]、[75] 应用 STGNN 来学习人类动作模式。

此外，GNN 在计算机视觉中的适用方向数量仍在增长。它包括人-物交互[144]、小样本图像分类[145]、[146]、[147]、语义分割[148]、[149]、视觉推理[150]和问答[151]。

自然语言处理（Natural language processing ）

自然语言处理 GNN 在自然语言处理中的一个常见应用是文本分类。 GNN 利用文档或单词的相互关系来推断文档标签 [22]、[42]、[43]。

尽管自然语言数据表现出顺序，但它们也可能包含内部图结构，例如句法依赖树。句法依赖树定义了句子中单词之间的句法关系。 Marcheggiani 等人。 [152] 提出了在 CNN/RNN 句子编码器之上运行的句法 GCN。 Syntactic GCN 基于句子的句法依赖树聚合隐藏的单词表示。巴斯廷斯等人。 [153] 将句法 GCN 应用于神经机器翻译任务。 Marcheggiani 等人。[154] 进一步采用与 Bastings 等人相同的模型。
[153]处理句子的语义依赖图。

图到序列学习学习在给定抽象词的语义图（称为抽象意义表示）的情况下生成具有相同含义的句子。宋等人。 [155] 提出了一种图 LSTM 来编码图级语义信息。贝克等人。 [156] 将 GGNN [17] 应用于图到序列学习和神经机器翻译。逆向任务是序列到图的学习。给定句子生成语义或知识图在知识发现中非常有用

交通 Traffic

 准确预测交通网络中的交通速度、交通量或道路密度对于智能交通系统至关重要。 [48]、[72]、[74] 使用 STGNN 解决交通预测问题。 他们将交通网络视为一个时空图，其中节点是安装在道路上的传感器，边缘由节点对之间的距离测量，每个节点将窗口内的平均交通速度作为动态输入特征。 另一个工业级应用是出租车需求预测。 鉴于历史出租车需求、位置信息、天气数据和事件特征，Yao 等人。 [159] 结合 LSTM、CNN 和由 LINE [160] 训练的网络嵌入，形成每个位置的联合表示，以预测时间间隔内某个位置所需的出租车数量。

化学 Chemistry

在化学领域，研究人员应用 GNN 来研究分子/化合物的图形结构。 在分子/化合物图中，原子被视为节点，化学键被视为边缘。 节点分类、图分类和图生成是针对分子/化合物图的三个主要任务，以学习分子指纹 [85]、[86]、预测分子特性 [27]、推断蛋白质界面 [164] 和 合成化合物

其他

GNN 的应用不仅限于上述领域和任务。 已经探索将 GNN 应用于各种问题，例如程序验证 [17]、程序推理 [166]、社会影响预测 [167]、对抗性攻击预防 [168]、电子健康记录建模 [169]、[170] ]、大脑网络[171]、事件检测[172]和组合优化[173]。

2.4未来方向

尽管 GNN 已经证明了它们在学习图数据方面的能力，但由于图的复杂性，挑战仍然存在。

模型深度 Model depth

深度学习的成功在于深度神经架构 [174]。然而，李等人。表明随着图卷积层数的增加，ConvGNN 的性能急剧下降 [53]。随着图卷积将相邻节点的表示推得更近，理论上，在无限数量的图卷积层中，所有节点的表示将收敛到一个点 [53]。这就提出了一个问题，即深入研究是否仍然是学习图数据的好策略。

可扩展性权衡 Scalability trade-off

GNN 的可扩展性是以破坏图完整性为代价的。无论是使用采样还是聚类，模型都会丢失部分图信息。通过采样，节点可能会错过其有影响力的邻居。通过聚类，图可能被剥夺了独特的结构模式。如何权衡算法的可扩展性和图的完整性可能是未来的研究方向。

异质性Heterogenity

当前的大多数 GNN 都假设图是同质的。目前的 GNN 很难直接应用于异构图，异构图可能包含不同类型的节点和边，或者不同形式的节点和边输入，例如图像和文本。因此，应该开发新的方法来处理异构图。

动态Dynamicity

图本质上是动态的，节点或边可能出现或消失，节点/边输入可能会随时间变化。需要新的图卷积来适应图的动态性。虽然图的动态性可以通过 STGNN 部分解决，但很少有人考虑在动态空间关系的情况下如何执行图卷积。

总结

因为之前一直在研究知识提取相关算法，后续为了构建小型领域知识图谱，会用到知识融合、知识推理等技术，现在开始学习研究图计算相关。

现在已经覆盖了图的介绍，图的主要类型，不同的图算法，在Python中使用Networkx来实现它们，以及用于节点标记，链接预测和图嵌入的图学习技术，最后讲了GNN应用。

本项目参考了：maelfabien大神、以及自尊心3 在博客 or github上的贡献

欢迎大家fork，后续将开始图计算相关项目以及部分知识提取技术深化！

项目参考链接：

第一章节：

https://maelfabien.github.io/machinelearning/graph_4/#ii-node-labeling

https://blog.csdn.net/xjxgyc/article/details/100175930

https://maelfabien.github.io/machinelearning/graph_5/#node-embedding

https://github.com/eliorc/node2vec

第二节：

https://zhuanlan.zhihu.com/p/75307407?from_voters_page=true 译文

https://arxiv.org/pdf/1901.00596.pdf

更多参考：

https://github.com/maelfabien/Machine_Learning_Tutorials

此文章为搬运
原项目链接

今天的文章图机器学习(GML)&图神经网络(GNN)原理和代码实现(前置学习系列二）分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/83598.html

图机器学习(GML)&图神经网络(GNN)原理和代码实现(前置学习系列二）

图机器学习(GML)&图神经网络(GNN)原理和代码实现（PGL）[前置学习系列二]

1. 图机器学习GML

1.1链接预测（Link prediction）

1.1.1 相似度分数

1.1.2 性能指标(Performance metrics)

1.1.3 代码实践

1.2 节点标记预测（Node labeling）

1.2.1 代码实现标签扩散

1.3 图嵌入（Graph Embedding）

1.3.1. 节点嵌入(Node Embedding)

1.3.2. 边嵌入(Edge Embedding)

1.3.3 图嵌入(Graph Embedding)

2.图神经网络GNN

2.1GNN引言

2.2 神经网络类型

2.2.1循环图神经网络（RecGNNs，Recurrent graph neural networks ）

2.2.2 卷积图神经网络 (ConvGNNs，Convolutional graph neural networks)

2.2.3图自动编码器 (GAE，Graph autoencoders (GAEs))

2.2.4 时空图神经网络 (STGNN，Spatial-temporal graph neural networks)

2.3图神经网络的应用

计算机视觉（Computer vision）

自然语言处理（Natural language processing ）

交通 Traffic

推荐系统 Recommender systems

化学 Chemistry

其他

2.4未来方向

模型深度 Model depth

可扩展性权衡 Scalability trade-off

异质性Heterogenity

动态Dynamicity

总结

发表回复

图机器学习(GML)&图神经网络(GNN)原理和代码实现(前置学习系列二）

图机器学习(GML)&图神经网络(GNN)原理和代码实现（PGL）[前置学习系列二]

1. 图机器学习GML

1.1链接预测（Link prediction）

1.1.1 相似度分数

1.1.2 性能指标(Performance metrics)

1.1.3 代码实践

1.2 节点标记预测（Node labeling）

1.2.1 代码实现标签扩散

1.3 图嵌入（Graph Embedding）

1.3.1. 节点嵌入(Node Embedding)

1.3.2. 边嵌入(Edge Embedding)

1.3.3 图嵌入(Graph Embedding)

2.图神经网络GNN

2.1GNN引言

2.2 神经网络类型

2.2.1循环图神经网络（RecGNNs，Recurrent graph neural networks ）

2.2.2 卷积图神经网络 (ConvGNNs，Convolutional graph neural networks)

2.2.3图自动编码器 (GAE，Graph autoencoders (GAEs))

2.2.4 时空图神经网络 (STGNN，Spatial-temporal graph neural networks)

2.3图神经网络的应用

计算机视觉（Computer vision）

自然语言处理（Natural language processing ）

交通 Traffic

推荐系统 Recommender systems

化学 Chemistry

其他

2.4未来方向

模型深度 Model depth

可扩展性权衡 Scalability trade-off

异质性Heterogenity

动态Dynamicity

总结

相关推荐

发表回复