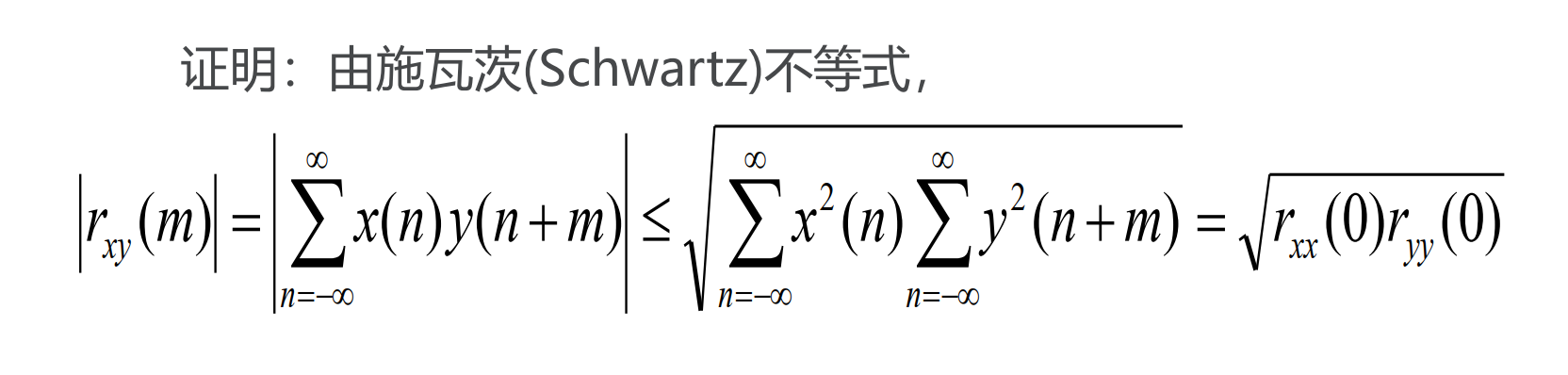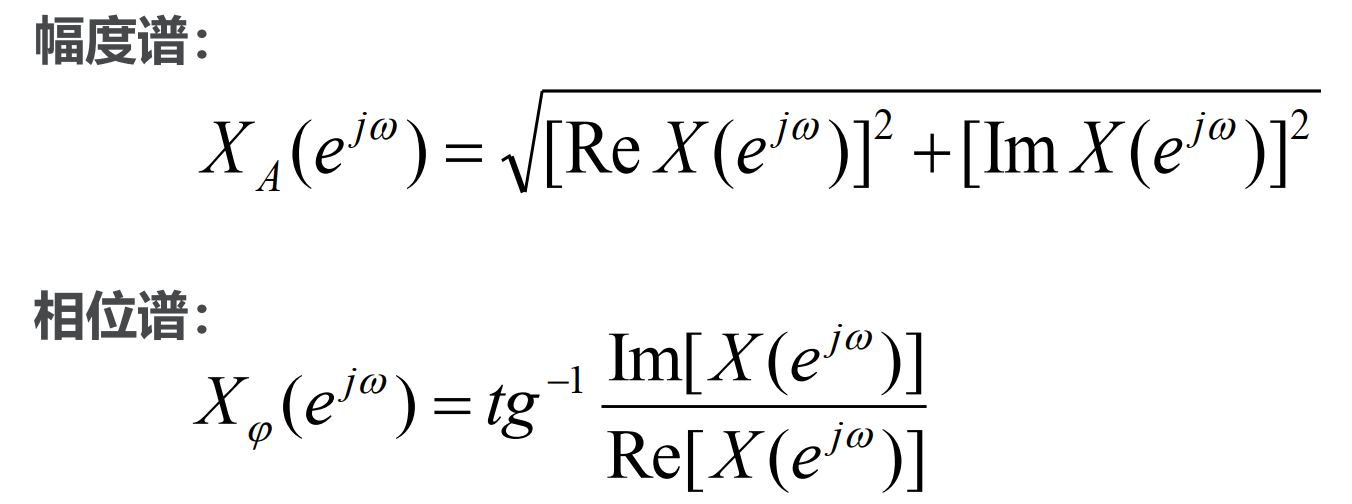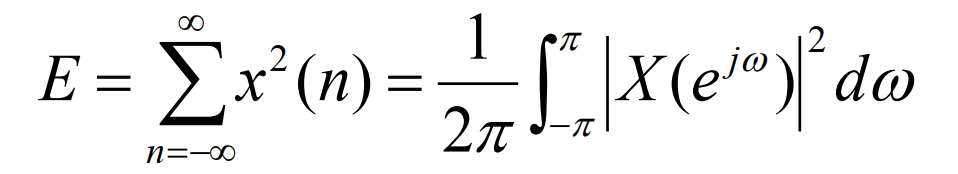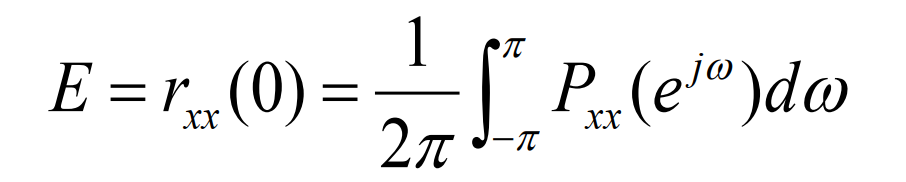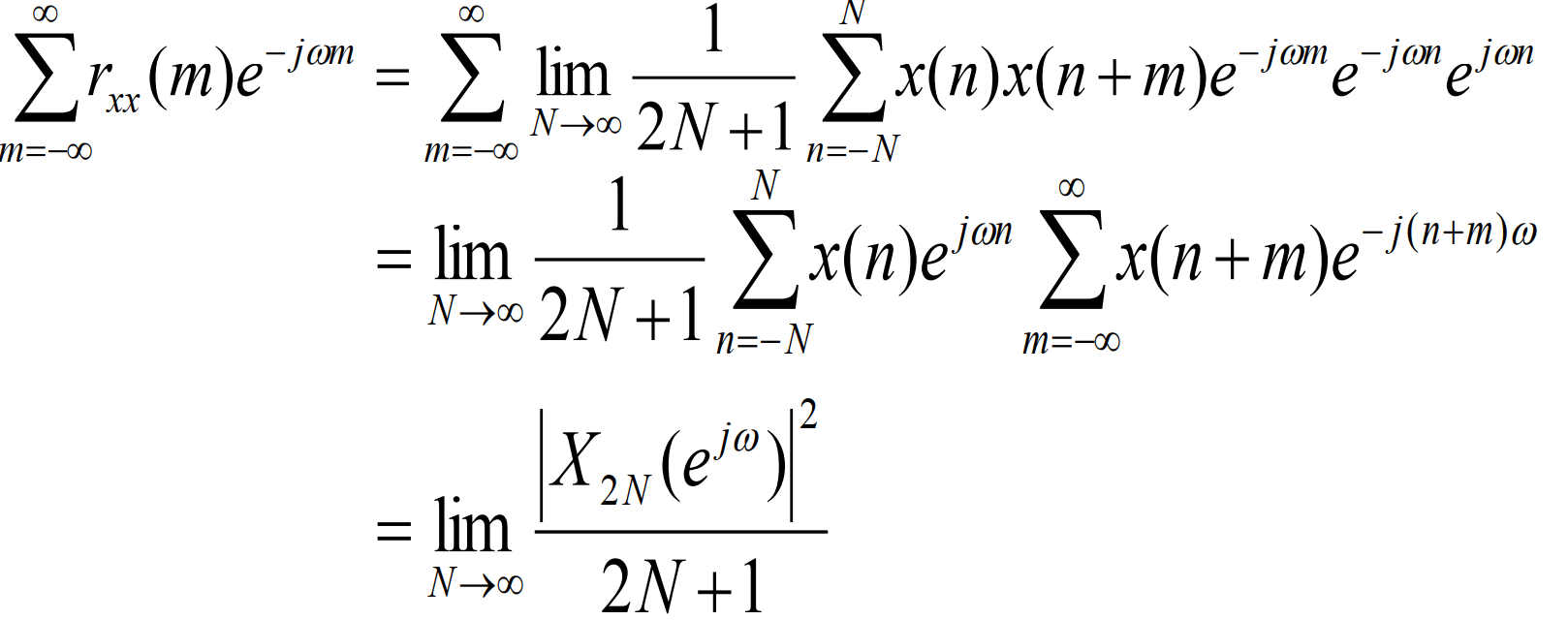互相关卷积_n阶矩

一. 互相关函数

信号y(n)延迟m个时间间隔后与x(n)的互相关函数定义如下：

$r_{xy}(m)=\sum_{n=-\infty}^\infty x(n)y(n+m)$

此定义可以理解为x(n)不动，y(n)左移m个时间单位后与x(n)对应相乘求和的结果。其中平移过程满足左加右减原则，n代表时间，m代表平移量。

调换x和y的位置，也就是y(n)不动，来平移x(n)，可得：

$r_{yx}(m)=\sum_{n=-\infty}^\infty y(n)x(n+m)=\sum_{k=-\infty}^\infty x(k)y(k-m)=r_{xy}(-m)$

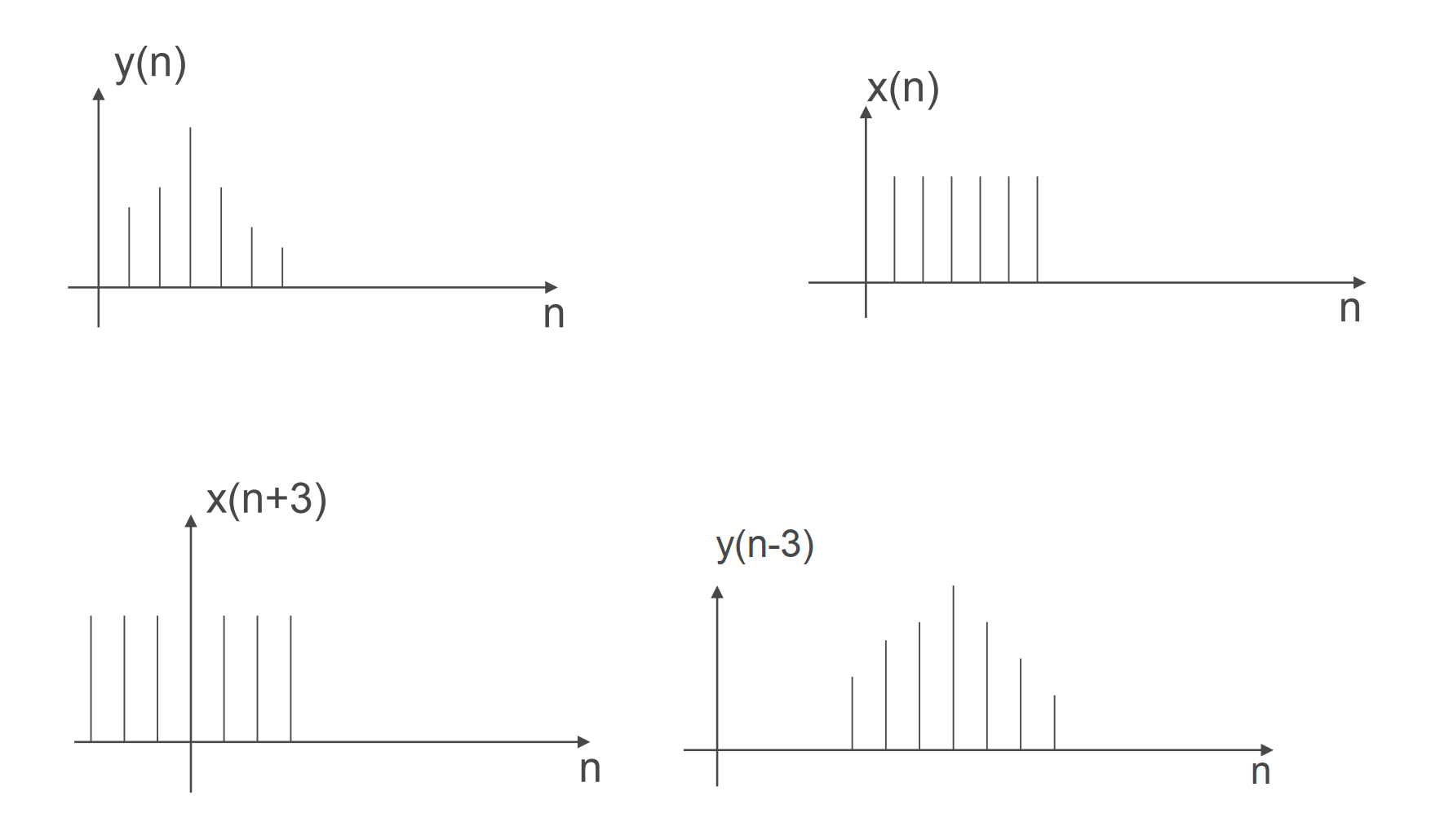
理解其几何意义：

$r_{yx}(m)$ ：y(n)不动，x(n)左移m个延迟单位与y(n)相乘求和的结果；
$r_{xy}(-m)$ ：x(n)不动，y(n)右移m个延迟单位后与x(n)相乘求和，此时与 $r_{yx}(m)$ 的几何意义是等效的；

关于延迟的图像理解如下：

若x(n)和y(n)是复信号，也就是在复数域内的运算，此时需要引入共轭的性质，则相关函数定义如下：

$r_{xy}(m)=\sum_{n=-\infty}^\infty x^*(n)y(n+m)$

上式子中“*”表示取共轭的过程。

如果x(n)与y(n)是功率信号，那么原定义求出的结果趋于无限大（这个很容易证明，本处略），没有物理意义，此时相关函数修改为如下：

$r_{xy}(m)=\lim_{N\to \infty}\frac{1}{2N+1}\sum_{n=-N}^N x(n)y(n+m)$

二. 自相关函数

若y(n)=x(n),则互相关函数变成了自相关函数，如下：

$r_{xx}(m)=\sum_{n=-\infty}^\infty x(n)x(n+m)$

自相关函数反映了x(n)与自身左移m个时间单位后的信号x(n+m)的相似程度。

相关性函数可用来衡量信号的相似程度。

若x(n)是功率信号，自相关函数定义为如下：

$r_{xx}(m)=\lim_{N\to \infty}\frac{1}{2N+1}\sum_{n=-N}^N x(n)x(n+m)$

2.1 自相关函数是一个偶函数

根据定义可得：

$r_{xx}(-m)=\sum_{n=-\infty}^\infty x(n)x[n+(-m)]$

令k=n-m，可得：

$r_{xx}(-m)=\sum_{k=-\infty}^\infty x(k+m)x(k)=r_{xx}(m)$

所以 $r_{xx}(m)$ 是偶函数，即：

$r_{xx}(-m)=r_{xx}(m)$

对于自相关函数来讲，往右平移和往左平移是等效的。

2.2 自相关函数在m=0时，取得最大值

首先易得：

$\sum_{n=-\infty}^\infty [x(n)\pm x(n+m)]^2\geq0$

展开平方项，可得：

$\sum_{n=-\infty}^\infty x^2(n)+\sum_{n=-\infty}^\infty x^2(n+m)\geq \pm2\sum_{n=-\infty}^\infty x(n)x(n+m)$

化简左边形式，可得：

$2\sum_{n=-\infty}^\infty x^2(n)\geq \pm2\sum_{n=-\infty}^\infty x(n)x(n+m)$

所以可得：

$r_{xx}(0)\geq \pm r_{xx}(m)$

最终可得：

$r_{xx}(0)\geq |r_{xx}(m)|$

不平移的话，类似平方的形式，值最大。

2.3 极限性质

若x(n)是能量信号，则有如下极限性质：

$\lim_{|m|\to \infty}r_{xx}(m)=0$

此极限可以理解成，能量有限信号随着时移量逐渐增加，其相关性就逐渐消失，可以从能量有限的角度来理解这个极限。感兴趣的小伙伴可以参考此本书，更加详细：

《信号数字处理的数学原理》程乾生石油工业出版社 1979年

2.4 周期信号的自相关函数也是周期的，且与原信号周期相同

假设x(n)的周期为2N+1，所以可得：

容易证明周期性是保留的

三. 互相关函数的性质

$r_{xy}(m)$ 不是偶函数，但是满足如下关系：

$r_{xy}(m)=r_{yx}(-m)$

3.1 函数上界

$r_{xy}(m)$ 具有一个上界：

$|r_{xy}(m)|\leq \sqrt{r_{xx}(0)r_{yy}(0)}$

3.2 极限相关

若x(n)和y(n)是能量信号，那么有：

$\lim_{|m|\to\infty}r_{xy}(m)=0$

根据定义， $r_{xy}(m)$ 只包含了信号x(n)和y(n)的共有频率成分，所以只有当 $X(e^{j\omega})$ 和 $Y(e^{j\omega})$ 都不为0时， $P(e^{j\omega})$ 才不为0。

四. 谱分析

4.1 频谱

假设x(n)为能量信号，则其傅氏Z变换称为x(n)的频谱，如下：

$X(e^{j\omega})=\sum_{n=-\infty}^\infty x(n)e^{-j\omega n}$

Z 变换是离散时间信号与离散时间系统分析与综合的重要工具，其作用相当于连续时间信号与系统的拉氏变换分析方法。Z 变换的基本思想、许多性质及其分析方法都与拉氏变换有相似之处。

一般而言，上式中计算出的频谱为复函数，包含幅度谱和相位谱，如下：

4.2 能量谱

根据帕塞瓦尔定理，有：

根据自相关函数定义可得：

所以可得：

$P_{xx}(e^{j\omega})=|X(e^{j\omega})|^2$

此反映了信号能量E在频域的分布于，称之为信号的能量密度谱，简称能量谱。

4.3 功率谱

将功率信号x(n)进行截短，形成 $x_{2N}(n)$ ，如下：

N \end{cases}”>

显然 $|X_{2N}(e^{j\omega})|$ 是 $x_{2N}(n)$ 的能量谱，根据功率信号自相关函数，可得：

如果该极限可以求出来的话，根据维纳-辛钦定理，则称如下式子为功率密度谱：

$S(e^{j\omega})=\lim_{N\to\infty}\frac{|X_{2N}(e^{j\omega})|^2}{2N+1}$

功率密度谱也被简称为功率谱。

五. 随机信号的k阶矩

随机信号{x(t)}的k阶矩，定义为：

$\mu(t_1,\cdots,t_k)=E\lbrace x(t_1),\cdots,x(t_k)\rbrace$

由此，一阶矩与均值相关：

$\mu(t)=E\lbrace x(t)\rbrace=\int_{-\infty}^\infty xf(x,t)dx$

二阶矩与自相关函数相关：

$R_x(t_1,t_2)=E\lbrace x(t_1)x^*(t_2)\rbrace$

根据k阶矩是否与时间有关，可以把随机信号分成平稳随机信号和非平稳随机信号。

六. MATLAB代码（卷积计算）

在 MATLAB 中，提供了卷积函数 conv，即 y=conv(x,h)，调用十分方便，我们来看一个例子：

clear;
clc;
close all; %清空参数

n=1:50; %定义序列的长度是50，间隔为1，画出的图像为一个个点
hb=zeros(1,50); %注意：MATLAB 中数组下标从 1 开始
hb(1)=1; hb(2)=2.5; hb(3)=2.5; hb(4)=1;
close all; 
subplot(3,1,1); %图像3行1列，第一个图像
stem(hb);
title('系统 hb[n]');
m=1:50; 
T=0.001; %定义序列的长度是和采样率
A=444.128; a=50*sqrt(2.0)*pi; %设置信号有关的参数
w0=50*sqrt(2.0)*pi;
x=A*exp(-a*m*T).*sin(w0*m*T); %pi 是 MATLAB 定义的π，信号乘可采用“.*”
subplot(3,1,2);
stem(x);
title('输入信号 x[n]');
y=conv(x,hb);
subplot(3,1,3);
stem(y);
title('输出信号 y[n]');

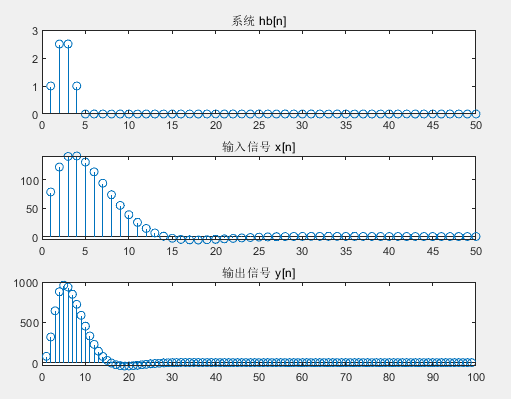
运行结果：

今天的文章互相关卷积_n阶矩分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/83649.html

互相关 卷积_n阶矩