句法结构乔姆斯基pdf_乔姆斯基的普遍语法理论

在上一部分中，我们介绍了NLP领域最基本的问题：词法分析，现阶段解决该问题最常用的方法就是将其转化为序列标注问题，根据解决序列标注问题的方法对其进行解决。
词的问题解决了，那么下一步，就是句法分析。
在这一部分中，我们介绍完全句法分析的基础——Chomsky形式文法。

句法分析的任务是确定句子的句法结构或句子中词汇之间的依存关系，主要包括三种：完全句法分析、局部句法分析、依存关系分析。
其中，前两种句法分析是对句子的句法结构进行分析（也称为短语结构分析），而后一种是对句子中词汇间的依存关系进行分析，我们在后文中将有所介绍。

1.完全句法分析

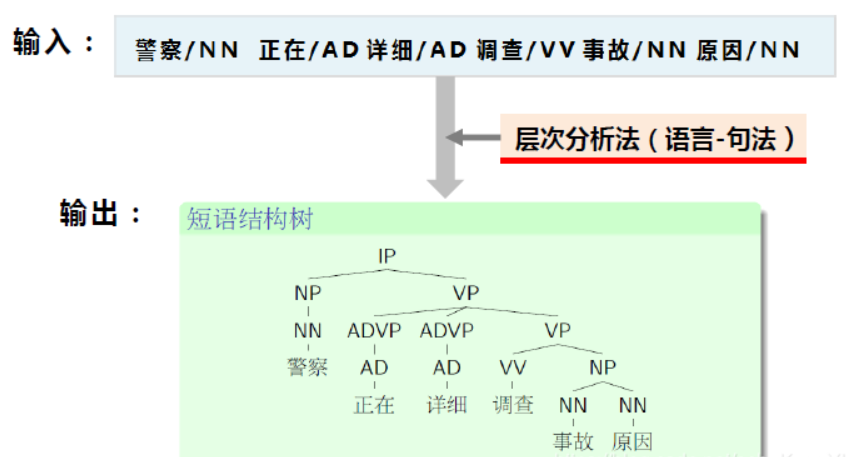
在完全句法分析任务中，我们手中已经得到了曾进行过词法分析的句子，目的是得到句子的句法结构，通常用短语结构树来表示。
对词法分析不熟悉的朋友们可以参看博客：NLP入门概览（6） ——词法分析
也就是说，完全句法分析的任务可以描述如下：

解决该任务的方法依然是我们曾经提到过的三种方法：规则法、概率统计法、深度学习法（多数NLP问题的解决方法都是这三种）。

那么，在上图中，我们通过一个叫做“层次分析法”的方法将已经进行过词法分析的句子处理为一棵短语结构树。

2.层次分析法

那么，什么是层次分析法呢？
层次分析法就是利用语言学，从句子结构层面对句子进行分析：

将句子分为主语、谓语、宾语、定语、状语、补语六个成分；
以词或词组作为划分成分的基本单位；
根据六个成分的搭配排列按层次顺序确定句子的格局。

一般来说，以树结构表示结果，我们将其称为句法分析树（也就是上文提到的短语结构树）。
分析的时候，往往找出主语和谓语作为句子的主干，以其他成分作为枝叶，描述整个句子的结构。

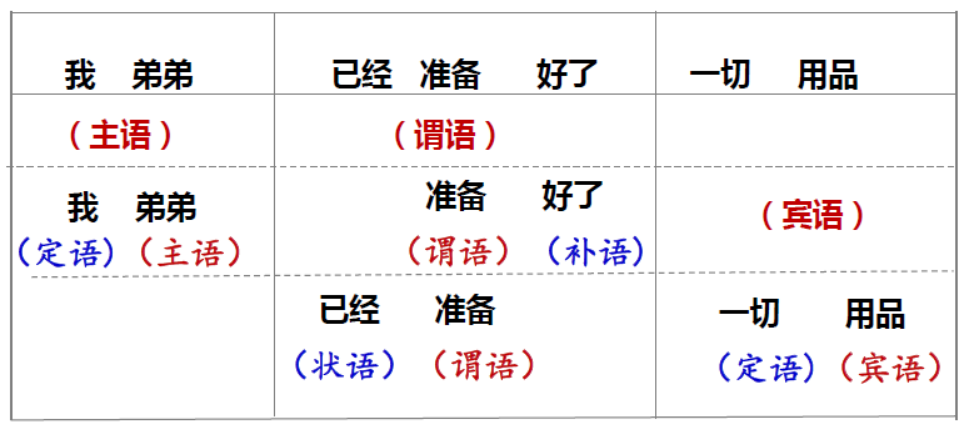
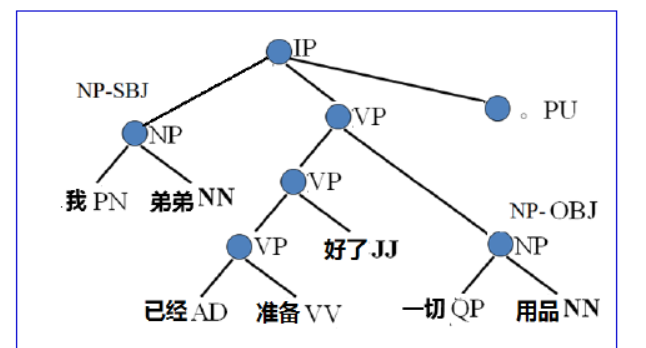
举个例子：“我弟弟已经准备好了一切用品。”

由此我们可以得到一棵句法分析树：

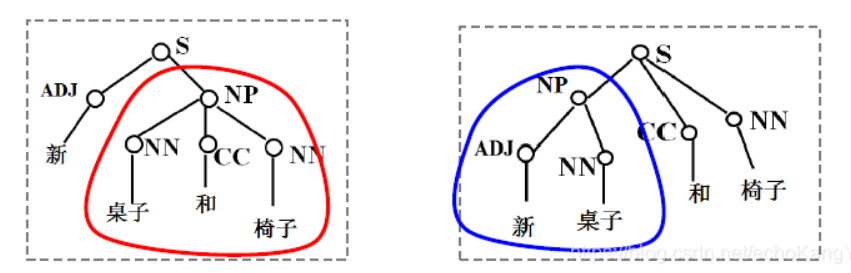
由此可见，层次分析法枝干分明，便于归纳句型。然而，这种方法会遇到大量的歧义，比如对于“新桌子和椅子”，它会产生如下歧义：

此外，层次分析法还面临着很多困难：
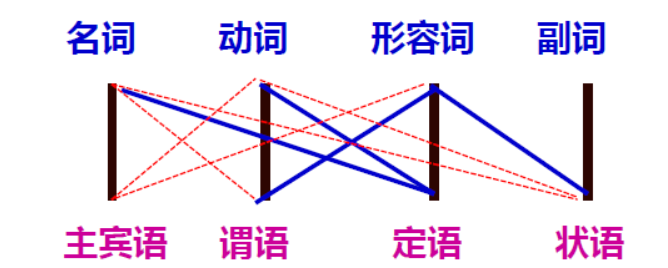
1.在汉语中，词类跟句法成分之间的关系比较复杂，除了副词只能作状语（一对一）之外，其余的都是一对多，即一种词类可以作多种句法成分：

图中黑线表示词类的主要功能，蓝线表示次要功能，红线表示局部功能。
2.词存在兼类
例如：“每次他都会在会上制造新闻。”
其中第一个“会”是名词，表示会议；而第二个“会”是动词，表示能够。
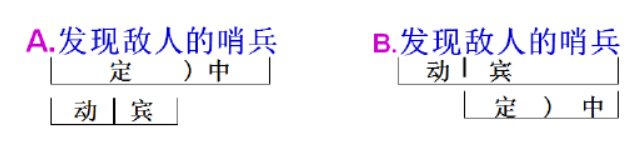
3.短语存在多义
例如：

3.Chomsky形式文法

在完全句法分析中，Chomsky形式文法是极为重要的理论。

Chomsky形式语言自诞生之日起至今，历经古典理论、标准理论、扩充式标准理论、管辖约束理论和最简理论五个阶段的发展变化。它在语言学界产生了重大影响，被誉为一场Chomsky式的革命。其影响力波及到语言学之外的心理学、哲学、教育学、逻辑学、翻译理论、通讯技术、计算机科学等领域。

3.1 Chomsky文法

Chomsky文法用 G GG 表示形式语法，将其表示为四元组：
$G = (V_n,V_t,S,P)$
其中各变量定义如下：
$V_n$ :非终结符的有限集合，不能处于生成过程的终点，即在实际句子中不出现。在推导中起变量作用，相当于语言中的语法范畴；
$V_t$ ：终结符的有限集合，只处于生成过程的终点，是句子中实际出现的符号，相当于单词表。
$S$ ： $V_n$ 中的初始符号，相当于语法范畴中的句子。
$P$ ：重写规则，也成为生成规则，一般形式为 $α\rightarrowβ$ ，其中 $α 、 β$ 都是符号串， $α$ 至少含有一个 $V_n$ 中的符号。

语法 $G$ 的不含非终结符的句子形式称为 $G$ 生成的句子；
由语法 $G$ 生成的语言，记做 $L (G)$ ，指 $G$ 生成的所有句子的集合。

举个例子：
假设有一种语言 ${ab,aab,aaab,aaaab…\}$ ，如何用Chomsky形式文法表示？

从语言句子集合中我们可以看出，只有$ a、b$两种字符出现在句子集中，所以，终结符集合 $V_t=\{a,b\}$
我们有非终结初始符 $S$ ，假设非终结符集合 $V_n=\{S,A\}$ （ $V_n$ 中的元素个数、表示方法可以自己定义），我们可以将上述句子描述为：
$S\rightarrow Ab, \quad A\rightarrow aA, \quad A\rightarrow a$
也就是重写规则 $P$ 。
于是我们有语法：
$G=\{V_n,V_t,S,P\}$
其中，
$V_n = \{S,A\}$

$V_t=\{a,b\}$

$P:S\rightarrow Ab, \quad A\rightarrow aA|a$
（| 表示或）
于是，我们可以用有限的规则生成无限的语句。

值得注意的是， $G$ 的表示方法可能不唯一，以上例为例，将重写规则$ P$ 改为：
$P:S\rightarrow aA, \quad A\rightarrow aA, \quad A\rightarrow b$
这种语法也可以对该语言进行表示，大家可以自己推推看。

Chomsky根据重写规则的形式，将形式文法分为4级：

在这里，先加深一下集合的闭包这个概念：
$V^*$ 表示符号串集合 $V$ 的闭包，定义为： $V^*=V^0∪V^1∪V^2∪…$

举个例子：假设 $V=\{a,b\}$ ，那么
$V^0=\{\epsilon\},V^1=V,V^2=\{aa,ab,ba,bb\},V^*=\{\epsilon,a,b,aa,ab,ba,bb,aaa,…\}$

了解了这个概念之后，我们来介绍各级文法。

3.2 0型文法（无约束文法）

0型文法（无约束文法）： 重写规则为 $α\rightarrowβ$ ，其中， $α,β∈(V_n∪V_t)^*$ 。该文法对规则形式没有任何限制，因此也称为无约束文法或无限制重写文法。

3.3 1型文法（上下文相关文法）

1型文法（上下文相关文法）： 重写规则为 $αAβ\rightarrowαγβ$ ，其中， $A∈V_n,\quadα,β,γ∈(V_n∪V_t)^*$ ，且 $γ$ 非空。在上下文 $α . . . β$ 中，单个非终结符 $A$ 被重写为符号串 $γ$ , 因此是上下文相关的。

举个例子：
$G=\{V_n,V_t,S,P\}$ $V_n=\{S,A,B,C\},\quad V_t=\{a,b,c\}$ $P:S\rightarrow ABC,\quad A\rightarrow aA|a,\quad B\rightarrow bB|b,\quad BC\rightarrow Bcc$

容易判断，该文法属于1型文法，且 $\{a^nb^mc^2\},\quad n,m\ge1$

3.4 2型文法（上下文无关文法CFG）

2型文法（上下文无关文法CFG）： 重写规则为 $A\rightarrowα$ ，其中， $A∈V_n,\quadα∈(V_n∪V_t)^*$ ， $A$ 重写为 $α$ 时没有上下文限制。
举个例子：
$G=\{V_n,V_t,S,P\}$ $V_n=\{S,A,B,C\},\quad V_t=\{a,b,c\}$ $P:S\rightarrow ABC,\quad A\rightarrow aA|a,\quad B\rightarrow bB|b,\quad C\rightarrow BA|c$

容易判断，该文法属于2型文法，且 $\{a^nb^ma^pc^q\},\quad n,m\ge1,\quad p\ge0,\quad q∈\{0,1\}$ ，若 $p = 0$ ，则 $q = 1$ ；若 $p > 0$ ，则 $q = 0$

3.5 3型文法（正则文法RG）

3型文法（正则文法RG）： 重写规则为 $A\rightarrow Bx$ 或 $A\rightarrow x$ ，其中， $A,B∈V_n,\quad x∈V_t$ ； $A\rightarrow x$ 是将 $A\rightarrow Bx$ 中的 $B$ 看作空符号的一种特殊情况。如果把 $A, B$ 看作不同的状态，那么由重写规则可知，由状态 $A$ 转入状态 $B$ 时，可生成一个终结符 $x$ ，因此正则文法也称作有限状态文法。
上述定义的是左线性正则文法，如果 $A\rightarrow xB$ ，则是右线性正则文法。

举个例子：
$G=\{V_n,V_t,S,P\}$

$V_n=\{S,A,B,C\},\quad V_t=\{a,b\}$

$P:S\rightarrow aA,\quad A\rightarrow aA,\quad A\rightarrow bB,\quad B\rightarrow bC ,\quad C\rightarrow bC|b$

容易判断，该文法属于3型文法，且 $ L(G) = {a^nbm},\quad n\ge1,\quad m\ge3$

对上述4级文法有疑问的朋友可以私信给我，一同进行交流讨论~

此外，4级文法之间还有如图所示的关系：

$L(G_3)\subseteq L(G_2)\subseteq (G_1)\subseteq (G_0)$
即，每一个正则文法都是上下文无关文法，每一个上下文无关文法都是上下文有关文法，每一个上下文有关文法都是0型文法。
Chomsky把0型文法生成的语言叫0型语言，把由上下文有关文法、上下文无关文法、正则文法生成的语言分别叫作上下文有关语言、上下文无关语言、正则语言(或有限状态语言)。

一般来说，如果一种语言能由几种文法所产生，则把这种语言称为在这几种文法中受限制最多的那种文法所产生的语言。

4.自然语言形式文法

在NLP领域中，采用Chomsky形式文法作为刻画语言规律、表示语言的形式文法。
那么问题来了：用几型文法对自然语言进行刻画比较合适呢？
从描述能力上来说，正则文法描述能力太弱，上下文无关文法也不足以表述自然语言，因为自然语言中上下文相关情况非常常见。
然而，上下文有关文法的计算复杂度为NP完全，而上下文无关文法的复杂度为多项式复杂度，可以接受。
因此，用上下文无关文法来描述自然语言最为普遍，此外需要用一些其它手段来增强其描述能力。

上下文无关文法会产生二义性问题。
我们一定还记得这样一张歧义图：

对一个文法 $G$ ，如果存在某个句子有不只一棵分析树与其对应，那么称这个文法是二义的。
很明显，上下文无关文法处理语言会产生二义性。

Chomsky证明，任何由上下文无关文法生成的语言，均可由重写规则为 $A\rightarrow BC$ 或者 $A\rightarrow x$ 的文法生成，其中 $A,B,C∈V_n,\quad x∈V_t$ 。
具有这样重写规则的上下文无关文法，它的推导树均可简化为二元形式，这样就可以用二分法来分析自然语言，采用二叉树来表示自然语言的句子结构。
上述重写规则就称为 Chomsky范式。

之前我们提到过，Chomsky形式语言可以形式化表示为四元组：
$G = (V_n,V_t,S,P)$
那么，用它来表示自然语言，各部分究竟对应着什么呢？
$V_n$ ：非终结符的有限集合，对应语言语法单位（一般为“词” 戒“词组”的词性）。
$V_t$ ：终结符的有限集合，对应语言基本组成单位（一般为“词” ）
$V_n$ 中的初始符号，相当于语法范畴中的句子。
$P$ ：生成规则，对应语法结构规则（不同的语言有不同的规则），一般情况下由人工编写。

举个例子：
假设有如下语句：
{我吃饭，我洗衣，我喝水，我看书，
你吃饭，你洗衣，你喝水，你看书，
他吃饭，他洗衣，他喝水，他看书}

如何用形式文法表示？
$V_t =\{我，你，他，吃，洗，喝，看，饭，衣，书，水\}$

$V_n=\{S,IP,PR,VV,NN\}$

$P：S\rightarrow IP,\quad IP\rightarrow PR \quad VV \quad NN$

$PR\rightarrow 我|你|他,\quad VV\rightarrow 吃|洗|喝|看,\quad NN\rightarrow 饭|衣|书|水$

$G = \{V_n,V_t,S,P\}$

很明显，这是一个2型文法。

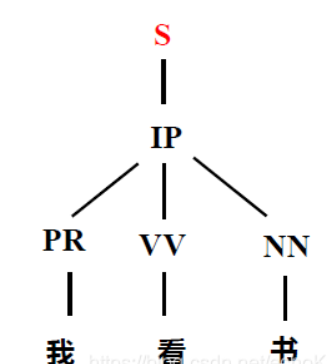
由此文法生成句子的过程图如下：

句子分析过程是生成过程的逆过程，由于形式文法中的生成规则是根据语法规则制定，所以在分析句子是否由某文法产生的同时就等同于对句子进行语法结构分析。

但是很明显的是，该种方法有很大的局限性：它局限于规则。
有很多句子无法由规则集生成（例如，我看你喝水），也有很多不合逻辑的句子可以由规则集生成（例如，我吃衣）。

在这一部分中，我们主要介绍了Chomsky形式文法，了解了如何利用它对自然语言进行表示；此外，我们还简单介绍了完全句法分析的概念。
在下一部分的内容中，我们将会对完全句法分析进行详细介绍，包括其所面临的问题和解决方法。

参考文献

[1] https://blog.csdn.net/echoKangYL/article/details/88106893

今天的文章句法结构乔姆斯基pdf_乔姆斯基的普遍语法理论分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/83888.html