前言
李宏毅2020机器学习的第一个作业是做PM2.5预测,模型用线性回归(linear regression),优化方法用梯度下降(gradient descent),要求手写。老师给了训练集(training set)和测试集(testing set)和参考代码,本文是在Pycharm上的实现的,pycharm上的环境搭建见另一篇博客,这个课程后期也用Pytorch。需要完整pycharm工程代码、数据集和测试结果等资料点击此处,没有积分的,可以私聊我,不过可能需要等我看到。理论见这篇博客
Pytorch版见:深度之眼pytorch打卡(四)| 台大李宏毅机器学习 2020作业(一):线性回归,实现多因素作用下的PM2.5预测(Pytorch版)
原理分析见:台大李宏毅 机器学习 2020学习笔记(二):回归与过拟合
数据集
- 训练集
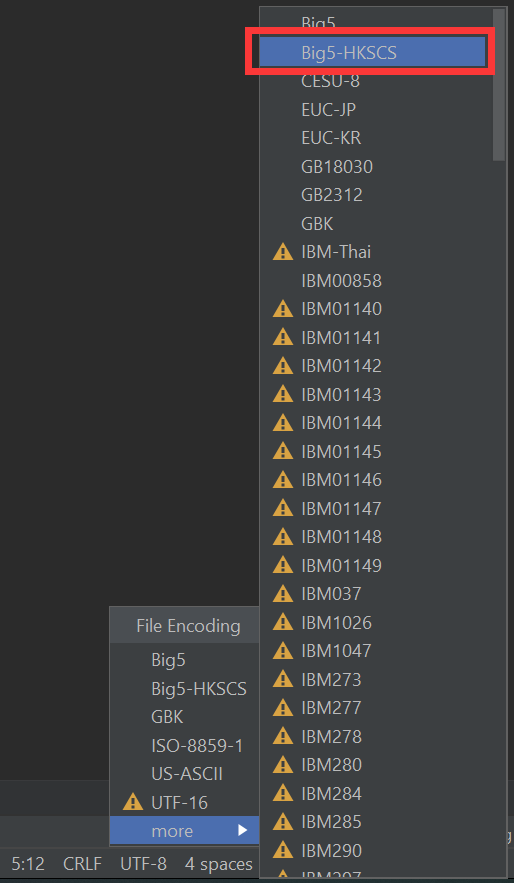
在网上下载的数据集编码方式是“big5”,繁体字的编码方式,下载后直接用excell打开会出现乱码。可以在Pycharm中打开,不过要先选择编码方式为“Big5-HKSCS”,再打开文件才不会出现乱码。正常打开文件之后,再选择编码方式为GBK,点击convert,则原来的文件就会变成GBK编码方式。
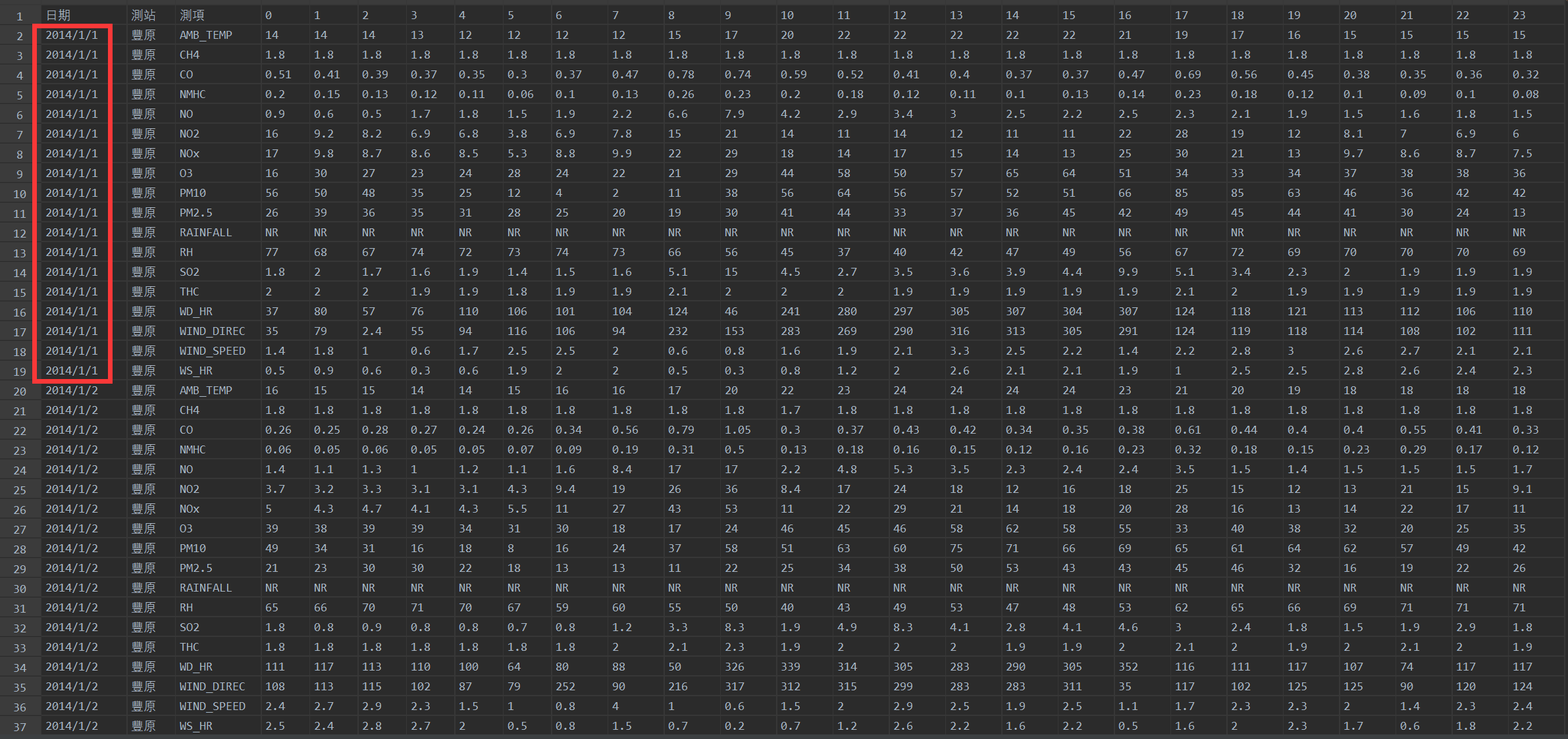
训练集包含2014年12个月中每个月取20天,每天24小时的环境监测数据,每个小时的数据都有18各特征,包括AMB_TEMP(温度), CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL(降雨量), RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR。部分训练集数据如下图。
- 测试集
测试集有训练集类似的格式,共240个id,每个id有9小时的数据,每组数据有18个特征。要求根据每个id前9个小时的所有数据来预测第10个小时的PM2.5值。
数据处理
主要参照老师给的参考文档
- 加载训练集并预处理
新建一个Pycharm工程,并在工程中建一个data文件夹用于存放数据。训练集中前三列为非数据内容,需要去掉,并且RAINFALL特征中的NR,即Not Rain 需要用数字0替换。
iloc:根据行列号来取数据。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('./data/train.csv', encoding='big5')
data = data.iloc[:, 3:] # 去掉前三列,即非数据列
data[data == 'NR'] = 0 # 将rainfall里的NR换成0,即不下雨为0
raw_data = data.to_numpy
# print(raw_data)- 训练集分组
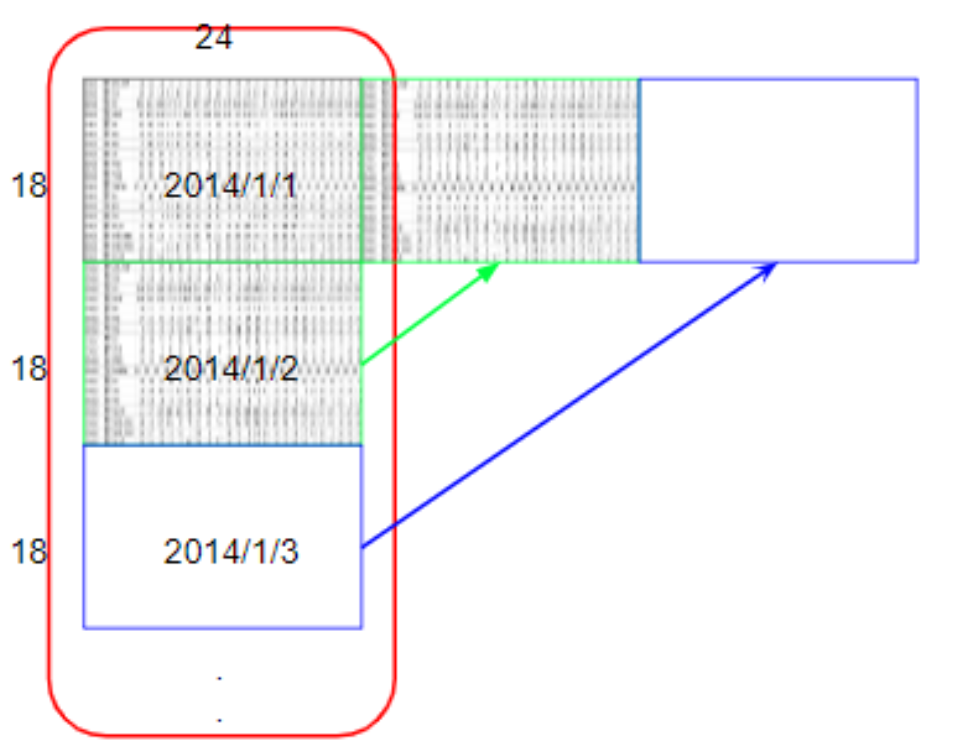
为了便于处理,先将每个月的资料由360*24的数据,转换成18*480的数据,如下图所示(图引自老师给的参考文档)。代码先将每个月的数据放到一个18*480的二维数组中,然后再将二维数组整体放入一个字典。最后生成的字典,以月份为索引,然后每个索引对应一个18*480的二维数组。
month_data = {}
for month in range(12):
sample = np.empty([18, 480])
for day in range(20):
sample[:, day*24:(day+1)*24] = raw_data[18*(day+20*month):18*(day+1+20*month), :] # 从一天的开始取到一天的结尾
month_data[month] = sample
# print(month_data)由于测试要求是根据前九个小时的数据推测出第十个小时的PM2.5值,所以再把10个小时的数据分为一组,其中前9个小时的18*9个特征作为输入x,第10个小时的第10个特征Pm2.5值作为输出y。采用步长为1的移动取值方式依次取10个值,如下图所示(图引自老师给的参考文档)则一月可取出(480-10)/1 +1=471组数据。那么一年就有12*471组数据。
reshape(1, -1):转换成一个行向量。
reshape(-1, 1) :转换成一个列向量。
参考文档在进行移位取值时用天和时间,这使的取值的参数变得很复杂,既然已经将一个月的数据合并,那么天与小时都已经是次要的信息。因此,此处对于1个月,只需要一个index,从0到471取到就可以了。
x = np.empty([12*471, 18*9], dtype=float)
y = np.empty([12*471, 1], dtype=float)
for month in range(12):
# 注释掉的部分为老师给的参考代码
# for day in range(20):
# for hour in range(24):
# if hour > 14 and day == 19: # 在每个月的结尾处,hour大于14后就没有一组数据了,即大于471小时
# continue
# x[month*471 + day*24 + hour, :] = month_data[month][:, day*20 + hour:day*20+hour+9].reshape(1, -1)
# # 以month值为索引,将每一组前9个小时的9*18的二维数组转换成一个9*18维的行向量,并赋值给x中的行
# y[month*471 + day*24 + hour, :] = month_data[month][9, day*20+hour+9]
# # 以month值为索引,将每一组第10个小时第10个特征,即PM2.5值给y的行
for index in range(471):
x[index+471*month, :] = month_data[month][:, index:index+9].reshape(1, -1)
y[index + 471 * month, :] = month_data[month][9, index + 9]
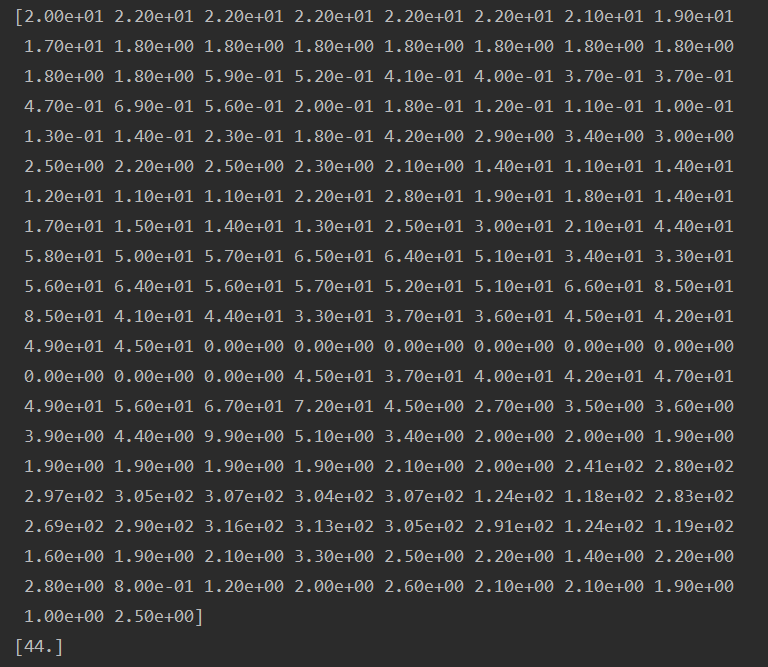
print(x[10])
print(y[10])对照x与训练集2014年1月1日10-18点内容,和y与19点的PM2.5值,可知是吻合的,代码没有问题。
-
训练集标准化(Normalize)
数据标准化之后模型更容易收敛,也更快收敛,方法就是让其减去均值再除以方差。
np.mean中,axis=0表示列均值,axis=1表示行均值。
mean_x = np.mean(x, axis=0) # 列均值
std_x = np.std(x, axis=0)
for i in range(len(x)):
for j in range(len(x[0])):
if std_x[j]!=0:
x[i][j] = (x[i][j]-mean_x[j])/std_x[j] # 每个元素减去其所在列的均值,再除以标准差
模型训练
模型:线性函数
输入:一次18*9个数据
参数:18*9个权重+一个偏置
损失函数:均方根误差(Root Mean Square Error)
优化算法:梯度下降、Adagrad
np.concatenate((a,b),axis=1) : 进行行拼接,拼接结果是[a,b]
np.dot(a,b):a与b点乘
np.power(a,b):a的b次方根
- 梯度下降法(BGD)优化
dim = 18*9 + 1
w = np.zeros([dim, 1])
x = np.concatenate((np.ones([12*471, 1]), x), axis=1).astype(float) # 为1那一列是bias前的系数
N = 12*471
learning_rate = 0.03
iter_time = 1000
loss = np.zeros([iter_time, 1])
for i in range(iter_time):
y1 = np.dot(x, w)
loss[i] = np.sqrt(np.sum(np.power(y1-y, 2))/N)
gradient = 2*np.dot(x.transpose(), y1-y)/N # 比原文,笔者在此处多除了个N,这样可以用更大的学习率
w = w - learning_rate*gradient
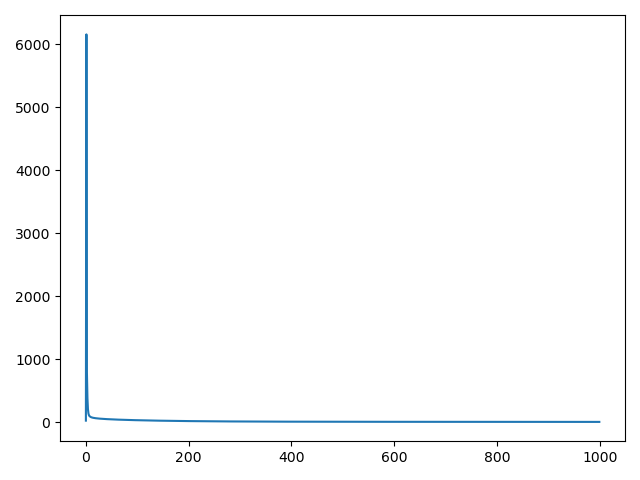
plt.plot(loss)
plt.show() 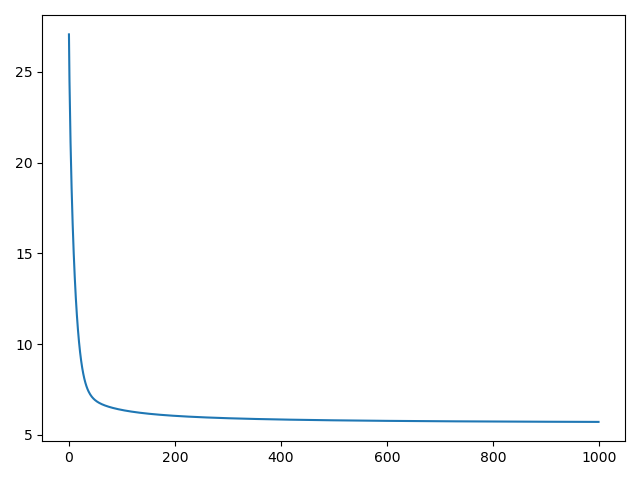
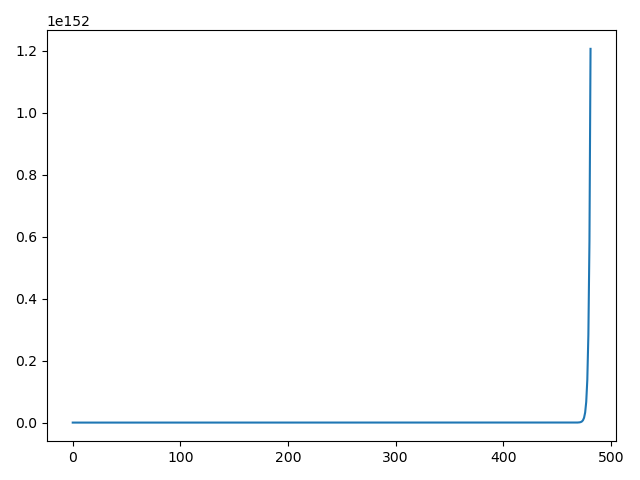
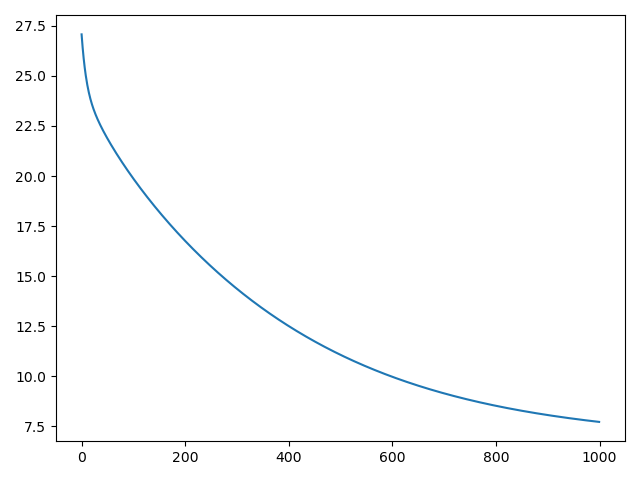
从左到右依次是0.03,0.05和0.001的学习率,迭代了1000次,较高的学习率无法收敛,较低的学习率收敛慢。
- Adagrad优化
比起BGD,这种优化方法,在更新参数时,除了乘学习率外,还除了过往所有梯度平方和的平方根,可动态的改变学习率。并且不会因为某时梯度太大而导致模型发散。
dim = 18*9 + 1
w = np.zeros([dim, 1])
x = np.concatenate((np.ones([12*471, 1]), x), axis=1).astype(float) # 为1那一列是bias前的系数
N = 12*471
learning_rate = 0.03
iter_time = 1000
loss = np.zeros([iter_time, 1])
adagrad = np.zeros([dim, 1])
eps = 0.000000001
for i in range(iter_time):
y1 = np.dot(x, w)
loss[i] = np.sqrt(np.sum(np.power(y1-y, 2))/N)
gradient = 2*np.dot(x.transpose(), y1-y)/N # 比原文,笔者在此处多除了个N,这样可以用更大的学习率
adagrad += gradient**2
w = w - learning_rate*gradient/np.sqrt(adagrad+eps) # eps为了防止分母为零的一个很小的数
plt.plot(loss)
plt.show()
np.save('weight.npy', w)
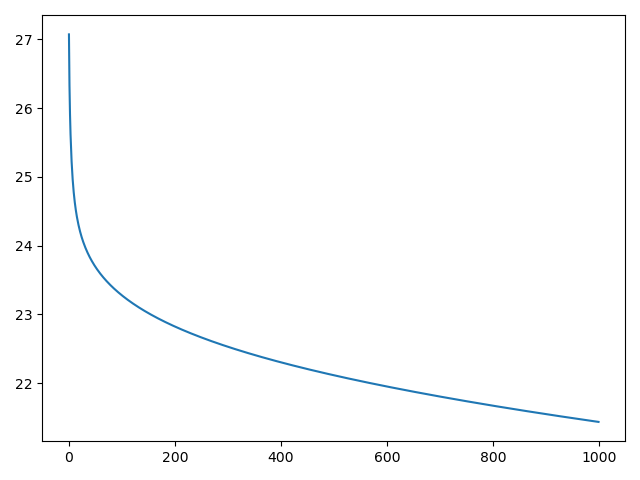
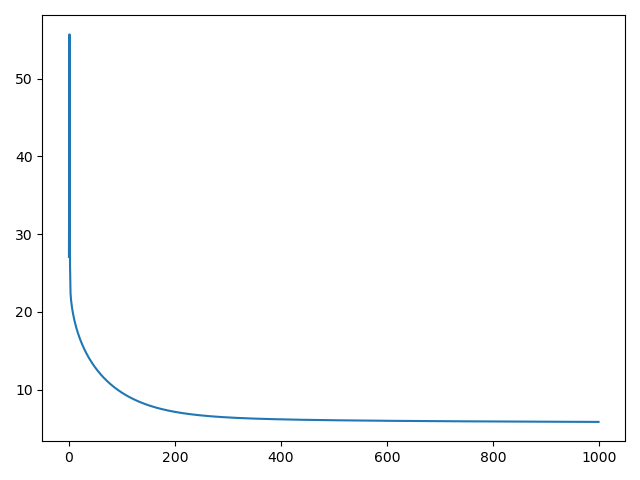
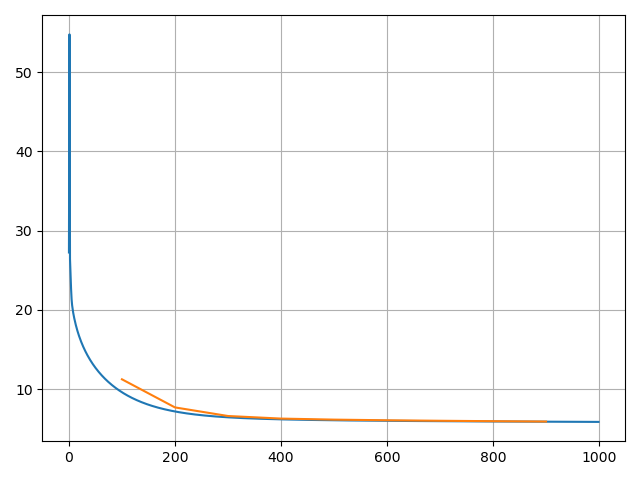
从左到右学习率是0.03,1,和100。
预测
由老师给的测试集,是没有第十个小时的,即相当于是直接预测,而不是测试。如果要做一下预测,可以从训练集从拿一个月的数据出来做测试集。
ValueError: could not broadcast input array from shape (153) into shape (162)
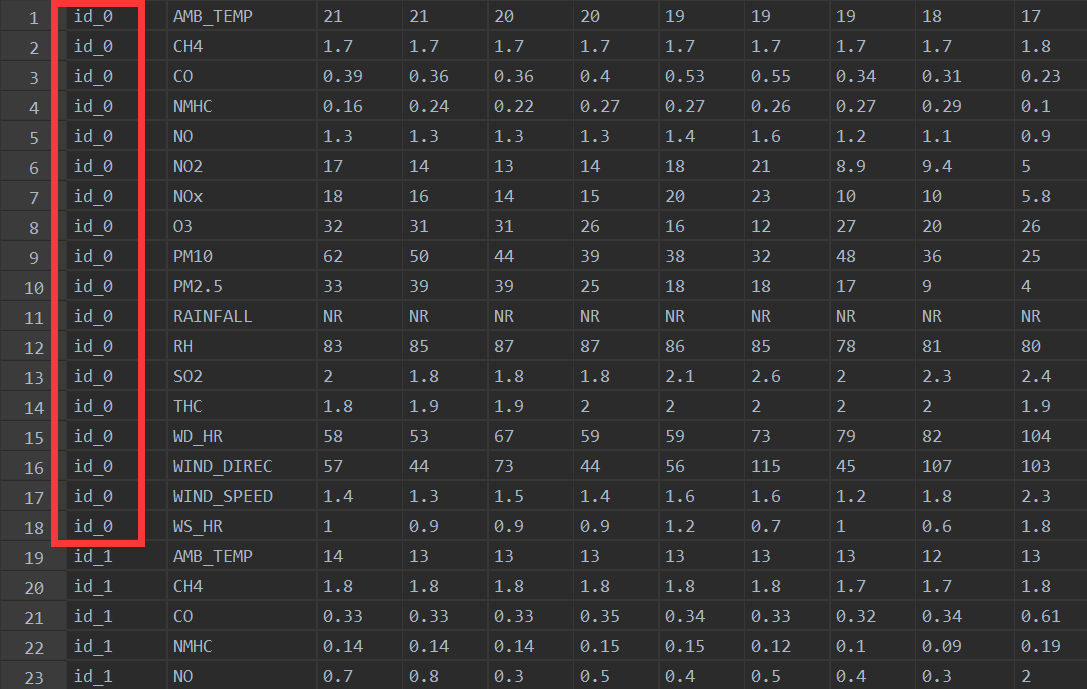
在处理测试集的时候出现这个错,是因为测试集没有列号,第一行就是数据,导致pd.read_csv将第一行数据当成了列号,因此数据少了一行。到最后就出现了维度对不上的错误。如图所示,本应该是4320*9。
test_data = pd.read_csv('./data/test.csv', encoding='big5', header=None) #加个header=None即可解决。
- 预测
数据的处理方式都与训练集相同,包括点乘生成y。由于预测的结果有负值,在输出时我将负值令成了0。
import csv
import pandas as pd
import numpy as np
test_data = pd.read_csv('./data/test.csv', encoding='big5', header=None)
test_data = test_data.iloc[:, 2:]
test_data[test_data == 'NR'] = 0
test_raw_data = test_data.to_numpy()
test_x = np.empty([240, 18*9], dtype=float)
# print(test_raw_data)
for i in range(240):
test_x[i, :] = test_raw_data[18 * i: 18 * (i + 1), :].reshape(1, -1)
# print(test_x[0])
test_mean = np.mean(test_x, axis=0)
test_std = np.std(test_x, axis=0)
for i in range(len(test_x)):
for j in range(len(test_x[0])):
if test_std[j] != 0:
test_x[i][j] = (test_x[i][j] - test_mean[j])/test_std[j]
# print(test_x[0])
test_x = np.concatenate((np.ones([240, 1]), test_x),axis=1).astype(float)
test_y = np.empty([240, 1], dtype=float)
w = np.load('weight.npy')
test_y = np.dot(test_x, w)
for i in range(240):
if int(test_y[i][0]) > 0:
print('id:', i, ' PM2.5:', int(test_y[i][0]))
else:
print('id:', i, ' PM2.5:', 0)
- 输出到CSV文件
with open('predict.csv', mode = 'w', newline='') as file:
csv_writer = csv.writer(file)
header = ['id', 'PM2.5']
csv_writer.writerow(header)
for i in range(240):
if int(test_y[i][0]) > 0:
row = ['id_'+str(i), str(int(test_y[i][0]))]
else:
row = ['id_'+str(i), '0']
csv_writer.writerow(row)由于没有正确答案 ,所以我将预测结果放在下面,有缘的人看到,实施之后可以比对结果。
| id | PM2.5 |
| id_0 | 2 |
| id_1 | 13 |
| id_2 | 18 |
| id_3 | 6 |
| id_4 | 21 |
| id_5 | 16 |
| id_6 | 17 |
| id_7 | 24 |
| id_8 | 13 |
| id_9 | 45 |
| id_10 | 11 |
| id_11 | 7 |
| id_12 | 47 |
| id_13 | 40 |
| id_14 | 16 |
| id_15 | 8 |
| id_16 | 24 |
| id_17 | 52 |
| id_18 | 0 |
| id_19 | 12 |
| id_20 | 33 |
| id_21 | 55 |
| id_22 | 7 |
| id_23 | 13 |
| id_24 | 11 |
| id_25 | 28 |
| id_26 | 10 |
| id_27 | 55 |
| id_28 | 5 |
| id_29 | 43 |
| id_30 | 17 |
| id_31 | 5 |
| id_32 | 2 |
| id_33 | 15 |
| id_34 | 22 |
| id_35 | 28 |
| id_36 | 33 |
| id_37 | 22 |
| id_38 | 35 |
| id_39 | 27 |
| id_40 | 4 |
| id_41 | 31 |
| id_42 | 24 |
| id_43 | 39 |
| id_44 | 12 |
| id_45 | 26 |
| id_46 | 19 |
| id_47 | 7 |
| id_48 | 18 |
| id_49 | 24 |
| id_50 | 18 |
| id_51 | 6 |
| id_52 | 14 |
| id_53 | 42 |
| id_54 | 12 |
| id_55 | 27 |
| id_56 | 24 |
| id_57 | 17 |
| id_58 | 44 |
| id_59 | 16 |
| id_60 | 13 |
| id_61 | 31 |
| id_62 | 8 |
| id_63 | 37 |
| id_64 | 10 |
| id_65 | 11 |
| id_66 | 9 |
| id_67 | 0 |
| id_68 | 33 |
| id_69 | 24 |
| id_70 | 15 |
| id_71 | 30 |
| id_72 | 46 |
| id_73 | 2 |
| id_74 | 13 |
| id_75 | 3 |
| id_76 | 31 |
| id_77 | 11 |
| id_78 | 16 |
| id_79 | 17 |
| id_80 | 20 |
| id_81 | 31 |
| id_82 | 17 |
| id_83 | 70 |
| id_84 | 28 |
| id_85 | 19 |
| id_86 | 18 |
| id_87 | 23 |
| id_88 | 19 |
| id_89 | 16 |
| id_90 | 23 |
| id_91 | 31 |
| id_92 | 2 |
| id_93 | 28 |
| id_94 | 36 |
| id_95 | 12 |
| id_96 | 27 |
| id_97 | 8 |
| id_98 | 18 |
| id_99 | 2 |
| id_100 | 13 |
| id_101 | 21 |
| id_102 | 8 |
| id_103 | 11 |
| id_104 | 17 |
| id_105 | 30 |
| id_106 | 23 |
| id_107 | 4 |
| id_108 | 6 |
| id_109 | 61 |
| id_110 | 36 |
| id_111 | 11 |
| id_112 | 22 |
| id_113 | 11 |
| id_114 | 10 |
| id_115 | 19 |
| id_116 | 18 |
| id_117 | 8 |
| id_118 | 13 |
| id_119 | 15 |
| id_120 | 65 |
| id_121 | 20 |
| id_122 | 27 |
| id_123 | 19 |
| id_124 | 6 |
| id_125 | 32 |
| id_126 | 8 |
| id_127 | 14 |
| id_128 | 21 |
| id_129 | 49 |
| id_130 | 17 |
| id_131 | 16 |
| id_132 | 47 |
| id_133 | 11 |
| id_134 | 12 |
| id_135 | 1 |
| id_136 | 8 |
| id_137 | 46 |
| id_138 | 16 |
| id_139 | 3 |
| id_140 | 21 |
| id_141 | 19 |
| id_142 | 34 |
| id_143 | 23 |
| id_144 | 14 |
| id_145 | 19 |
| id_146 | 8 |
| id_147 | 40 |
| id_148 | 18 |
| id_149 | 29 |
| id_150 | 6 |
| id_151 | 4 |
| id_152 | 18 |
| id_153 | 4 |
| id_154 | 10 |
| id_155 | 32 |
| id_156 | 5 |
| id_157 | 29 |
| id_158 | 7 |
| id_159 | 14 |
| id_160 | 31 |
| id_161 | 13 |
| id_162 | 8 |
| id_163 | 5 |
| id_164 | 39 |
| id_165 | 23 |
| id_166 | 0 |
| id_167 | 11 |
| id_168 | 49 |
| id_169 | 10 |
| id_170 | 50 |
| id_171 | 30 |
| id_172 | 19 |
| id_173 | 15 |
| id_174 | 48 |
| id_175 | 19 |
| id_176 | 15 |
| id_177 | 28 |
| id_178 | 8 |
| id_179 | 23 |
| id_180 | 12 |
| id_181 | 8 |
| id_182 | 44 |
| id_183 | 35 |
| id_184 | 13 |
| id_185 | 28 |
| id_186 | 20 |
| id_187 | 54 |
| id_188 | 7 |
| id_189 | 44 |
| id_190 | 28 |
| id_191 | 12 |
| id_192 | 23 |
| id_193 | 0 |
| id_194 | 14 |
| id_195 | 0 |
| id_196 | 26 |
| id_197 | 7 |
| id_198 | 13 |
| id_199 | 47 |
| id_200 | 18 |
| id_201 | 16 |
| id_202 | 50 |
| id_203 | 7 |
| id_204 | 6 |
| id_205 | 8 |
| id_206 | 6 |
| id_207 | 1 |
| id_208 | 96 |
| id_209 | 14 |
| id_210 | 11 |
| id_211 | 10 |
| id_212 | 27 |
| id_213 | 27 |
| id_214 | 14 |
| id_215 | 26 |
| id_216 | 58 |
| id_217 | 0 |
| id_218 | 9 |
| id_219 | 25 |
| id_220 | 12 |
| id_221 | 9 |
| id_222 | 88 |
| id_223 | 9 |
| id_224 | 12 |
| id_225 | 48 |
| id_226 | 13 |
| id_227 | 15 |
| id_228 | 6 |
| id_229 | 1 |
| id_230 | 35 |
| id_231 | 10 |
| id_232 | 40 |
| id_233 | 33 |
| id_234 | 18 |
| id_235 | 31 |
| id_236 | 52 |
| id_237 | 30 |
| id_238 | 12 |
| id_239 | 12 |
添加验证集
老师给的参考代码,将总的训练集的20%划分成了验证集,然后剩余的80%做的训练集。我打算把它既当做验证集也当做测试集来玩。
floor(x) :返回小于等于x的最大整数。
import math
train_x = x[:math.floor(len(x)*0.8), :]
train_y = y[:math.floor(len(x)*0.8), :]
val_x = x[math.floor(len(x)*0.8):, :]
val_y = y[math.floor(len(x)*0.8):, :]每100次迭代就用验证集验证一次,图中橙色线是其loss,注意到迭代完成模型的loss值还是有5.几,是很大的,可以发现线性模型并不能很好的拟合这个问题。
参考
https://colab.research.google.com/github/Iallen520/lhy_DL_Hw/blob/master/hw1_regression.ipynb
台大李宏毅机器学习 2020作业(一):手写线性回归,实现多因素作用下的PM2.5预测
https://www.bilibili.com/video/BV1LE411T7ns?p=1
资料网盘链接:链接:https://pan.baidu.com/s/1rfTlohQrjme8yhkYpPEMWQ 提取码:piex
今天的文章台大李宏毅机器学习 2020作业(一):手写线性回归,实现多因素作用下的PM2.5预测分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/84108.html