均值求解
本文介绍平均值、几何均值、调和均值、中位数、截尾法以及众值估计的求解方法,并用matlab对实例进行求解。
各值的特点
平均值
- 无系统误差和粗大误差时,直接求平均的结果最接近真值,用它来表示测量结果是最为可靠、简单的。
- 估计误差小,能反映出所有的数据特征。
- 易受到粗大误差的影响,属于非稳健估计。
- 计算简单
几何均值
- 表示平均增长率或变化率。
- 不具有最佳性、属于非稳健估计。
- 在实际运用中使用的不多
调和均值
- 一般用来分析数据含有某因素倒数的影响,如:平均密度、总平均速度、平均寿命等。
- 不具有最佳性、属于非稳健估计。
- 在实际运用中使用的不多。
中位数
- 对偏态数据的偏态不敏感。
- 估计误差比 x ˉ \bar{x} xˉ大。
- 不能反映出数据的全部信息,但是也因此有较好的稳健性。
- 计算复杂(需要排序)。
截尾法均值
- 特性介于均值与中位数之间,拥有两者共同的优缺点。
- 可以弥补均值的非稳健性和中位值的效率低的特点。
- 属于稳健估计法。
- 经验表明一般情况截去数据中最小的10%和最大的%10.
众值
- 仅可以反映出现次数最多的数据信息,丢失的信息较多。
- 多峰分布下,难以确定众值或众值偏差较大。
- 估计误差和统计特性难以分析。
- 实际应用较少。
编程求解
问题
对某真值为5的数据进行8次测量,测量值分别为:5.001, 5.002, 4.998, 4.993, 5.001, 5.008, 5.500, 4.997.试分别采用最小二乘(平均值)、几何均值、调和均值、中位数、截尾法以及众值估计这组测量数据的测量值,并比较优缺点。
matlab求解
题目要求用多种指标:平均值、几何均值、调和均值、中位数、截尾法以及众值估计测量数据的真值,并用偏差、计算量等指标分析各个估计方法的优缺点。
将题目所给的数据输入matlab,编程求解各个待求量,程序如下:
clear;clc;
%edit by callmiaoup
%data 2021-4-20
%Ver 1.0
data=[5.001,5.002,4.998,4.993,5.001,5.008,5.500,4.997]; %输入数据
ave=(sum(data)/length(data)); %平均值
geoave=(data(1)*data(2)*data(3)*data(4)*data(5)*data(6)*data(7)*data(8))^(1/length(data)); %几何均值
reconcileave=1/(1/data(1)+1/data(2)+1/data(3)+1/data(4)+1/data(5)+1/data(6)+1/data(7)+1/data(8))*length(data); %调和均值
sort=sort(data); %排序
mid=(sort(length(data)/2)+sort(length(data)/2+1))/2; %中位数
truncation=(sort(2)+sort(3)+sort(4)+sort(5)+sort(6)+sort(7))/(length(data)-2); %截尾法
mode=mode(data); %众值
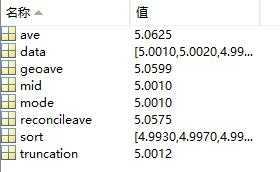
运行结果如图:
使用tic-toc命令可以查看各个数据求解的耗时,将其加上。运行程序。
结果分析
将实测结果用表格的形式列出来:
| 均值类型 | 结果 | 绝对误差 | 相对误差 | 误差排序 | 耗时(us) | 耗时排序 |
|---|---|---|---|---|---|---|
| 最小二乘均值 | 5.0625 | 0.0625 | 1.25% | 6 | 97 | 3 |
| 几何均值 | 5.0599 | 0.0599 | 1.20% | 5 | 175 | 5 |
| 调和均值 | 5.0575 | 0.0575 | 1.15% | 4 | 129 | 4 |
| 中位数 | 5.001 | 0.001 | 0.02% | 1 | 78 | 1 |
| 截尾法均值 | 5.0012 | 0.0012 | 0.02% | 3 | 86 | 2 |
| 众值 | 5.001 | 0.001 | 0.02% | 1 | 211 | 6 |
由表格可以分析出:从计算精度来看,对比求平均的计算结果和真实值,误差有小到高的算法分别为:众值、中位数、截尾均值、调和均值、几何均值、最小二乘(平均值)。其中中位数和众值误差在所有方法的对比中最低,为0.02%.
从计算耗时来看,中位数耗时最短,其次是截尾法均值,但是这两种方法在测量耗时时均为将数据升序排列的时间计算其中,所以一段样本在未经处理时,中位数和截尾法均值的计算时长是不短的。其次是最常用的平均值,耗时在100us以内。耗时最长的是众值,在程序求解众值时,因为需要不短搜索与储存出现次数最多的数值,所以对于计算能力和存储空间的要求都较高,这也是众值在实际运用中不常采用的原因之一。
总结
随机误差影响下测量数据表现为某种随机变量,其分布中心位置理论上可用期望值(数学期望/均值)表征。求均值的方法很多,使用的领域和不尽相同,没有绝对好于绝对不好的方法,我们需要在实际使用时找到最适合当前数据的均值。
今天的文章平均值众数中位数作用_matlab中位数怎么求「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/84407.html