1. 编程号首页

模糊矩阵计算详细例题_数学建模求最优解的算法

编程小号 • • 未分类

模糊矩阵计算详细例题_数学建模求最优解的算法本文介绍了Gurobi的各种建模方式，包括按行建模、按列建模、按非零元素建模以及按矩阵形式建模

优化求解器 | Gurobi的MVar类：矩阵建模利器、求解对偶问题的备选方案

作者：刘兴禄，清华大学，清华-伯克利深圳学院博士在读
修宇璇，清华大学，清华-伯克利深圳学院博士在读

欢迎关注我们的微信公众号 运小筹

在这里插入图片描述

本文涉及到的模型(LP, MIP)均是为了说明问题，即使是MIP，我们也将其当做LP看待。

  • LP: linear programming, 线性规划；
  • MIP: mixed integer programming, 混合整数(线性)规划。

优化求解器的建模方式：以gurobi为例

我们考虑如下的线性规划问题
 Maximize  Z = 3 x 1 + 5 x 2  subject to  x 1 ≤ 4 2 x 2 ≤ 12 3 x 1 + 2 x 2 ≤ 18  and  x 1 ≥ 0 , x 2 ≥ 0 \begin{array}{l}\text { Maximize } \quad Z=3 x_{1}+5 x_{2} \\ \text { subject to } \\ \quad \begin{aligned} x_{1} \quad \leq 4 \\ 2 x_{2} \leq 12 \\ 3 x_{1}+2 x_{2} \leq 18 \\ \text { and } \quad x_{1} \geq 0, \quad x_{2} \geq 0 \end{aligned}\end{array}  Maximize Z=3x1​+5x2​ subject to x1​≤42x2​≤123x1​+2x2​≤18 and x1​≥0,x2​≥0​​

该模型有2个决策变量 x 1 x_1 x1​和 x 2 x_2 x2​，3个约束。

如果我们使用Gurobi对其进行建模，一般有下面3（或者说4）种方法：

  1. 按行建模：逐行进行建模。通过使用quicksum或者创建表达式LinExpr对象结合addTerms，拼凑表达式，最后使用Model.addConstr完成添加约束的操作，从而完成建模；
  2. 按列建模：逐列进行建模。通过创建Column对象，使用addTerms函数拼凑好Column对象，最后使用Model.addVar函数直接完成建模。
  3. 按非零系数建模：类似于逐列进行建模，可以使用addTerms拼凑表达式。具体实现跟按行建模类似。
  4. 按矩阵方式建模：通过拼凑约束系数矩阵 A A A，然后将决策变量转化为MVar的对象，最后直接使用重载运算符@完成约束的添加，即如Model.addConstr(A @ x == b)，就可以完成建模。

前3中建模方法我们已经在之前的推文中有所涉及，见推文：

本文主要来介绍第四种:按矩阵方式建模.。主要内容包括：

  1. 按矩阵方式建模的详细案例和代码；
  2. 按矩阵方式建模，并通过求解器轻松得到对偶问题的例子和代码。

在介绍具体内容之前，笔者首先指出按照矩阵建模的好处和不足：

优点：

  1. 添加约束代码量少，只需要拼凑好系数矩阵，即可一行代码搞定约束的添加；
  2. 便于直接得到对偶问题的系数矩阵( A T A^{T} AT)，从而快速得到对偶问题的具体形式。

缺点：

  1. 对于约束系数稀疏的模型，会占用不必要的内存来存储那些系数为0的部分，模型较大时，有可能导致内存溢出；
  2. 虽然可以得到对偶问题的具体形式，但是对偶问题的公式形式却不能得出（这个严格来讲不算是这种建模方式的缺点）。
  3. 不方便对每个决策变量赋予独一无二的变量名。

Gurobi提供了矩阵形式建模的API，下面我们就基于上述小例子来介绍Gurobi的矩阵建模。

Gurobi的MVar（矩阵形式变量对象）

Gurobi的MVar可以查看手册中的相关内容：

https://www.gurobi.com/documentation/9.5/refman/py_mvar.html

这里我们将Gurobi用户手册中关于MVar和@的部分拿过来供大家参考：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

注意：根据上图，@运算符也可以用于创建二次表达式以及添加二次表达式。例如x @ Q @ y <= 3。

关于二次矩阵表达式的详细介绍，我们日后再谈，本文仅简要涉及。

下面我们来看本文要详细介绍的例子。

一个线性规划的例子：Wyndor玻璃厂

在本文中，我们采用Introduction to Operations Research里一个经典的线性规划的例子：Wyndor玻璃厂问题。

该问题的描述如下：

Wyndor玻璃厂的产品包括窗户和玻璃门。 它有三个工厂：

  1. 铝制框架和五金件在第一工厂生产;
  2. 木质框架在第二工厂生产;
  3. 第三工厂生产玻璃并组装产品。

由于收益下降，高层管理人员决定对公司的产品线进行改造，腾出生产能力，推出两种具有巨大销售潜力的新产品。

  • 产品1：一个8英尺的玻璃门，铝制框架。
  • 产品2：一种4×6英尺的双挂木质框架窗。

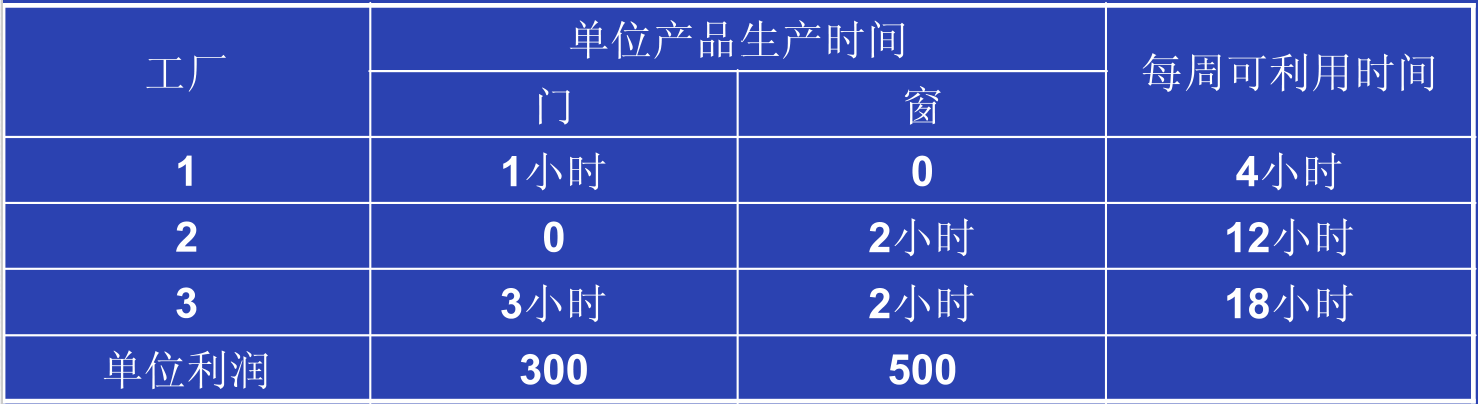
产品1需要1号和3号工厂的部分产能，但不需要2号工厂的产能。产品2只需要工厂2和3。市场部门得出的结论是，该公司生产多少就能销售多少。然而，由于这两种产品产品将竞争3号厂的产能，因此需要决定两种产品的最优，以使得利润最大化。

具体的数据如下表所示：

模糊矩阵计算详细例题_数学建模求最优解的算法

问题的建模

我们引入如下2个决策变量：

  • x 1 x_1 x1​: 生产产品1的数量；
  • x 2 x_2 x2​: 生产产品2的数量。

则原问题可以建模为如下的整数规划(但是为了后续介绍方便，我们姑且将其松弛，认为产品个数可以是小数，因此问题变成了线性规划)：
 Maximize  Z = 3 x 1 + 5 x 2  subject to  x 1 ≤ 4 2 x 2 ≤ 12 3 x 1 + 2 x 2 ≤ 18  and  x 1 ≥ 0 , x 2 ≥ 0 \begin{array}{l}\text { Maximize } \quad Z=3 x_{1}+5 x_{2} \\ \text { subject to } \\ \quad \begin{aligned} x_{1} \quad \leq 4 \\ 2 x_{2} \leq 12 \\ 3 x_{1}+2 x_{2} \leq 18 \\ \text { and } \quad x_{1} \geq 0, \quad x_{2} \geq 0 \end{aligned}\end{array}  Maximize Z=3x1​+5x2​ subject to x1​≤42x2​≤123x1​+2x2​≤18 and x1​≥0,x2​≥0​​
写成矩阵形式：
 Maximize  Z = [ 3 , 5 ] [ x 1 x 2 ]  subject to  [ 1 0 0 2 3 2 ] [ x 1 x 2 ] ≤ [ 4 12 18 ]  and  [ x 1 x 2 ] ≥ [ 0 0 ] \begin{array}{l}\text { Maximize } \quad Z=[3,5]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \\ \text { subject to } \\ \qquad\left[\begin{array}{ll}1 & 0 \\ 0 & 2 \\ 3 & 2\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \leq\left[\begin{array}{r}4 \\ 12 \\ 18\end{array}\right] \\ \text { and } \quad\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right] \geq\left[\begin{array}{l}0 \\ 0\end{array}\right]\end{array}  Maximize Z=[3,5][x1​x2​​] subject to ⎣⎡​103​022​⎦⎤​[x1​x2​​]≤⎣⎡​41218​⎦⎤​ and [x1​x2​​]≥[00​]​

为了简化符号，我们令
c = [ 3 5 ] x = [ x 1 x 2 ] A = [ 1 0 0 2 3 2 ] b = [ 4 12 18 ] \begin{aligned} &\mathbf{c}=\left[ \begin{array}{c} 3\\ 5\\ \end{array} \right] \\ &\mathbf{x}=\left[ \begin{array}{c} x_1\\ x_2\\ \end{array} \right] \\ &\mathbf{A}=\left[ \begin{matrix}{} 1& 0\\ 0& 2\\ 3& 2\\ \end{matrix} \right] \\ &\mathbf{b}=\left[ \begin{array}{r} 4\\ 12\\ 18\\ \end{array} \right] \end{aligned} ​c=[35​]x=[x1​x2​​]A=⎣⎡​103​022​⎦⎤​b=⎣⎡​41218​⎦⎤​​

上述模型可以写为下面更紧凑的矩阵形式
max ⁡ c T x s.t. A x ⩽ b , x ⩾ 0. \begin{aligned} \max \quad & \mathbf{c}^{T}\mathbf{x} \\ \text{s.t.} \quad &\mathbf{A}\mathbf{x} \leqslant \mathbf{b}, \\ & \mathbf{x} \geqslant \mathbb{0}. \end{aligned} maxs.t.​cTxAx⩽b,x⩾0.​

基于Gurobi进行按矩阵形式建模：完整代码

我们用矩阵形式对上述模型进行建模。用到的函数为Gurobi内部定义的重载运算符@， @是Gurobi内部定义的矩阵运算符，用来计算一个约束矩阵和一系列决策变量组成的MVar的矩阵相乘。

例如，系数矩阵为 A ∈ R 2 × 3 \mathbf{A} \in \mathbb{R}^{2\times 3} A∈R2×3，决策变量 x \mathbf{x} x为 1 × 3 1\times 3 1×3的MVar对象， 则它们的乘积可以表示为
A @ x \begin{aligned} \mathbf{A} @ \mathbf{x} \end{aligned} A@x​

需要用到的函数：

  • Model.addMVar(shape, lb=0, ub=GRB.INFINITY, obj=0.0, vtype=GRB.CONTINUOUS, name="")，其中shape是一个标量，表示决策变量的个数。

注意，使用重载运算符 @的时候， x \mathbf{x} x必须为MVar对象。

下面是求解原始问题的代码：

import gurobipy as grb
import numpy as np

if __name__ == "__main__":
    m = grb.Model("LP")
    m.setParam('OutputFlag', 1)
    
    x = m.addMVar(2, lb=0, ub=grb.GRB.INFINITY)
    
    c = np.array([[3, 5]])
    A = np.array([[1, 0],
                  [0, 2],
                  [3, 2]])
    b = np.array([4, 12, 18])
    
    m.addConstr(A @ x <= b)
    
    m.Params.timelimit = 9999999999999999999999
    
    m.setObjective(c @ x, grb.GRB.MAXIMIZE)
    
    m.update()
    m.optimize()
    print('x_1={}'.format(x[0].x))
    print('x_2={}'.format(x[1].x))

结果：

Presolve removed 2 rows and 0 columns
Presolve time: 0.01s
Presolved: 1 rows, 2 columns, 2 nonzeros

Iteration    Objective       Primal Inf.    Dual Inf.      Time
       0    4.5000000e+01   1.500000e+00   0.000000e+00      0s
       1    3.6000000e+01   0.000000e+00   0.000000e+00      0s

Solved in 1 iterations and 0.02 seconds (0.00 work units)
Optimal objective  3.600000000e+01
x_1=2.0
x_2=6.0

我们导出模型，查看一下模型的具体形式：

m.write('model.lp')

导出的模型如下：

\ Model LP
\ LP format - for model browsing. Use MPS format to capture full model detail.
Maximize
  3 C0 + 5 C1
Subject To
 R0: C0 <= 4
 R1: 2 C1 <= 12
 R2: 3 C0 + 2 C1 <= 18
Bounds
End

确实是正确的模型。

将Var对象转成MVar对象

上面提到，当使用m.addConstr(A @ x <= b)类似的语句的时候， x \mathbf{x} x必须为MVar对象。

但是如果我们一开始使用的是Model.Vars()建模的，可不可以也使用m.addConstr(A @ x <= b)这样的语言来建模呢？

答案是：可以的，但是需要将Var对象转换成MVar对象。

下面是一个例子：


from gurobipy import *
import numpy as np

model = Model()

A = np.ones([2, 2])
A[0][0] = 2
A[1][1] = 3
''' A = [ [2, 1], [1, 3] ] '''

b = np.ones([2, 1])

x = model.addVars(2, 1, vtype=GRB.BINARY)

model.update()

x = MVar(model.getVars())

model.addConstr(A @ x == 1)

model.write('A.lp')
print(A)

在上面的例子中，我们首先利用Model.Vars()创建了Var变量对象，然后使用x = MVar(model.getVars())将变量转换成了MVar对象，这样就可以顺利使用按照矩阵方式建模了。

Model.getA()函数的使用

Gurobi提供了一个可以得到模型的约束系数矩阵的函数Model.getA()。我们来测试一下该函数：

    A = m.getA()
    print('A: ', A)
    print('type A: ', type(A))

结果如下：

A： (0, 0)	1.0
   (1, 1)	2.0
   (2, 0)	3.0
   (2, 1)	2.0
type A： <class 'scipy.sparse.csr.csr_matrix'>

基于矩阵形式建模的对偶问题的书写及建模

根据对偶理论，上述模型的对偶问题可写成：

min ⁡ b T y s.t. A T y ⩽ c , y ⩾ 0. \begin{aligned} \min \quad & \mathbf{b}^{T}\mathbf{y} \\ \text{s.t.} \quad &\mathbf{A}^{T}\mathbf{y} \leqslant \mathbf{c}, \\ & \mathbf{y} \geqslant \mathbb{0}. \end{aligned} mins.t.​bTyATy⩽c,y⩾0.​

其中
y = [ y 1 y 2 y 3 ] \begin{aligned} \mathbf{y}=\left[ \begin{array}{r} y_1\\ y_2\\ y_3\\ \end{array} \right] \end{aligned} y=⎣⎡​y1​y2​y3​​⎦⎤​​

其具体形式为：
 Minimize  W = 4 y 1 + 12 y 2 + 18 y 3  subject to  y 1 + 3 y 3 ≥ 3 2 y 2 + 2 y 3 ≥ 5 y 1 ≥ 0 , y 2 ≥ 0 , y 3 ≥ 0 \begin{array}{l}\text { Minimize } \quad W=4 y_{1}+12 y_{2}+18 y_{3} \\ \text { subject to } \\ \qquad \begin{aligned} y_{1} &+3 y_{3} \geq 3 \\ 2 y_{2} &+2 y_{3} \geq 5 \\ y_{1} \geq 0, & y_{2} \geq 0, \quad y_{3} \geq 0 \end{aligned}\end{array}  Minimize W=4y1​+12y2​+18y3​ subject to y1​2y2​y1​≥0,​+3y3​≥3+2y3​≥5y2​≥0,y3​≥0​​

对偶问题的矩阵具体形式为：

 Minimize  w = [ y 1 , y 2 , y 3 ] [ 4 12 18 ]  subject to  [ y 1 , y 2 , y 3 ] [ 1 0 0 2 3 2 ] ≥ [ 3 , 5 ]  and  [ y 1 y 2 y 3 ] ≥ [ 0 0 0 ] \begin{array}{l}\text { Minimize } w=\left[y_{1}, y_{2}, y_{3}\right]\left[\begin{array}{r}4 \\ 12 \\ 18\end{array}\right] \\ \text { subject to } \\ {\left[y_{1}, y_{2}, y_{3}\right]\left[\begin{array}{ll}1 & 0 \\ 0 & 2 \\ 3 & 2\end{array}\right] \geq[3,5]}\\ \text { and } \quad\left[\begin{array}{l}y_{1} \\ y_{2}\\y_{3}\end{array}\right] \geq\left[\begin{array}{l}0 \\ 0\\0\end{array}\right] \end{array}  Minimize w=[y1​,y2​,y3​]⎣⎡​41218​⎦⎤​ subject to [y1​,y2​,y3​]⎣⎡​103​022​⎦⎤​≥[3,5] and ⎣⎡​y1​y2​y3​​⎦⎤​≥⎣⎡​000​⎦⎤​​

基于Gurobi进行按矩阵形式进行对偶问题的建模并求解

在矩阵建模的方式下，我们实现对偶问题的建模非常简单，只需要按照上一节的介绍，将原问题的系数矩阵 A \mathbf{A} A转置，得到 A T \mathbf{A}^{T} AT，并且创建对偶问题的决策变量 y \mathbf{y} y，然后就可以轻松完成对偶问题的建模。具体代码如下。

if __name__ == "__main__":
    m = grb.Model("LP")
    m.setParam('OutputFlag', 1)
    y = m.addMVar(3, lb=0, ub=grb.GRB.INFINITY)
    c = np.array([3, 5])
    A = np.array([[1, 0],
                  [0, 2],
                  [3, 2]])
    b = np.array([4, 12, 18])
    
    m.addConstr(A.T @ y >= c)
    
    m.Params.timelimit = 9999999999999999999999
    
    m.setObjective(b @ y, grb.GRB.MINIMIZE)
    
    m.update()
    m.optimize()
    print('y_1={}'.format(y[0].x))
    print('y_2={}'.format(y[1].x))
    print('y_3={}'.format(y[2].x))

求解结果如下：

Presolve time: 0.00s
Presolved: 2 rows, 3 columns, 4 nonzeros

Iteration    Objective       Primal Inf.    Dual Inf.      Time
       0    0.0000000e+00   3.250000e+00   0.000000e+00      0s
       2    3.6000000e+01   0.000000e+00   0.000000e+00      0s

Solved in 2 iterations and 0.00 seconds (0.00 work units)
Optimal objective  3.600000000e+01
y_1=0.0
y_2=1.5
y_3=1.0

我们将对偶问题的模型导出查看：

m.write('dual.lp')

\ Model LP
\ LP format - for model browsing. Use MPS format to capture full model detail.
Minimize
  4 C0 + 12 C1 + 18 C2
Subject To
 R0: C0 + 3 C2 >= 3
 R1: 2 C1 + 2 C2 >= 5
Bounds
End

可见是完全吻合的。

小结

本文介绍了Gurobi的各种建模方式，包括按行建模、按列建模、按非零元素建模以及按矩阵形式建模.

我们详细介绍了按矩阵形式建模的案例及其在快速完成对偶问题建模中的使用。

但是笔者还是需要说明一点：按矩阵形式建模，虽然可以很方便地用求解器完成对偶问题的建模，但是如果科技论文中，需要大家写出对偶问题的具体公式形式，则这种方法不再奏效。从利用求解器实现对偶问题的求解角度来讲，本文介绍的办法完全没有问题。但是还是鼓励大家直接将对偶问题的具体公式形式写出来，这样对今后的研究更有好处。

参考资料

  1. Gurobi Optimizer Reference Manual-9.5.1
  2. Hillier F S. Introduction to operations research[J]. 1967.

今天的文章模糊矩阵计算详细例题_数学建模求最优解的算法分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/84508.html

赞 (0)
编程小号编程小号
0

相关推荐

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注