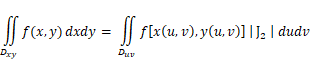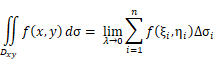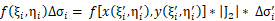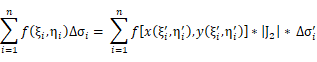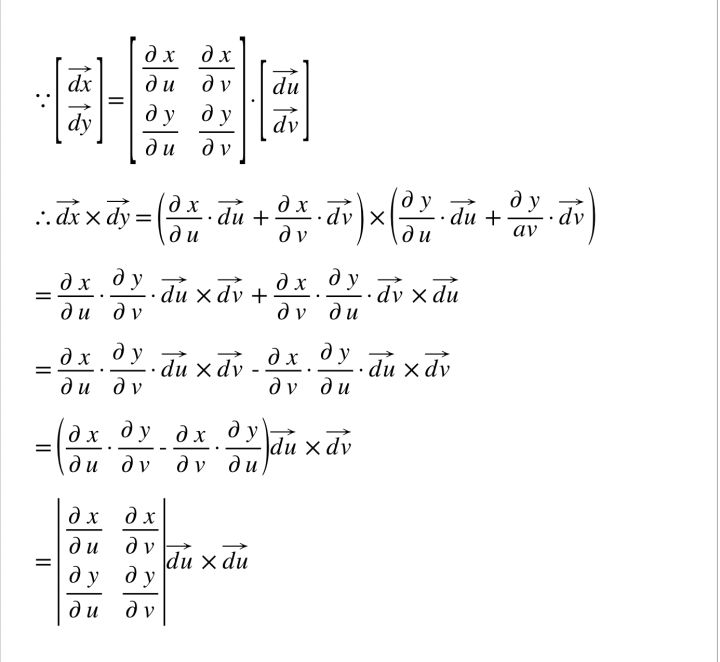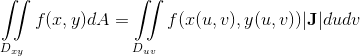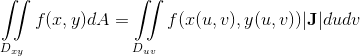我们以二重积分为例进行说明,首先说结论:
一、结论
若x = x(u, v), y = y(u, v)存在偏导数,则二阶雅可比行列式为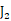
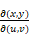
dxdy = |J2| dudv, (J2的绝对值),且
其中积分区域

二、理解
二重积分的定义中指出,将积分区域
其中Δσi表示第i个小闭合区域的面积,在闭合区域上取一点(ξi, ηi), 这一点的函数值与区域Δσi的乘积的总和为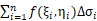
dσ为小闭合区域的面积,假设我们将Dxy分隔为一个一个小矩形区域,每一小块积分区域Δσi 在uv坐标系中都对应一块积分区域Δσi’,它们是一一对应的,并且Δσi=|J2|Δσi’,|J2| 是雅可比行列式的绝对值,可能是常量,但一般情况下是一个变量,所以我们可以保证以下等式成立:
在xy坐标系中第i块积分区域上任取一点(ξi, ηi),都能在uv坐标系中的第i块积分区域中找到一点(ξi‘,ηi’),并满足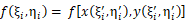
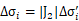
‘
故,两边取极限,二重积分也就相等,即一中结论成立。
下面我们主要说明为什么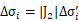
解释1
首先我们应该怎么理解dxdy,在xy坐标系中,dx和dy可以看成是小矩形的长和宽,它们相互垂直,dxdy可以简单的理解为两个标量相乘求面积,用来代替Δσi,但是在uv坐标系中,du和dv相互垂直,但是dx和dy代表的是一个平行四边形的两条边,并不垂直,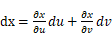
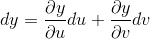
图一:
两边取模,dxdy = |J2|dudv
https://www.zhihu.com/question/274450639,
另外也可以参考MIT的微积分课程:
https://open.163.com/movie/2010/8/G/2/M6TUC9K75_M6TUID0G2.html,
18课24分钟,更简单的描述过程。
其实在xy坐标系中我们也可以将dxdy理解为向量叉乘的模,只不过他们夹角是90度,所以等于标量乘积。
注:以上描述非常可能是错误的,并没有参考正规资料,只是一个知乎网友提供的描述(见上述链接),我并不确定是否能把dxdy、dudv写成向量的形式,所以请批判性的参考,而且,我无法解释为什么最终du dv两个向量取模没有乘以其夹角的正弦值,如果上述是完全是错误的那么我们只能用面积比值强行解释了:
解释2
参考:https://wenku.baidu.com/view/f56aa732b94ae45c3b3567ec102de2bd9605de8b
我们将积分区域Dxy按照上图右进行划分成N多个小块,根据微积分的定义,计算结果和微分方式无关,所以我们把它为分成这种扭曲的方式,每一个扭曲的小块一一对应uv坐标系中每一个规则的矩形,切他们的面积比值为|J|,也就是dA = |J|dudv
由于积分的计算结果与积分区域的划分方式无关,所以,其中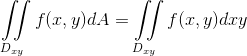
以下是上上次编辑此篇博客时留下的,但是没有图,可以忽略。
下面通过 直观的解释来理解为什么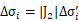
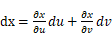
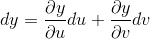
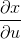
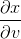

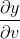
今天的文章二重积分和雅可比行列式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/8468.html