rlc阻抗计算公式_RLC并联电路阻抗表达式

一、RLC（串联）电路的阻抗

如果一个电路由R1、R2、R3组成，那么它的电阻是不是很容易计算？如下图中的R = R1 + R2 + R3。

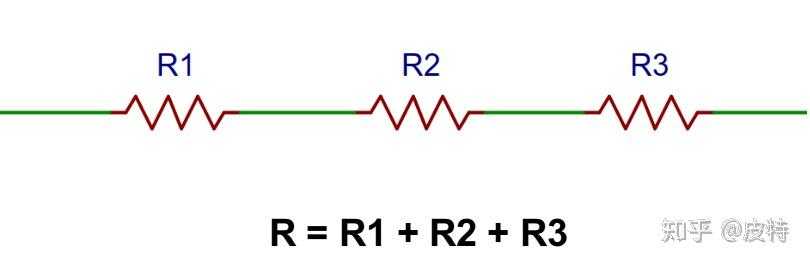
如果一个电路由R、L、C组成，那么它的阻抗是多少？难道也是电阻和阻抗的累加吗？

我们知道，当电路中有电感、电容器件时，电路不再表现出纯电阻特性，而要用阻抗来描述。

阻抗（Impedance）相比于电阻（Resistance）来说，考虑了两方面因素：

1. 输入信号的频率对阻抗的影响；
2. 计算电压U和电流I的相位差异；

纯电感的阻抗称为“感抗”，用符号XL表示；纯电容的阻抗称为“容抗”，用符号XC表示。它们统称为“电抗”（Reactance）。

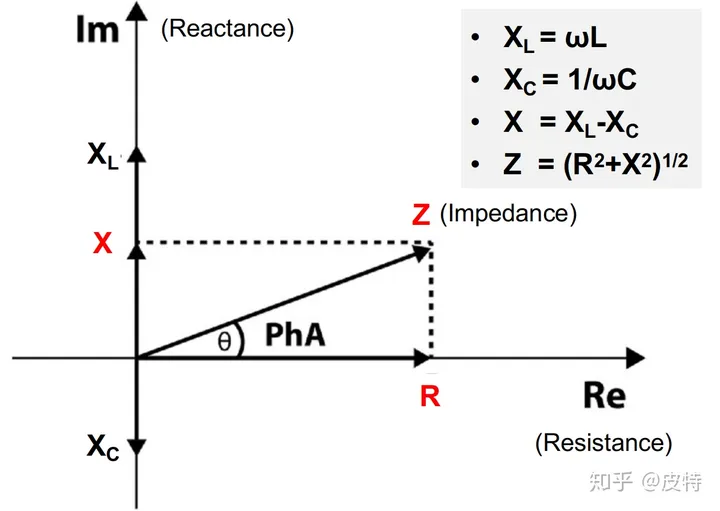
理想情况下，电阻消耗能量；电容、电感不消耗能量，只是转化能量。因为这种本质上的差异，数学上将电阻与电抗（电容/电感）用正交坐标系的二维坐标来表示，横坐标表示电阻，纵坐标表示电抗，特别的，正半轴表示电感感抗，负半轴表示电容容抗：

二维坐标系中，Z（阻抗）可以用复数表示，包含了模|Z|和角度θ两个信息。不过工程上，阻抗常指Z的模——|Z|，上图中已列举了计算公式。

角度θ隐含了电压U和电流I之间的相位信息：

• 如果为正数，表示电压U在相位上领先于电流I；
• 如果为负数，表示电流I在相位上领先于电压U。

这方面如果容易搞混，可以从源头去理解，电感的电流不能突变，先变化的是电压，呈现电感特性（XL>XC）的感性电路亦是如此；电容的电压不能突变，先变化的是电流，呈现电容特性（XC>XL）的容性电路亦是如此。

二、阻抗计算案例

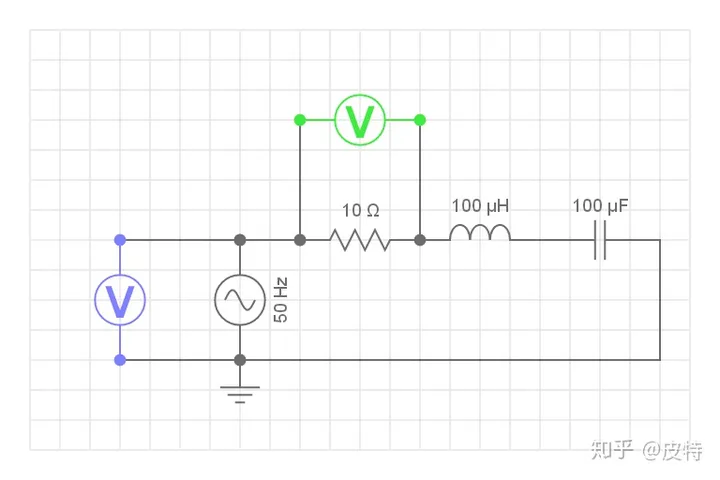
下图中，RLC分别为10Ω、100μH、100μF；输入信号为50Hz，幅度峰值为10V；求电路阻抗、电流有效值？

• XL = 2π*fL = 2*3.14*50*100^10-6 = 0.03Ω
• XC = 1/(2π*fC) = 1/(2*3.14*50*100^10-6) = 31.85Ω
• X = XL-XC = -31.82Ω
• |Z| = (10^2+31.82^2)^(1/2) = 33.35Ω
• Irms = V(s-peak)*0.707/|Z| = 10*0.707/33.35 = 0.212A = 212mA

请注意，通过阻抗算电流或者电压都是基于RMS（有效值）的，所以幅度峰值10V的电源需要乘以0.707算出有效值。

因为是串联电路，所以Irms在所有元器件上一致，我们来分别计算一下电感、电容、电阻上的电压幅度峰值：

• V(L-peak) = V(L-rms) / 0.707 = Irms*XL/0.707 = 0.212*0.03/0.707 = 0.01V
• V(C-peak) = V(C-rms) / 0.707 = Irms*XC/0.707 = 0.212*31.85/0.707 = 9.55V
• V(R-peak) = V(R-rms) / 0.707 = Irms*R/0.707 = 0.212*10/0.707 = 3V

可以看到，RLC三者的电压幅度峰值，如果全部加起来是大于电源电压的幅度峰值10V的，之所以这样，因为RLC各自的电压在相位上有差异，在某个具体的时间点(t)上此消彼长，所以加起来不会大于电源电压的幅度峰值10V。

我们来看下仿真波形，体会一下各个元器件上电压的此消彼长：

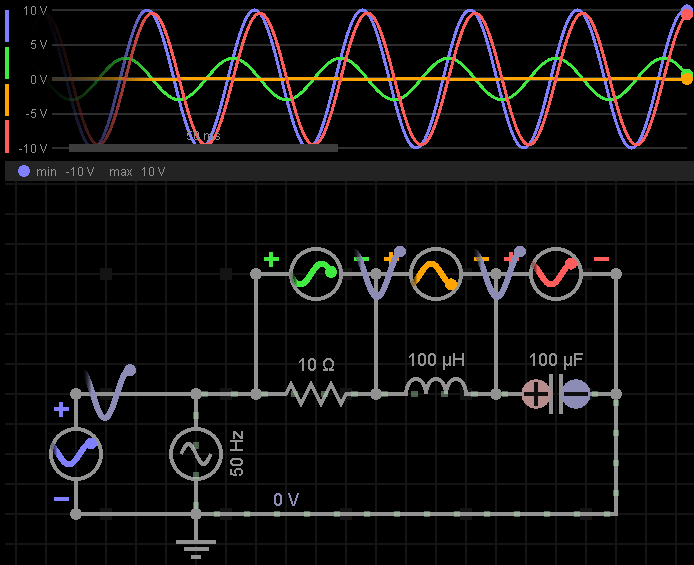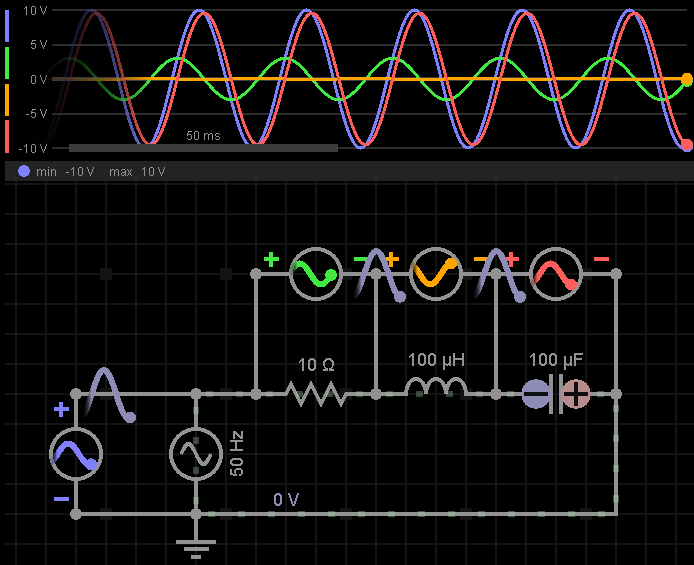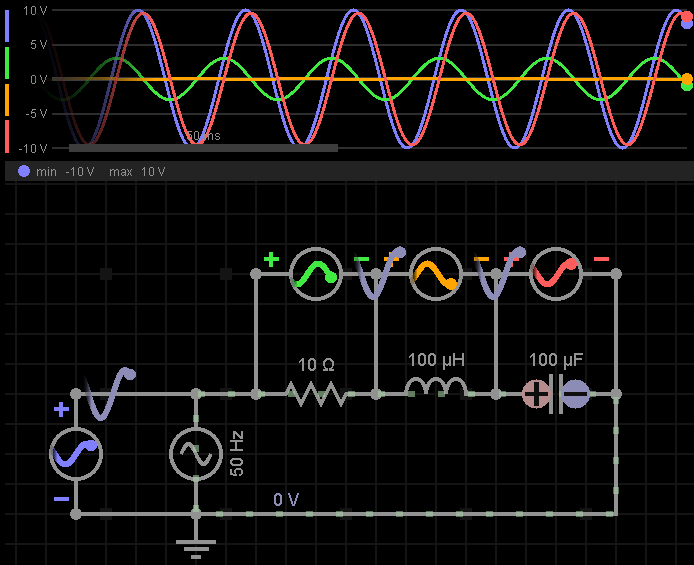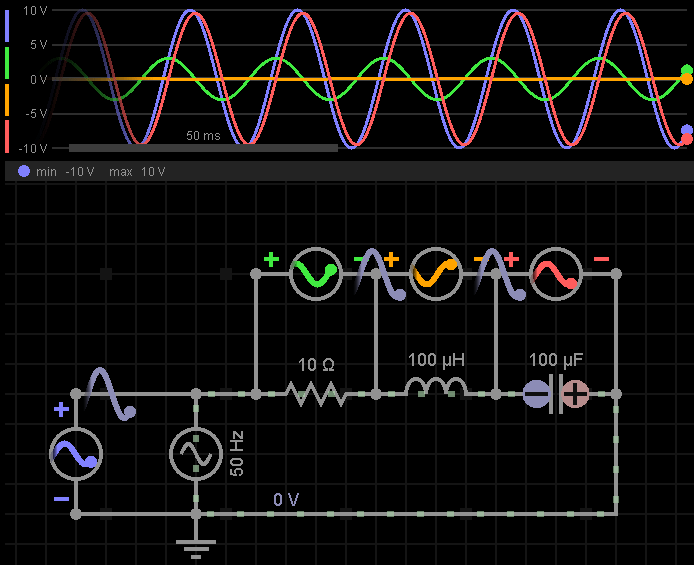
三、当输入信号为谐振频率时会发生什么？

通过前文讲解，看到在计算电路阻抗的时候，会先求出XL（感抗）与XC（容抗）之差，得到电路的X（电抗）大小。

如果XL（感抗）=XC（容抗），那么电路的X（电抗）为0。要到达此目的意味着2π*fL = 1/(2π*fC)，求得f = 1/(2π*(LC)^1/2)：

这个频率称为“谐振频率”（Resonance frequency），是由电路中的L和C决定的。

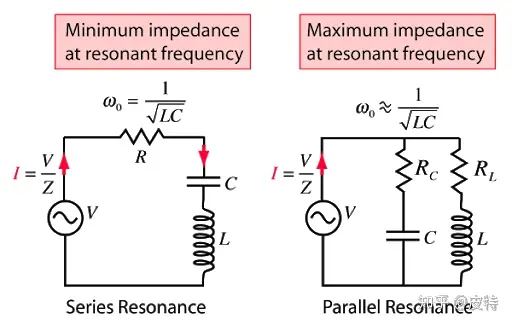
当输入信号的频率与谐振频率一致时，电路的阻抗表现出纯电阻特性，而且|Z|最小。L、C两个元器件的组合对该频率的输入信号而言相当于是短路的。

回到图4中的案例，我们可以计算得到谐振频率约为1.592KHz，将其作为电源频率，看到仿真波形如下：

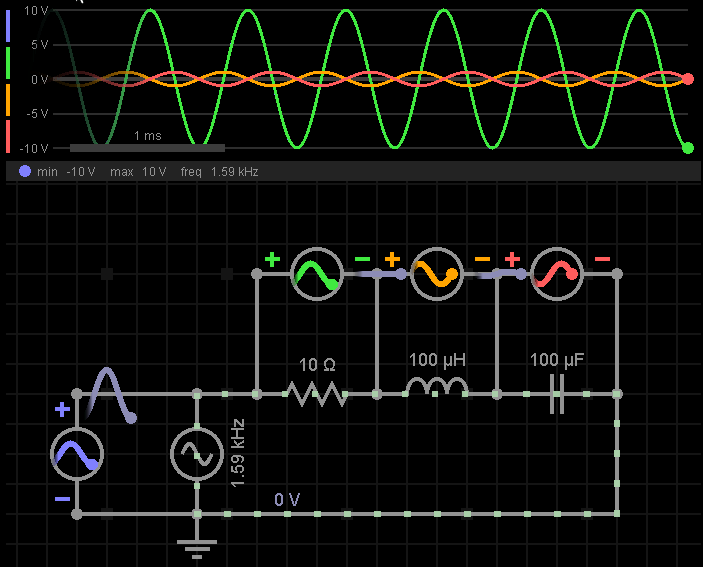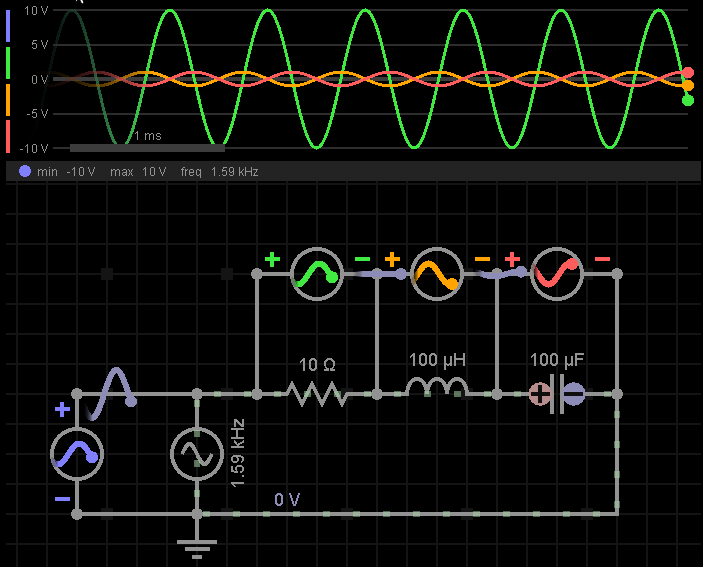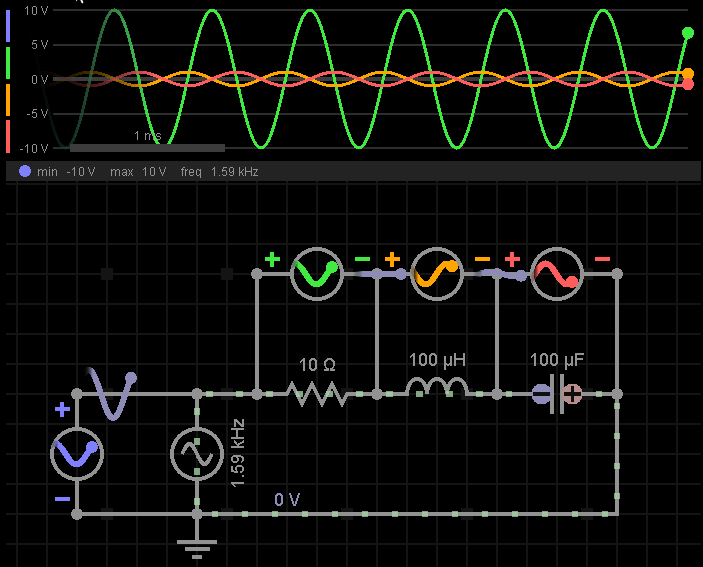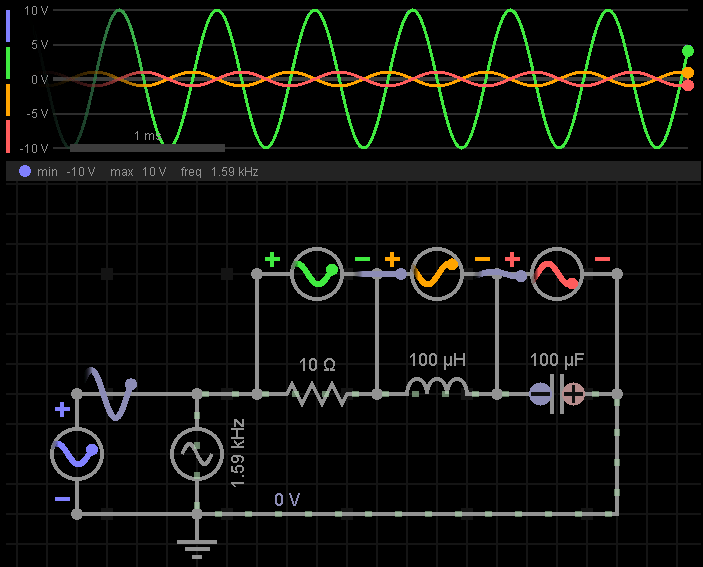
可以看到L、C上电压极性相互，相互抵消，所以L、C的组合相当于是短路的。对比一下图5，在谐振频率的情况下，电阻上获得了最大电压。

当然这是RLC作为串联电路的情况，当RLC作为并联电路时，以谐振频率作为输入，会发生什么呢？下面先给出结论，你可以想一下为什么。

（全文完）