圆曲线
单圆曲线简称圆曲线,是最简单的一种圆曲线,其测设和资料计算都比较容易。但在测设之前,必须进行曲线要素及主要点的里程计算.
圆曲线要素及其计算
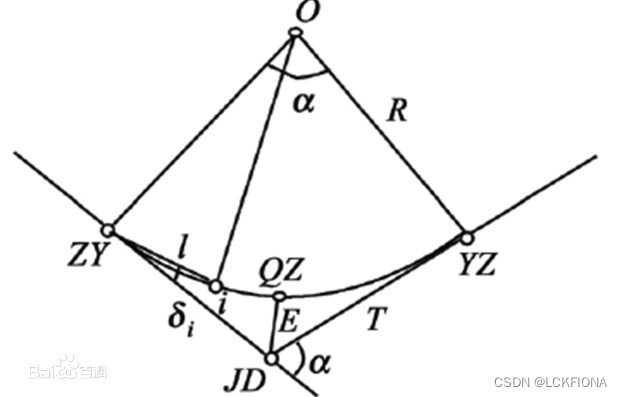
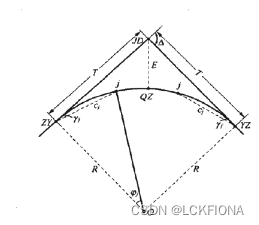
如图所示,圆曲线的半径R、偏角(即线路转向角)α、切线长T、曲线长L、外矢距E及切曲差q(又叫矫正数或超距),称为曲线要素。其中,R以及α均为已知数据。R是在设计中按路线等级及地形条件等因素选定的,α是线路定测时测出的。其余要素可按照下列关系式计算得出
{ T = R t a n ( α / 2 ) L = π / 180 ° ∗ α R E = R ( s e c ( α / 2 ) − 1 ) q = 2 T − L \begin{cases} T=Rtan(α/2)\\ L=π/180°*αR\\ E=R(sec(α/2)-1)\\ q=2T-L \end{cases} ⎩
⎨
⎧T=Rtan(α/2)L=π/180°∗αRE=R(sec(α/2)−1)q=2T−L
圆曲线主要点里程的计算
圆曲线的主要点包括
——ZY点(直圆点),直线与圆曲线的连接点
——QZ(曲中点),圆曲线的中点
——YZ(圆直点),圆曲线与直线的连接点
其主要点的里程,可以通过交点JD的里程计算得出
算例如下
例1,已知α=10°25′10″,R=800m,JD里程为DK11+295.78,求曲线主点要素和主点里程。
T=Rtan(α/2)=72.94m
L=π/180°*αR=145.48m
E=R(sec(α/2)-1)=3.32m
q=2T-L=0.40m
主点里程计算如下
JD DK11+295.78 检核:
-T 72.94 JD DK11+295.78
————————— +L/2 72.94
ZY DK11+222.84 DK11+368.72
+L/2 72.94 ————————
————————— -q 0.40
QZ DK11+295.58 ————————
+L/2 72.94 YZ DK11+368.32
—————————
YZ DK11+368.32
细部点计算(偏角法)
用偏角法测设圆曲线上的细部点是以曲线起点(或终点)作为测站,计算出测站至曲线上任一细部点Pi的弦线与切线的夹角—弦切角i(称为偏角)和弦长Ci或相邻细部点的弦长c,据此确定Pi点的位置。曲线上的细部点即曲线上的里程桩,一般按曲线半径R规定弧长为l的整桩。l一般规定为5m、10m和20m,R越小,l也越小。
由直圆点(圆直点),圆心和细部点三点构成的一个等腰三角形,大圆心角即为α(通过几何关系可以得出和转角α是相等的),细部点到直圆点(圆直点)之间的弧长设为Li,其弧长所对应的弦长设为Ci,弧长所对应的圆心角设为αi,三角形的两个底角设为∠b,则∠b=(180°-αi)/2,偏角i=90°-∠b,即i=αi/2,Li=αi * R(注意这个公式中,αi是弧度制,一般题目中会给度分秒的60进制角度,编程中会给出dd.mmsssss的60进制角度形式,注意要将其化成弧度运算,或者是用Li=αi*R * Π/180°(这里的α是十进制角度)进行运算)。弦长Ci=2R * sini。现将公式总结如下
{ i = α i / 2 C i = 2 R ∗ s i n i L i = α i ∗ R ∗ Π / 180 ° \begin{cases} i=αi/2\\ Ci=2R * sini\\ Li=αi*R * Π/180° \end{cases} ⎩
⎨
⎧i=αi/2Ci=2R∗siniLi=αi∗R∗Π/180°
在进行实地放样时,假设已经测设出主点的位置,右转线路具体测设细部点的方式如下:
正拨
1.安置经纬仪(或全站仪)于曲线起点(ZY)上,瞄准交点(JD),使水平度盘读数设置为00°00′00″ ;
2.水平转动照准部,正拨使度盘读数为i1,沿此方向测设弦长Ci1,定出 P1点;
3.再水平转动照准部,使度盘读数为i2,沿此方向测设长弦Ci2,定出P2点;以此类推,测设其他细部点;
反拨
1.安置经纬仪(或全站仪)于曲线终点(YZ)上,瞄准交点(JD),使水平度盘读数设置为00°00′00″ ;
2.水平转动照准部,反拨使度盘读数为i1,沿此方向测设弦长Ci1,定出 P1点;
3.再水平转动照准部,使度盘读数为i2,沿此方向测设长弦Ci2,定出P2点;以此类推,测设其他细部点;
正拨反拨判断以及左转右转的具体解释
1.左转和右转的判断:沿着路线的方向看,右偏就是右转,有右转角,左偏就是左转,有左转角,这个很好判断,注意跟测量学中的左角右角区别开。
2.正拨反拨:正拨为顺时针转,角度值与度盘读数值增加方向一致;反拨为逆时针转,角度值与度盘读数值减少方向一致(在测试细部点时,左转的情况下,全站仪或经纬仪,架设在ZY点要反拨,架设在YZ点要正拨;右转的情况下,全站仪或经纬仪,架设在ZY点要正拨,架设在YZ点要反拨)
C#代码实现
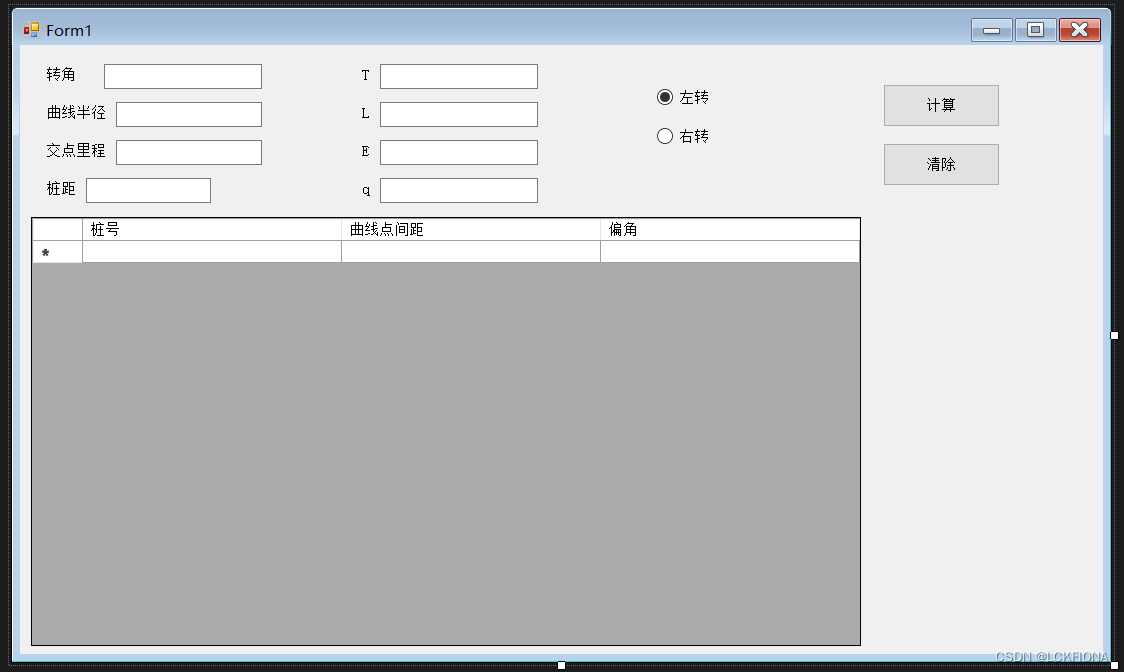
界面设计
控件用了label、textbox、radiobutton、button和datagridview
代码实现
1.先做了一个角度转弧度(JDZHD)和弧度转角度的封装,便于在给定初始的转角α值时,先进行弧度转化,便于Math函数的识别,最后在计算出偏角i的时候,将算出的弧度其转化为角度(实际测设的时候,肯定是拨角度分秒,不可能让你拨一个弧度制的角吧,毕竟仪器是60进制角度制的)
2.计算出T,L,E,q,算出主点的里程,然后注意用IndexOf和Substring进行字符串的截取,把”DK”、“+”、“里程的数值”截取出来
3.在计算桩的个数和桩号的时候,用到了ceiling(向上取整)和floor(向下取整)函数,注意算法问题,我这里以桩距20为例,桩的总个数就是(曲中点里程/20向下取整-直圆点里程/20向上取整)+(圆直点里程/20向下取整-曲中点里程/20向上取整),ZY-QZ和QZ-YZ的桩的个数,就是上式中”+”的前一部分和后一部分
4.在进行for循环时候,特别注意循环的次数,你第0行是要写ZY数据的,然后在写ZY-QZ这个区间里桩的数据,然后写两个QZ点数据,然后再写QZ-YZ这个区间里的桩的数据,然后写YZ的数据。
5.本程序比较简单,只能算不递增公里数的桩号里程,比如说ZY点里程DK1+20.12,YZ点里程DK1+891.22,这就是都在1-2公里之间,你的桩号就都是DK1开头,但如果ZY是DK1+20.12,YZ是DK2+60.11,这就会涉及到DK1和DK2开头的桩号,也就是满一公里之后,DK后面的整公里数值要递增1的问题。
public double JDZHD(double degrees)
{
double d = Math.Truncate(degrees);
double m = Math.Truncate((degrees - d) * 100);
double s = ((degrees - d) * 100 - m) * 100;
double radians = (d + m / 60 + s / 3600) / 180 * Math.PI;
return radians;
}
public static double HTOD(double radians)
{
double dd = radians / Math.PI * 180;
double d = Math.Truncate(dd);
double m = Math.Truncate((dd - d) * 60);
double s = Math.Round(((dd - d) * 60 - m) * 60, 4);
double degrees = d + m / 100 + s / 10000;
return degrees;
}
private void button1_Click(object sender, EventArgs e)
{
double ZJ = double.Parse(textBox1.Text);//转角
double R = double.Parse(textBox2.Text);//半径
double d = double.Parse(textBox4.Text);//桩距
double ZJ1 = JDZHD(ZJ);
double T = R * Math.Tan(ZJ1 / 2);
double L = R*ZJ1;
double E = R * (1 / Math.Cos(ZJ1 / 2) - 1);
double q = 2 * T - L;
textBox5.Text = T.ToString();
textBox6.Text = L.ToString();
textBox7.Text = E.ToString();
textBox8.Text = q.ToString();
string s = textBox3.Text;
string s1 = s.Trim();
int f1 = s1.IndexOf('K');
int f2 = s1.IndexOf('+');
string s2 = s1.Substring(0, f1 + 1); //DK
string s3 = s1.Substring(2, f2 - f1 - 1);
string s4 = s1.Substring(f2);
double LC = double.Parse(s3) * 1000 + double.Parse(s4);
int s5 = Convert.ToInt32(s3);
double JD = LC;
double ZY = JD - s5 * 1000 - T;
double YZ = ZY + L;
double QZ = ZY + (L / 2);
int A = (int)Math.Ceiling(ZY / d);
int B = (int)Math.Floor(YZ / d);
int Q1 = (int)Math.Floor(QZ / d);
int Q2 = (int)Math.Ceiling(QZ / d);
int n1 = Q1 - A;
int n2 = B - Q2;
double[,] mm = new double[n1 + 3, 3];
mm[0, 0] = ZY;
mm[0, 1] = 0;
mm[0, 2] = 0;
mm[1, 0] = A * d;
mm[n1 + 1, 0] = B * d;
mm[n1 + 2, 0] = QZ;
mm[n1 + 2, 1] = QZ - Q1 * d;
mm[n1 + 2, 2] = HTOD(2 * Math.PI - ((QZ - ZY) / R / 2));
if (radioButton2.Checked == true)
{
mm[n1 + 2, 2] = HTOD((QZ - ZY) / R / 2);
}
dataGridView1.Rows.Add();
dataGridView1.Rows[0].Cells[0].Value = s2 + s3 + "+" + mm[0, 0];
dataGridView1.Rows[0].Cells[1].Value = mm[0, 1];
dataGridView1.Rows[0].Cells[2].Value = mm[0, 2];
for (int i = 0; i < n1 + 1; i++)
{
mm[i + 1, 0] = A * d + d * i;//里程
mm[i + 1, 1] = mm[i + 1, 0] - mm[i, 0];//曲线点间距
mm[i + 1, 2] = HTOD(2 * Math.PI - ((mm[i + 1, 0] - mm[0, 0]) / R / 2));//偏角
if (radioButton2.Checked == true)
{
mm[i + 1, 2] = HTOD((mm[i + 1, 0] - mm[0, 0]) / R / 2);
}
dataGridView1.Rows.Add();
dataGridView1.Rows[i + 1].Cells[0].Value = s2 + s3 + "+" + mm[i + 1, 0];
dataGridView1.Rows[i + 1].Cells[1].Value = Math.Round(mm[i + 1, 1], 4);
dataGridView1.Rows[i + 1].Cells[2].Value = Math.Round(mm[i + 1, 2], 8);
}
dataGridView1.Rows.Add();
dataGridView1.Rows[n1 + 2].Cells[0].Value = s2 + s3 + "+" + mm[n1 + 2, 0];
dataGridView1.Rows[n1 + 2].Cells[1].Value = Math.Round(mm[n1 + 2, 1], 4);
dataGridView1.Rows[n1 + 2].Cells[2].Value = mm[n1 + 2, 2];
double[,] ww = new double[n1 + 3, 3];
ww[0, 0] = QZ;
ww[1, 0] = Q2 * d;
ww[n2 + 1, 0] = B * d;
ww[n2 + 2, 0] = YZ;
ww[n2 + 1, 1] = YZ - B * d;
for (int x = 0; x < n2 + 2; x++)
{
if (x < n2 + 1)
{
ww[x + 1, 0] = Q2 * d + d * x;
ww[x, 1] = ww[x + 1, 0] - ww[x, 0];
}
ww[x, 2] = HTOD((ww[n2 + 2, 0] - ww[x, 0]) / R / 2);
if (radioButton2.Checked == true)
{
ww[x, 2] = HTOD(2 * Math.PI - ((ww[n2 + 2, 0] - ww[x, 0]) / R / 2));
}
dataGridView1.Rows.Add();
dataGridView1.Rows[x + n1 + 3].Cells[0].Value = s2 + s3 + "+" + ww[x, 0];
dataGridView1.Rows[x + n1 + 3].Cells[1].Value = Math.Round(ww[x, 1], 4);
dataGridView1.Rows[x + n1 + 3].Cells[2].Value = Math.Round(ww[x, 2], 8);
}
dataGridView1.Rows.Add();
dataGridView1.Rows[n2 + n1 + 5].Cells[0].Value = s2 + s3 + "+" + ww[n2 + 2, 0];
dataGridView1.Rows[n2 + n1 + 5].Cells[1].Value = ww[n2 + 2, 1];
dataGridView1.Rows[n2 + n1 + 5].Cells[2].Value = ww[n2 + 2, 2];
}
private void button2_Click(object sender, EventArgs e)
{
textBox1.Text = "";
textBox3.Text = "";
textBox2.Text = "";
textBox4.Text = "";
textBox5.Text = "";
textBox6.Text = "";
textBox7.Text = "";
textBox8.Text = "";
dataGridView1.Rows.Clear();
}
今天的文章圆曲线计算实例_圆曲线的五个要素计算例题分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/85429.html