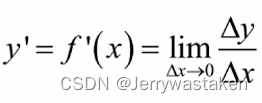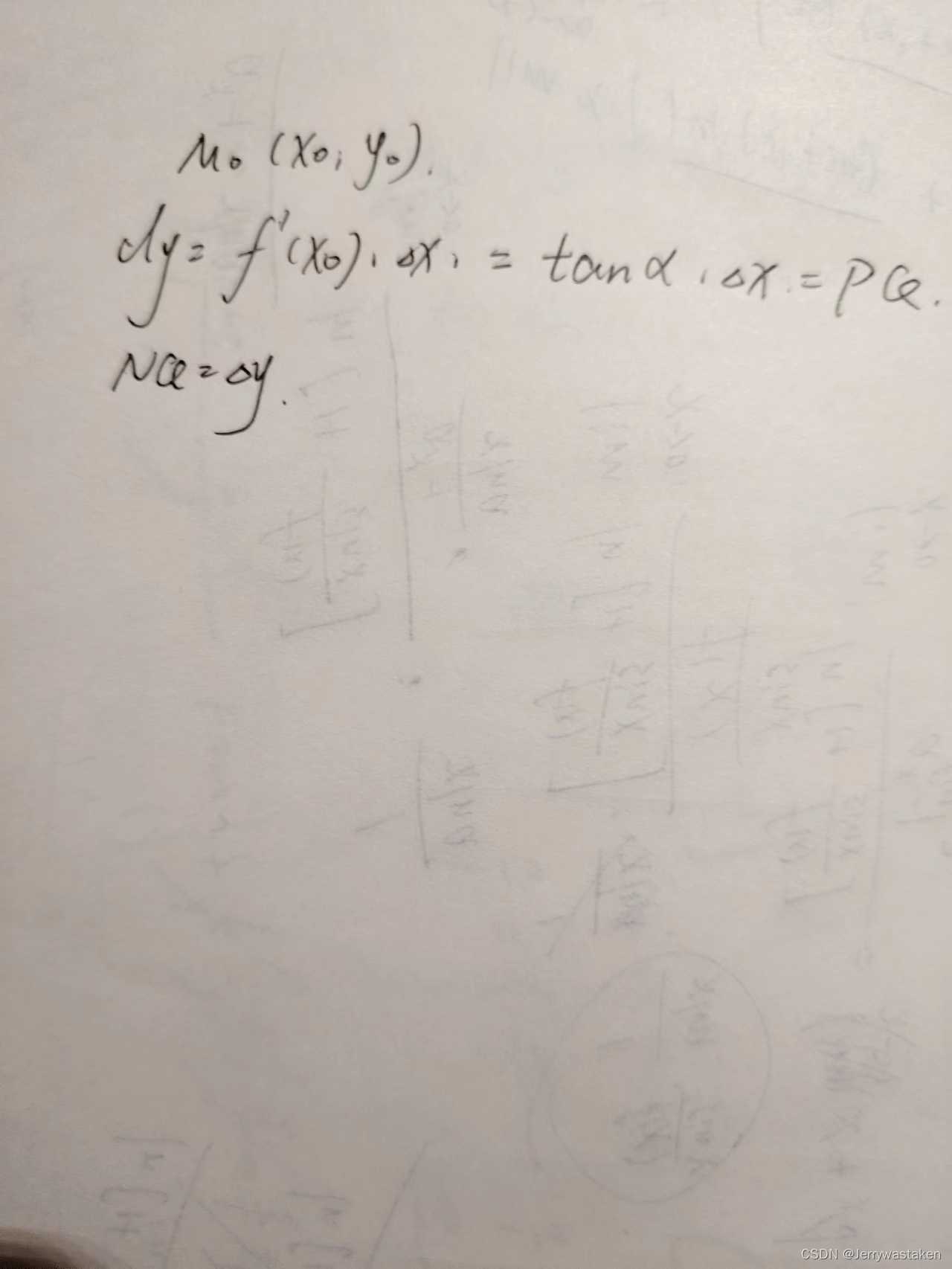什么叫微分?_什么叫做微分「建议收藏」

总所周知，世界是不断变化的，如何使用数学语言具象化这些变化，成了我们值得探讨的问题，其中，微分首当其冲，可以说微分是研究变化量的利器，那我们该如何理解微分呢，什么是微分，我们可以从两个角度，代数和几何的角度去研究它

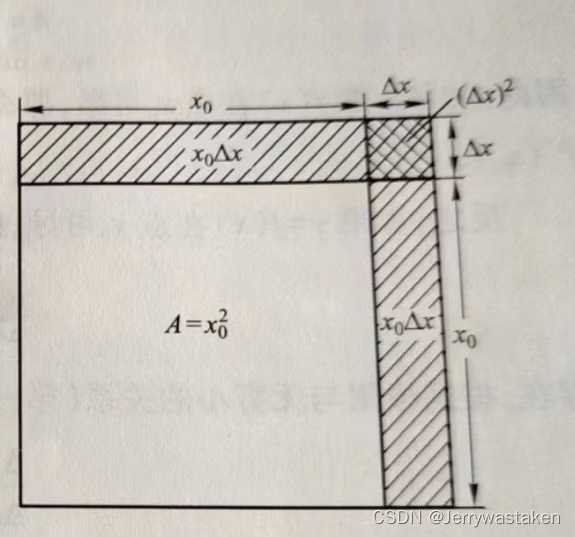
先看一个例子：一块正方形金属薄片受温度变化的影响，其边长由变到+，如图：

我们很容易就可以得出函数相应的增量

通过化简，我们可以得出，=

由上式我们可以看出，被分成了两个部分,一部分是是的线性函数，即图中带有斜线的两个矩形面积的和，而第二部分则是交叉斜线的小正方形的面积，当趋近于0时，第二部分是比高阶的无穷小，。所以如果边长改变很微小，可以近似的用第一部分来代替。此外，我们可以注意到，与并没有关系，所以，我们可以对上面的式子处理一下，改变一下表达方式，为：

其中，A是不依赖于的常数，所以我们可以将A理解为的线性函数

回到函数里，如果函数在x处可导，有

根据函数极限的定理，函数f(x)具有极限的充要条件是 f(x)=A+

所以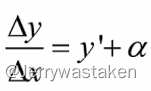，（这里我们将看作f(x))，则有：

所以，我们就可以有微分的概念

二.微分与导数的关系

这里，我们也许有疑问，与dy的关系是什么，有差别还是相等？

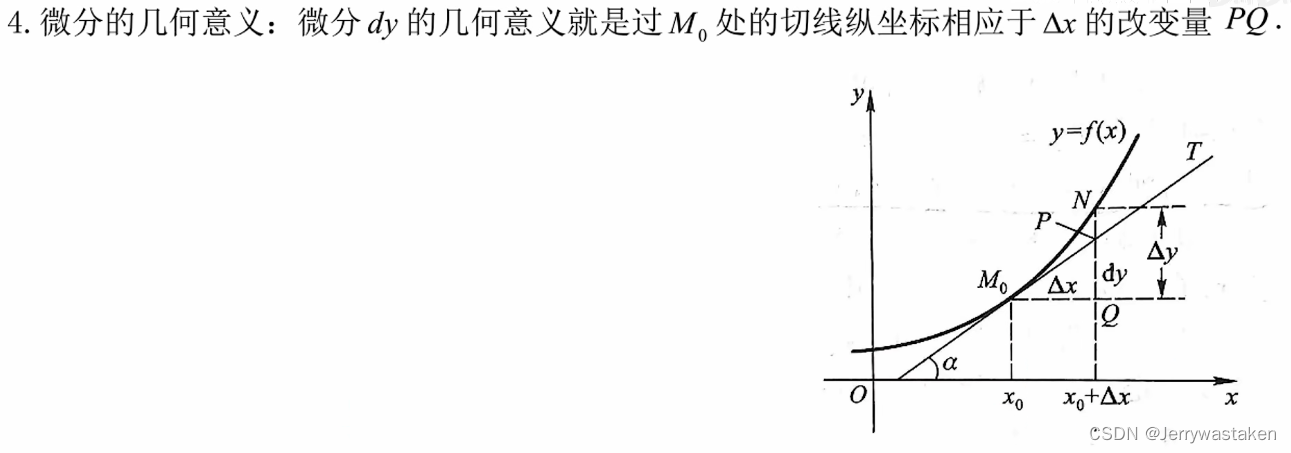
为了证明这个问题，我们可以用微分的几何定义来判断

所以我们可以很主观的看出，两个并不相等

根据微分的定义，与导数一样，我们也可以得到不同函数微分的表格

今天的文章什么叫微分?_什么叫做微分「建议收藏」分享到此就结束了，感谢您的阅读。