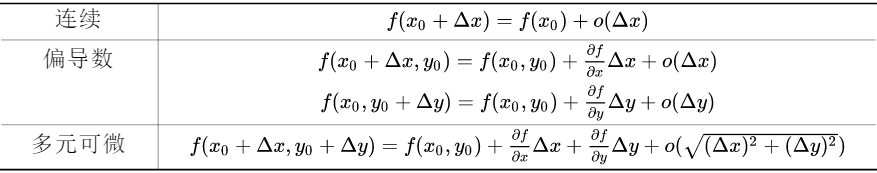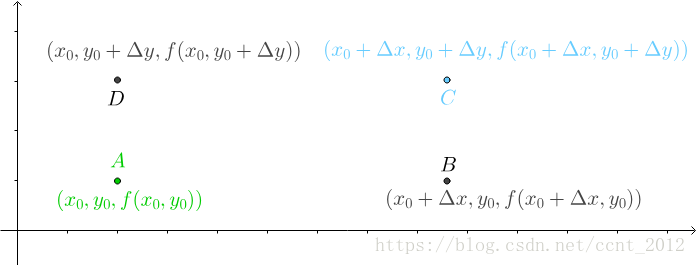偏导数连续,可微,连续之间的关系_偏导连续是可微的什么条件「建议收藏」

1 连续的含义

通俗来说，用笔作画，不提笔画出来的曲线就是连续的：

1.1 没有缝隙

我们对连续的函数曲线的直观感受是没有缝隙：

1.2 另一层含义

2 可微的含义

可微可导的几何意义

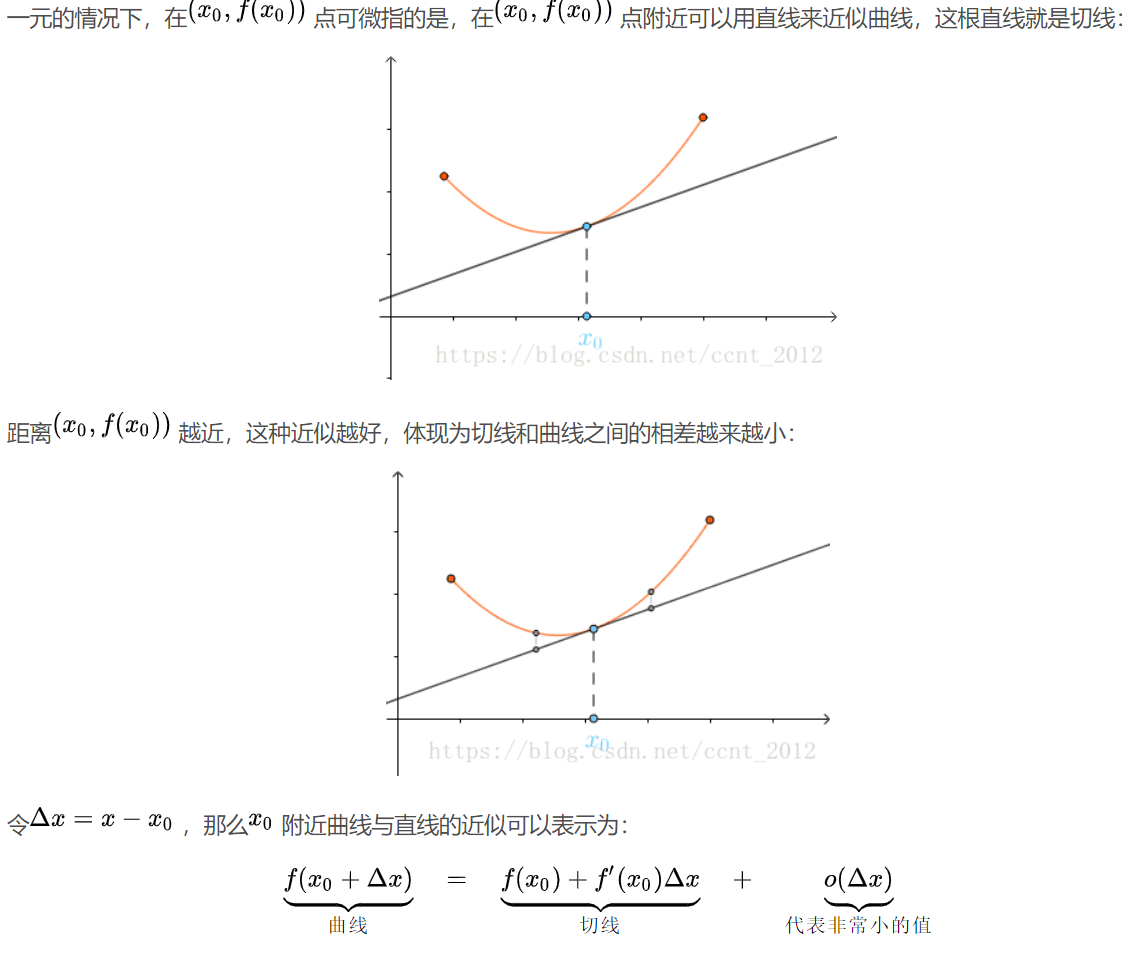
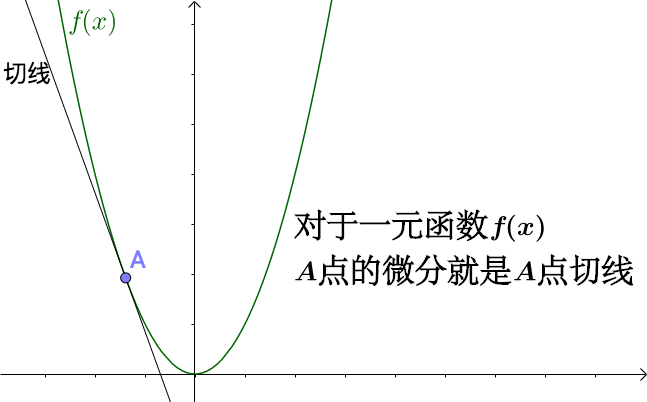
对于一元函数,可微的几何意义是该点处存在切线;对于二元函数,可微表示该点处存在切平面.
一元函数可微与可导等同.在一点可微的几何意义是图形在该点有不与y轴平行的切线.二元函数在一点可微的几何意义是图形曲面在该点有不与z轴平行的切平面.
对于可导的点来说,这一点得到数是切线的斜率,这时的切线就是唯一的一条不穿过曲线但和曲线只有一个交点的直线.

2.1 单变量函数的微分

在一元函数中的微分就是函数的切线

2.2 多变量函数的微分

多元的情况下，就要复杂一些。

2.2.1 偏导数

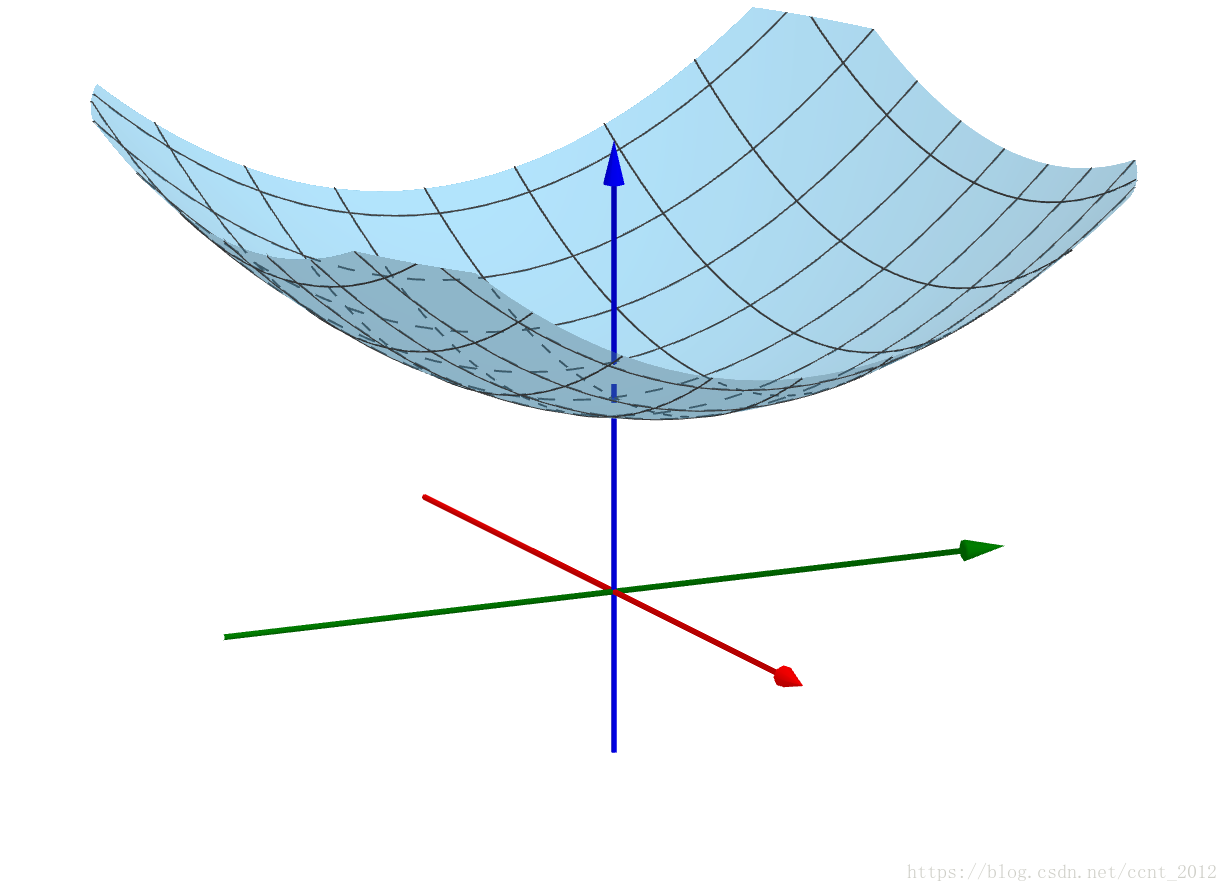
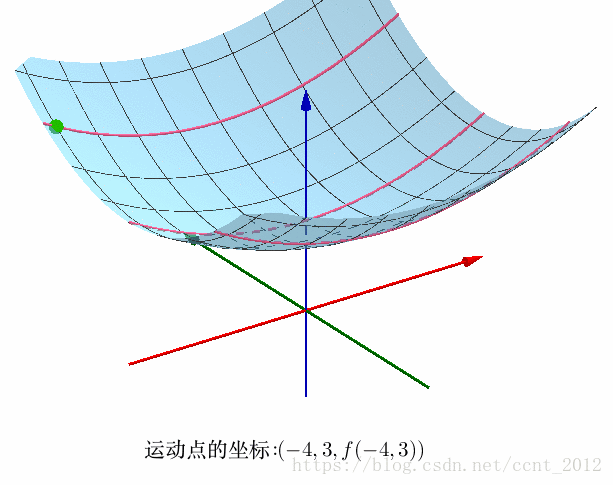
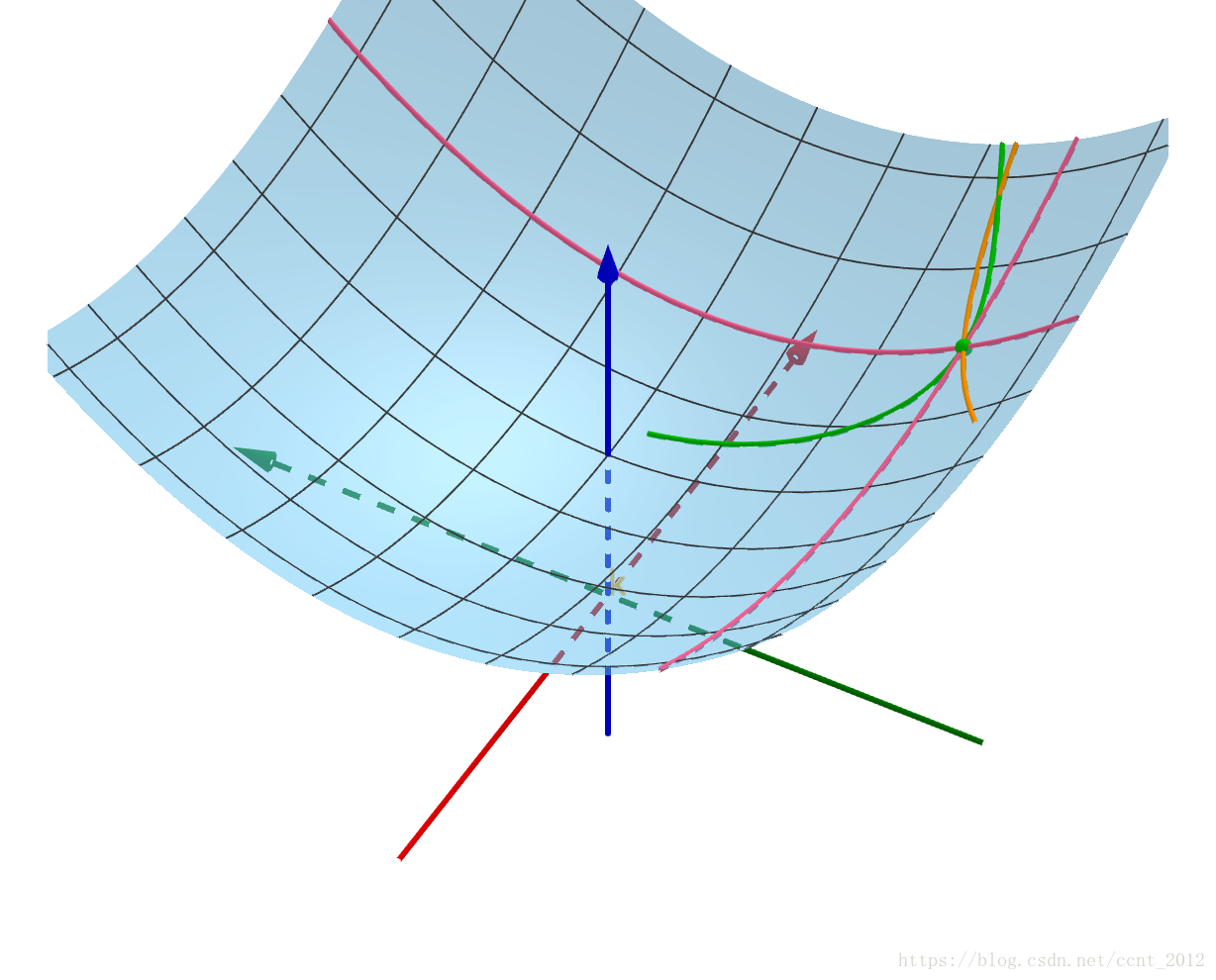
首先要对偏导数有所了解。多变量的函数f(x,y) 可以是三维空间中的曲面

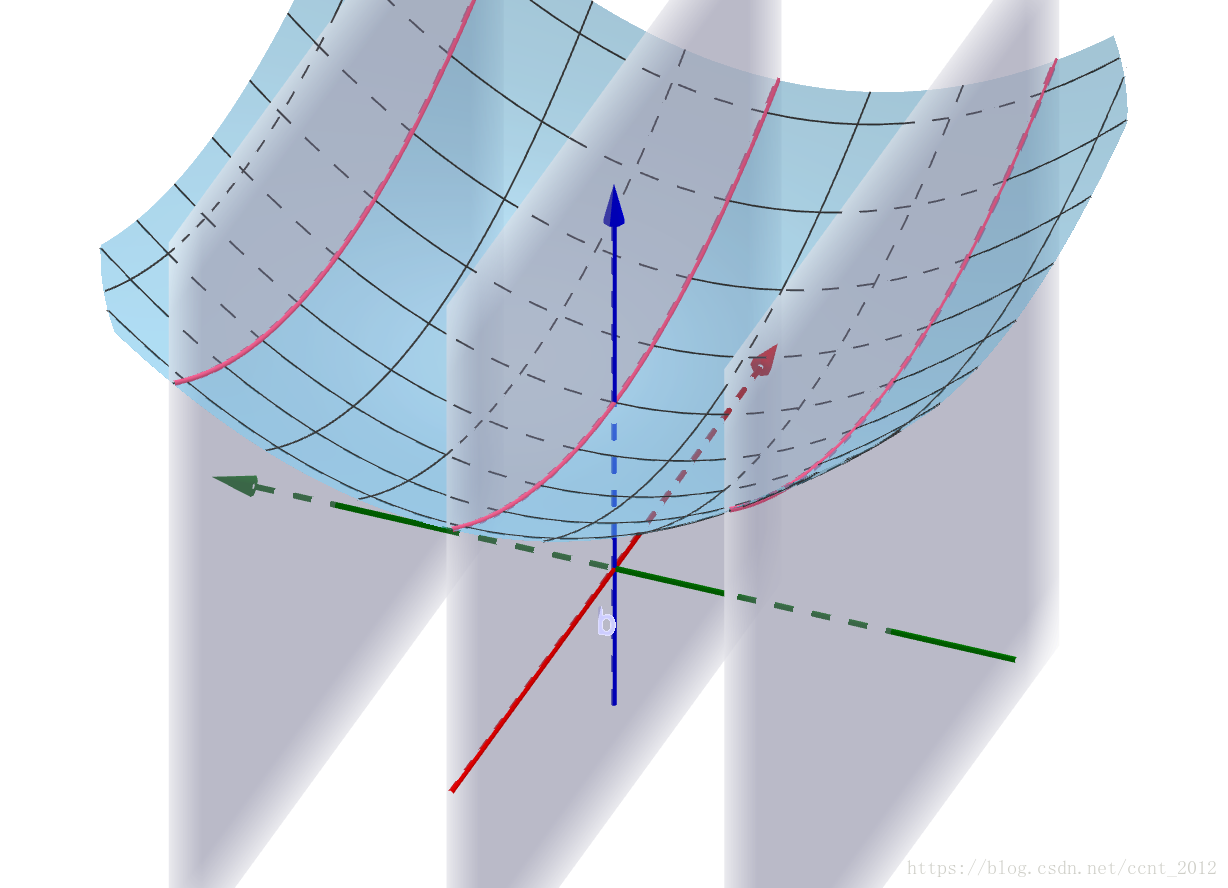
平面y=t,t $\in R$ 是一系列平面，它们与曲面交于一条条曲线：

很显然，点在这些曲线上运动，y 是不会变化的，只有x 会变化：

2.2.2 微分

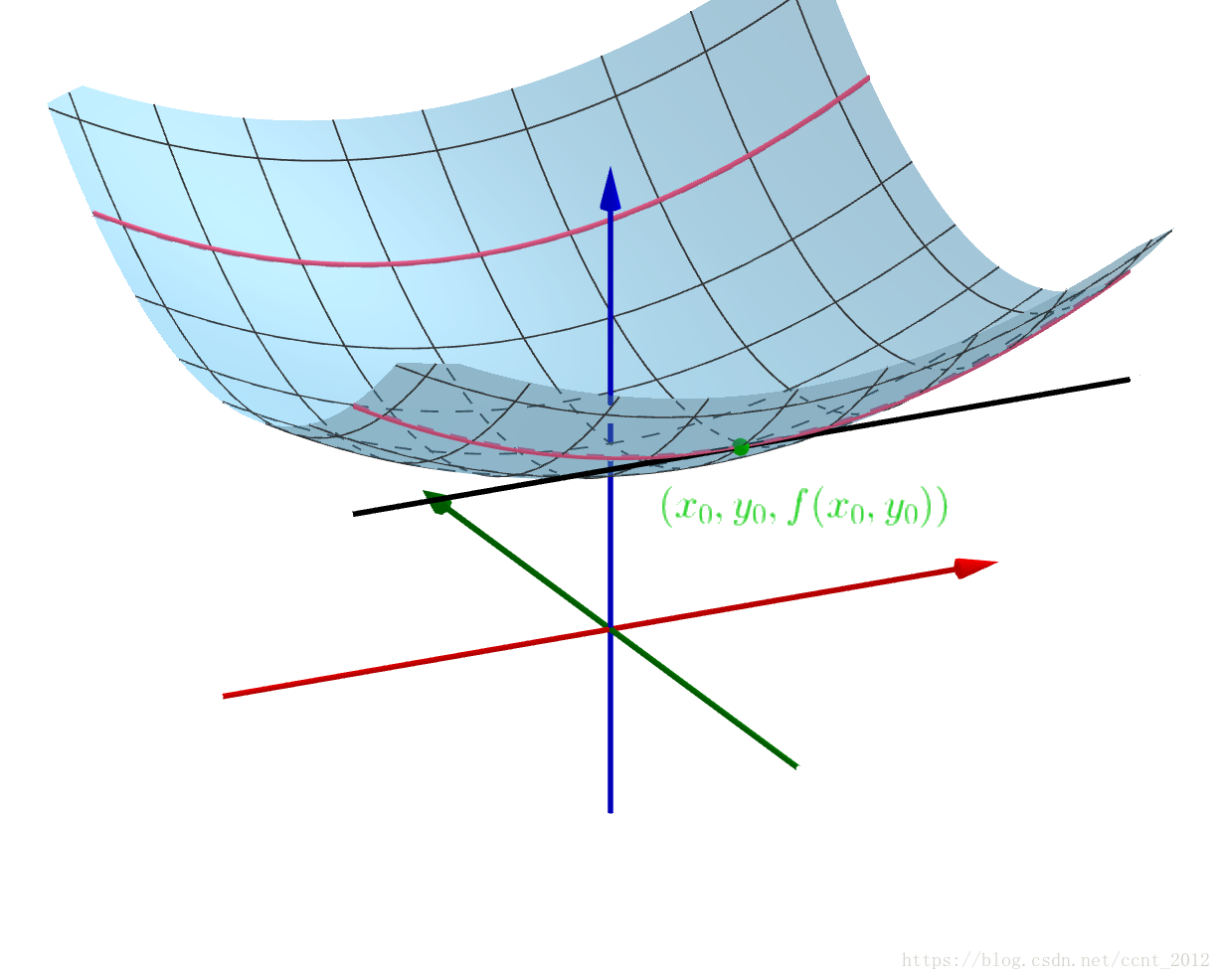
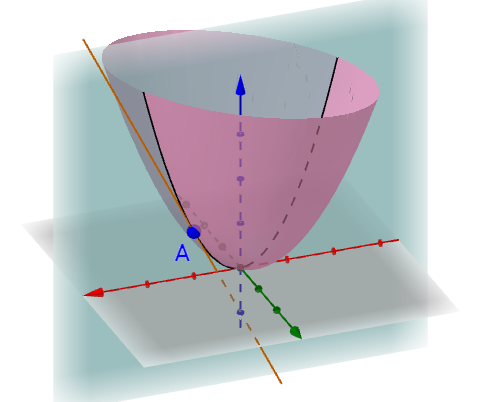
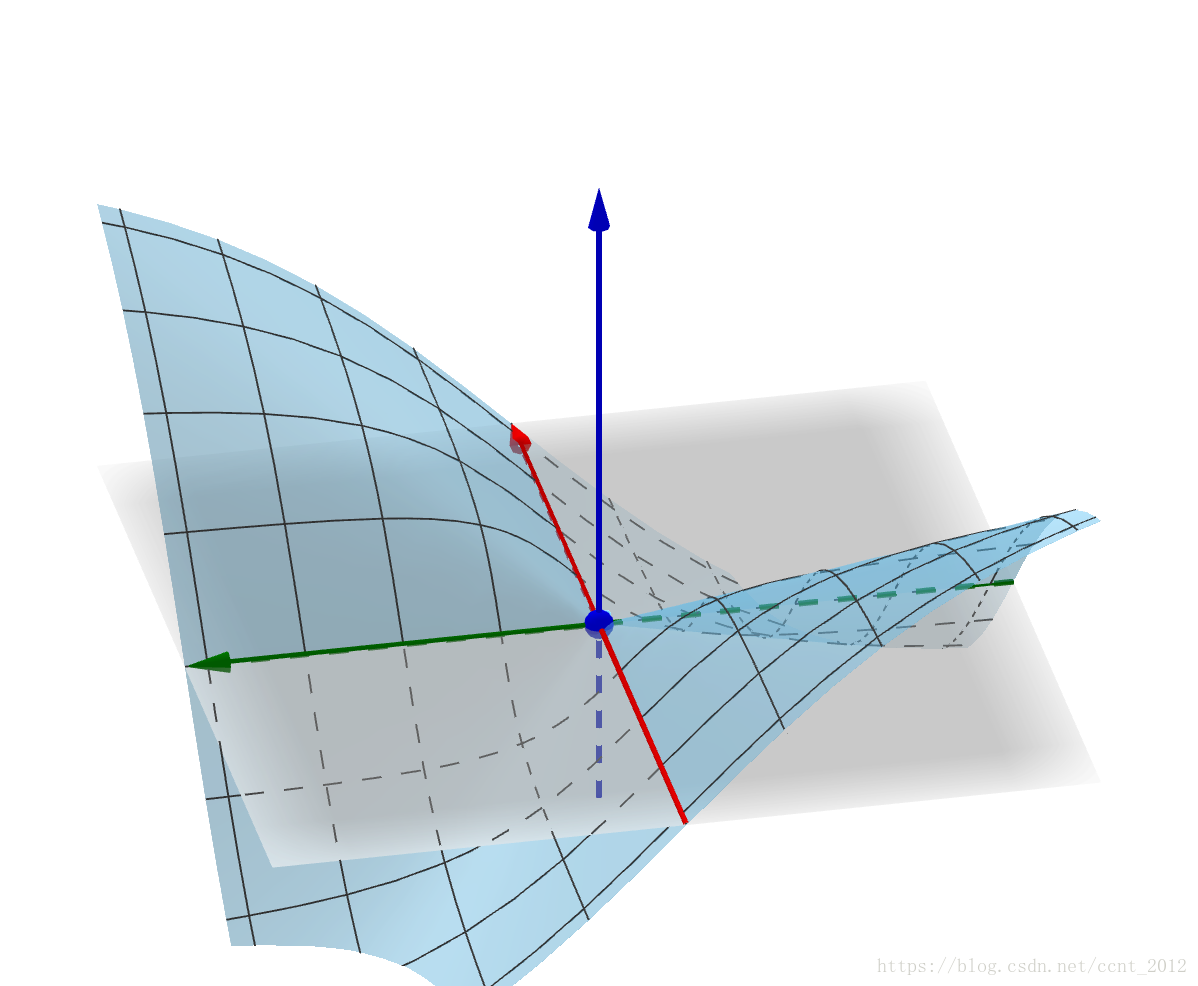
多变量的函数f(x,y) 在 $x_0,y_0,f(x_0,y_0))$ 点的微分，指的是在 $x_0,y_0,f(x_0,y_0))$ 点找到一个平面来近似曲面，这就是切平面：

偏微分

在一元函数中的微分就是函数的切线：

关于微分就是切线，我写的很多文章（比如我最近的如何通俗解释全微分？）都希望大家可以理解这一点，虽然要严格讲清楚需要微分几何、流型的知识，但是我认为掌握了这一点对于我们学习微积分很有帮助。

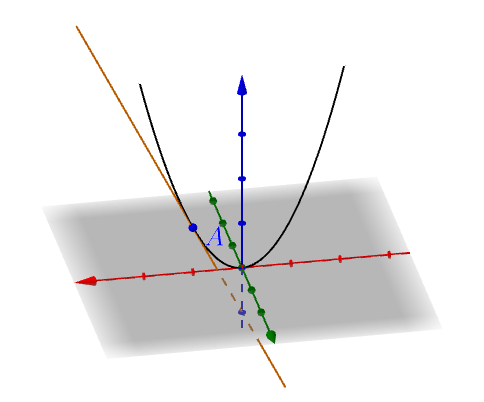
我们发挥一下空间想象力，把它从平面中拽出来，进入三维空间：

之前是平面曲线，现在是空间曲线。切线仍然是切线，微分仍然是微分。

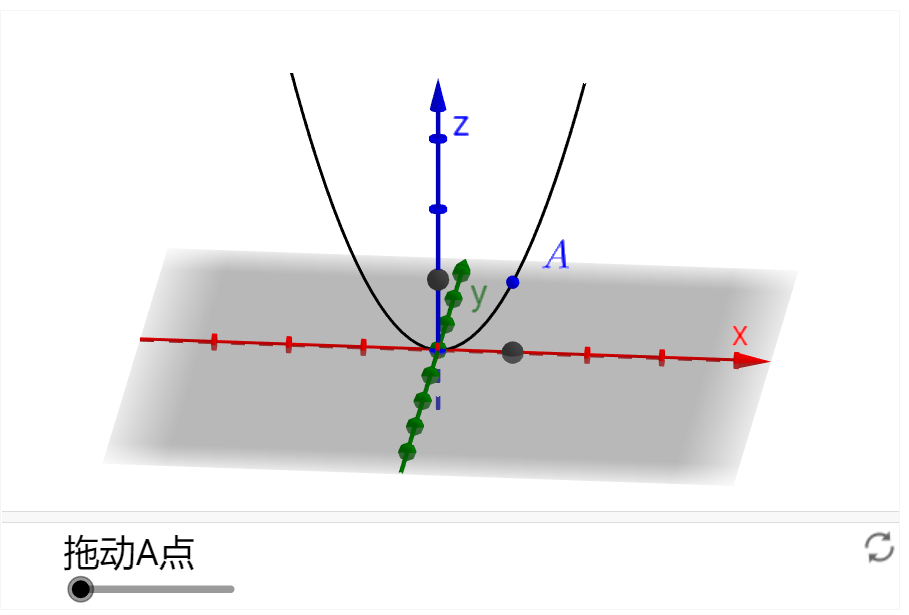
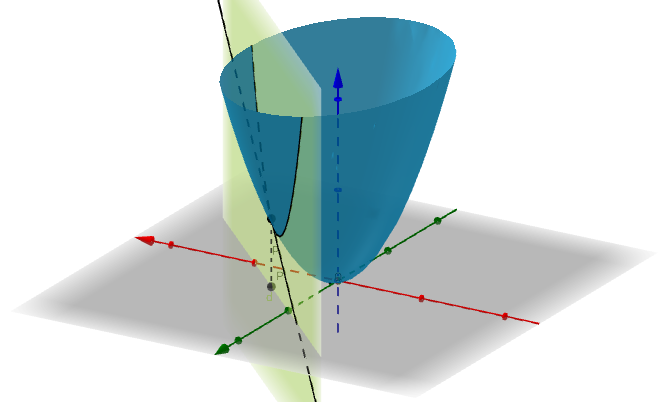
我们再想象一下，其实这个空间曲线是y=0这个空间平面与f(x,y)这个空间曲面的交线：

我们就把这个切线称为f(x,y)对于x的偏微分。为什么是对于x的呢？因为这是y=0与f(x,y)的交线，在这条线上无论点怎么变化，都要满足y=0，即y是常数不会变化。

你来玩玩下面这个互动操作就知道了，点在线上变化只会改变z和x：

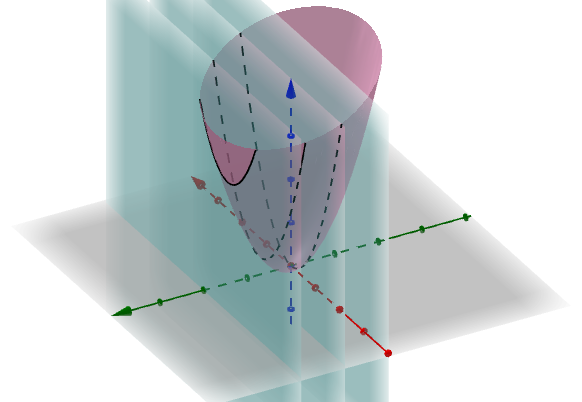
理解了这个，就可以举一反三，所有y=C（C为常数）的平面与f(x,y)的交线都是满足刚才说的特点：

这些交线上的点的切线都是f(x,y)关于x的偏微分。

当然，如果f(x,y)与x=C（C为常数）得到的交线，这些交线的切线就是f(x,y)关于y的偏微分。

总结，偏微分就是：

固定y，变换x得到的就是f(x,y)关于x的偏微分
固定x，变换y得到的就是f(x,y)关于y的偏微分

偏导数

偏微分理解了偏导数就好理解了，就是偏微分的斜率，现在你应该可以明白为什么我们在求f(x,y)对于x的偏导数的时候，我们把y当作常数来看待了吧。

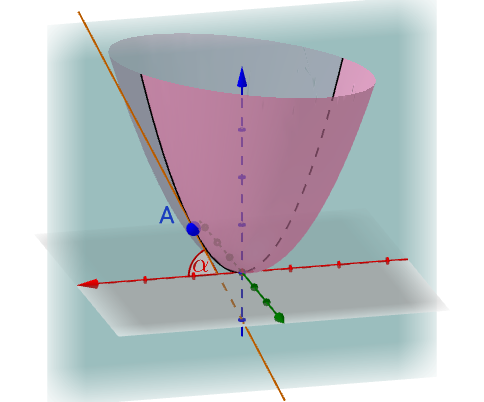
只是有一点需要说明，在三维空间中角度可以有不同的定义，计算斜率的时候我们是看下面这个 $\alpha$ 角：

总结，偏导数就是偏微分的斜率。

2.3 全微分

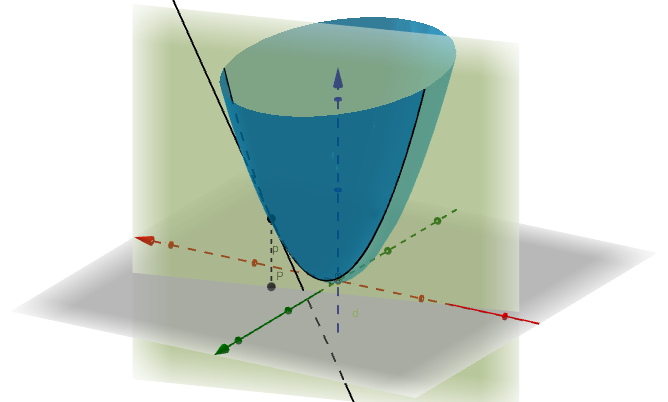
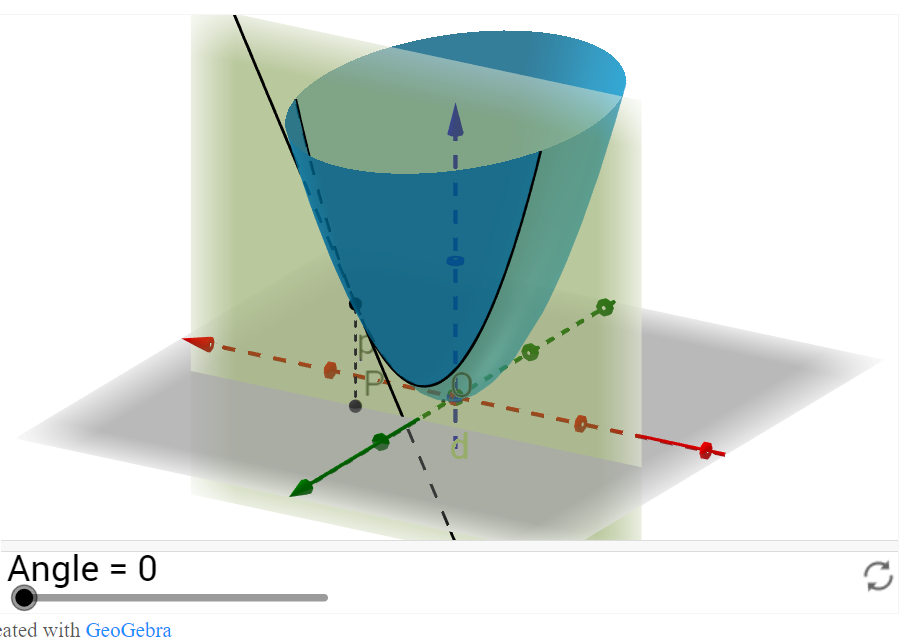
其实，不光是y=C或者x=C这样的平面可以和f(x,y)相交得到交线，所有和xy平面垂直的平面都相交得到交线，这些交线都会有切线（微分）：

这个平面相交得到的交线：

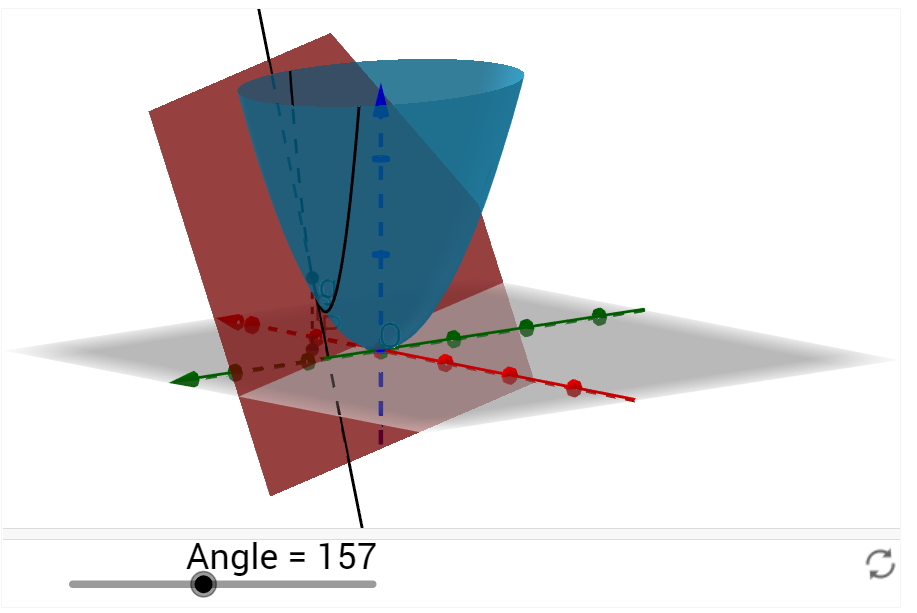
这个平面也可以：

总之，应该是360°无死角，自己动手试试：

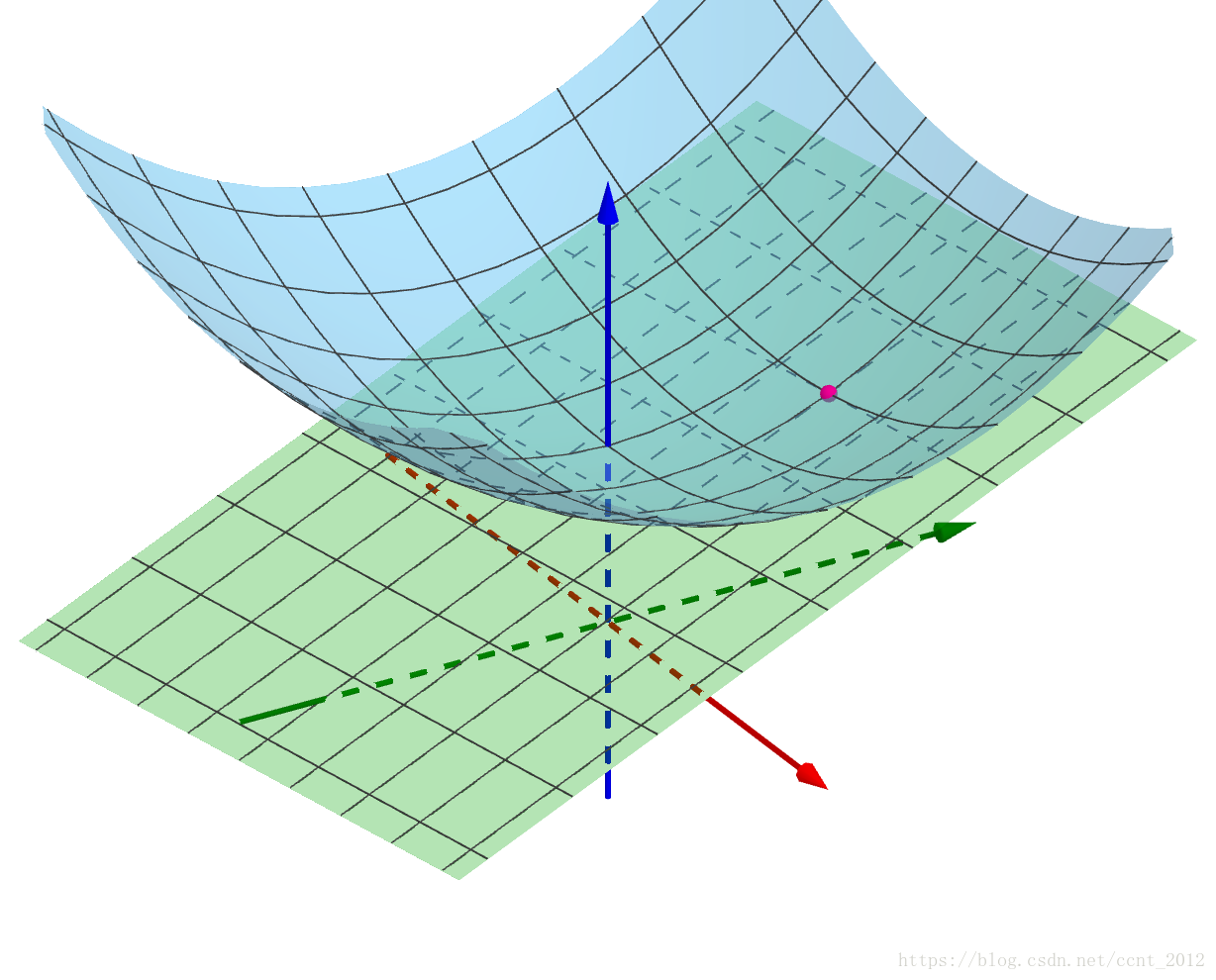
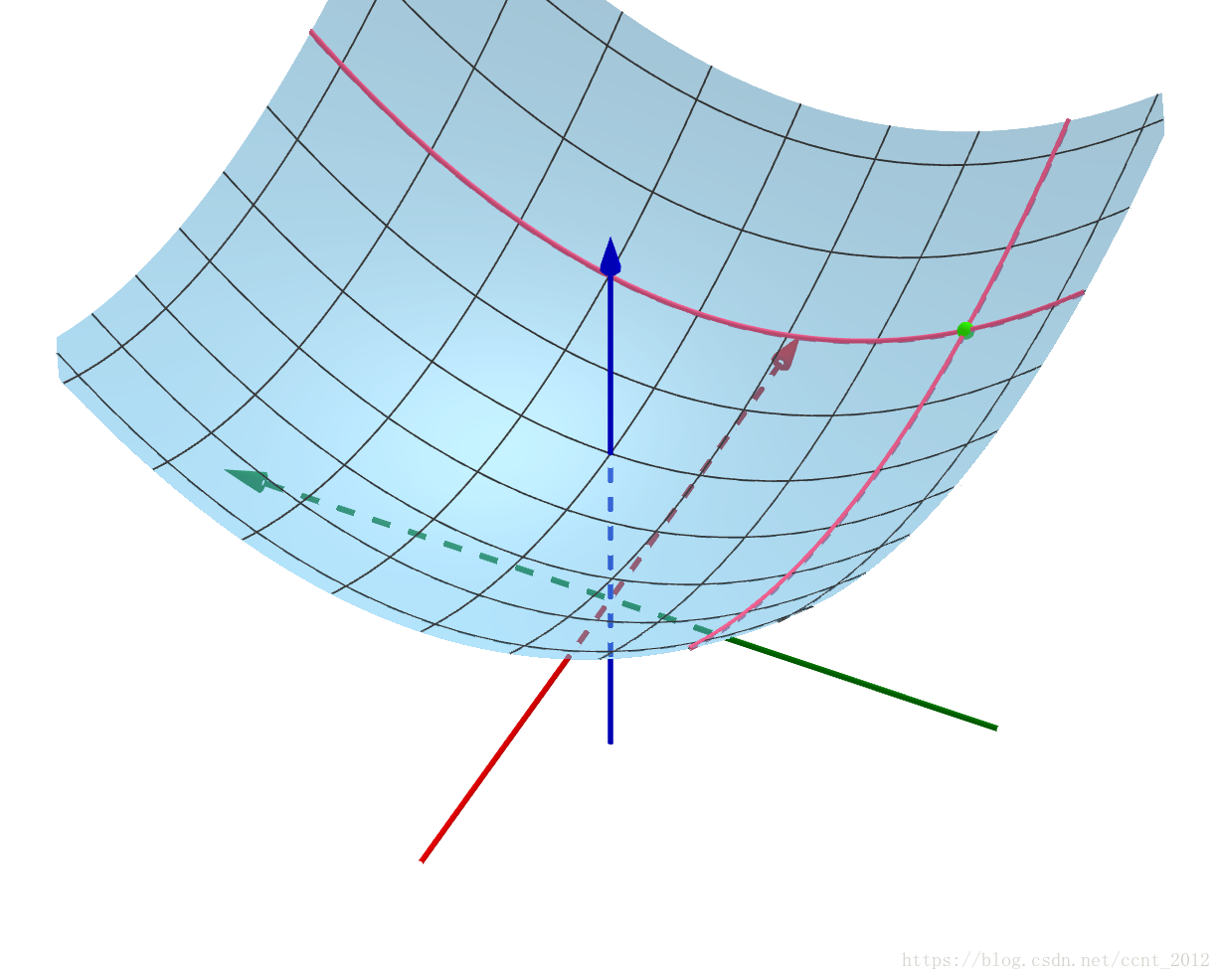
如果这些切线都存在，并且这些切线（无数条）还都在同一个平面上（平面不是曲面），那么得到的这个平面就是全微分（也叫做切平面，或者说切空间）：

总结，全微分就是：
360°微分都存在
并且这些微分要共面，得到的就是全微分

2.3 微分与偏微分的关系

很显然，过(x_0,y_0,f(x_0,y_0)) 点，并不是只有x,y 方向的曲线（两个方向的曲线的切线就是偏微分）

还有无数别的方向的曲线（随便画了两条）：

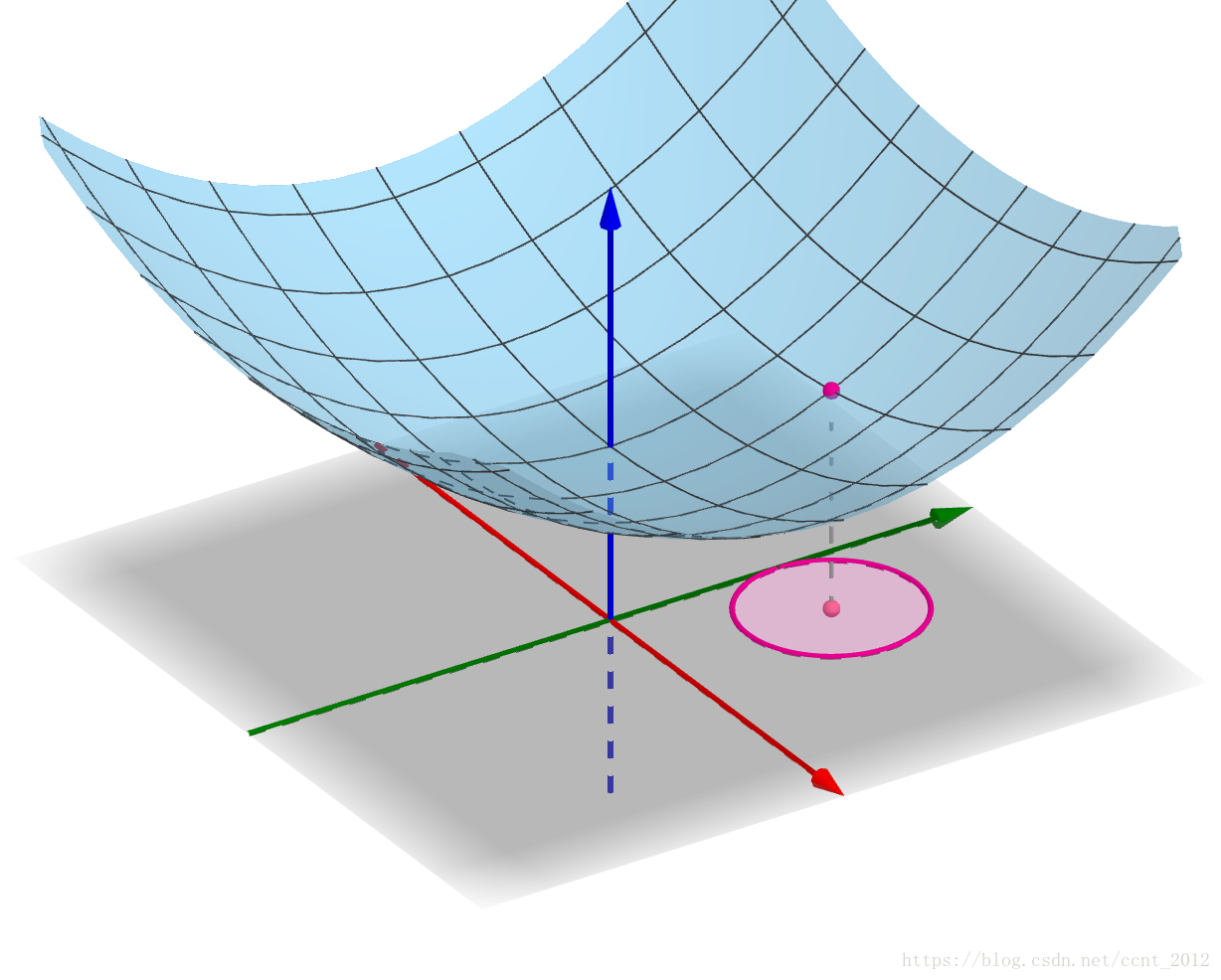
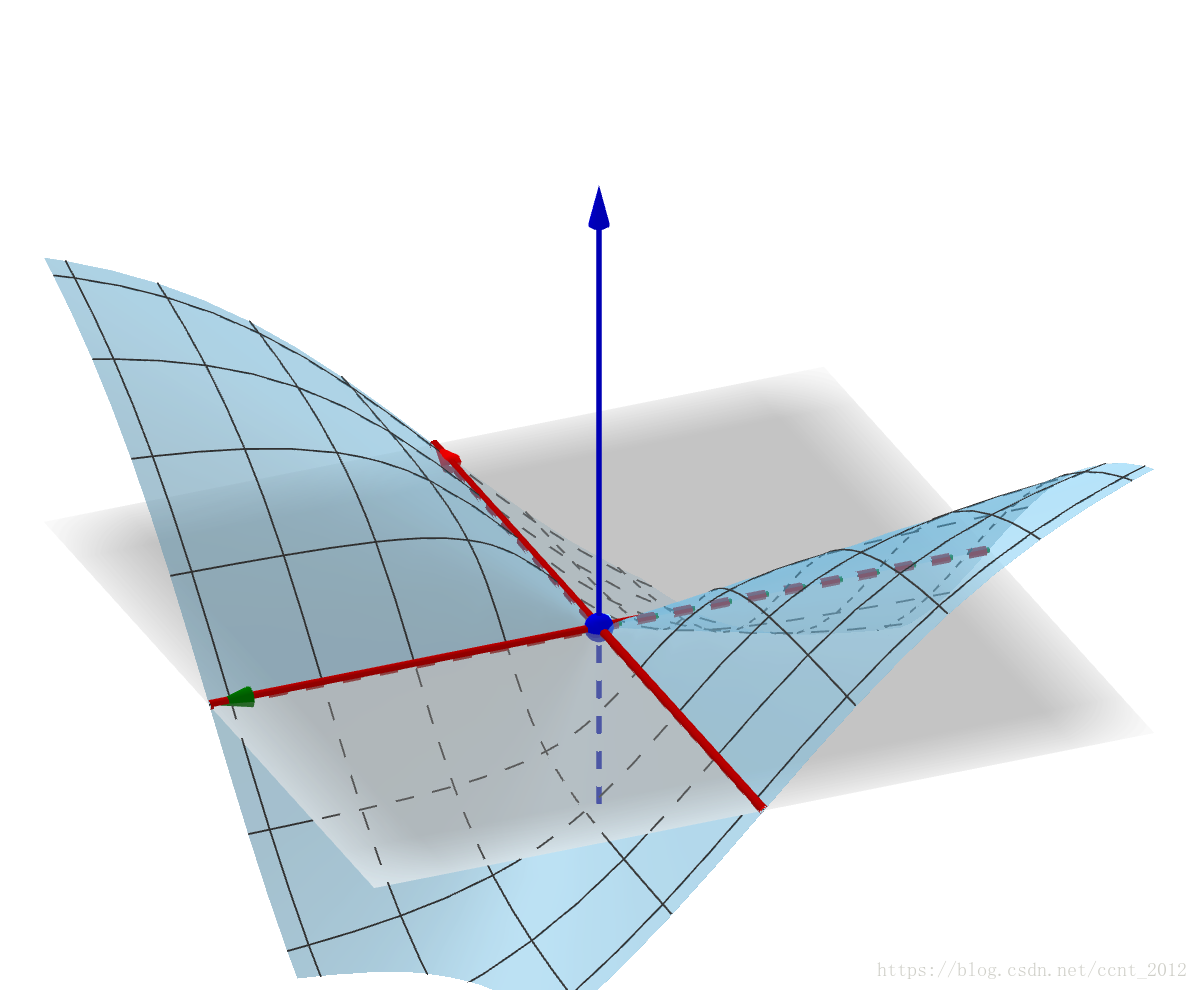
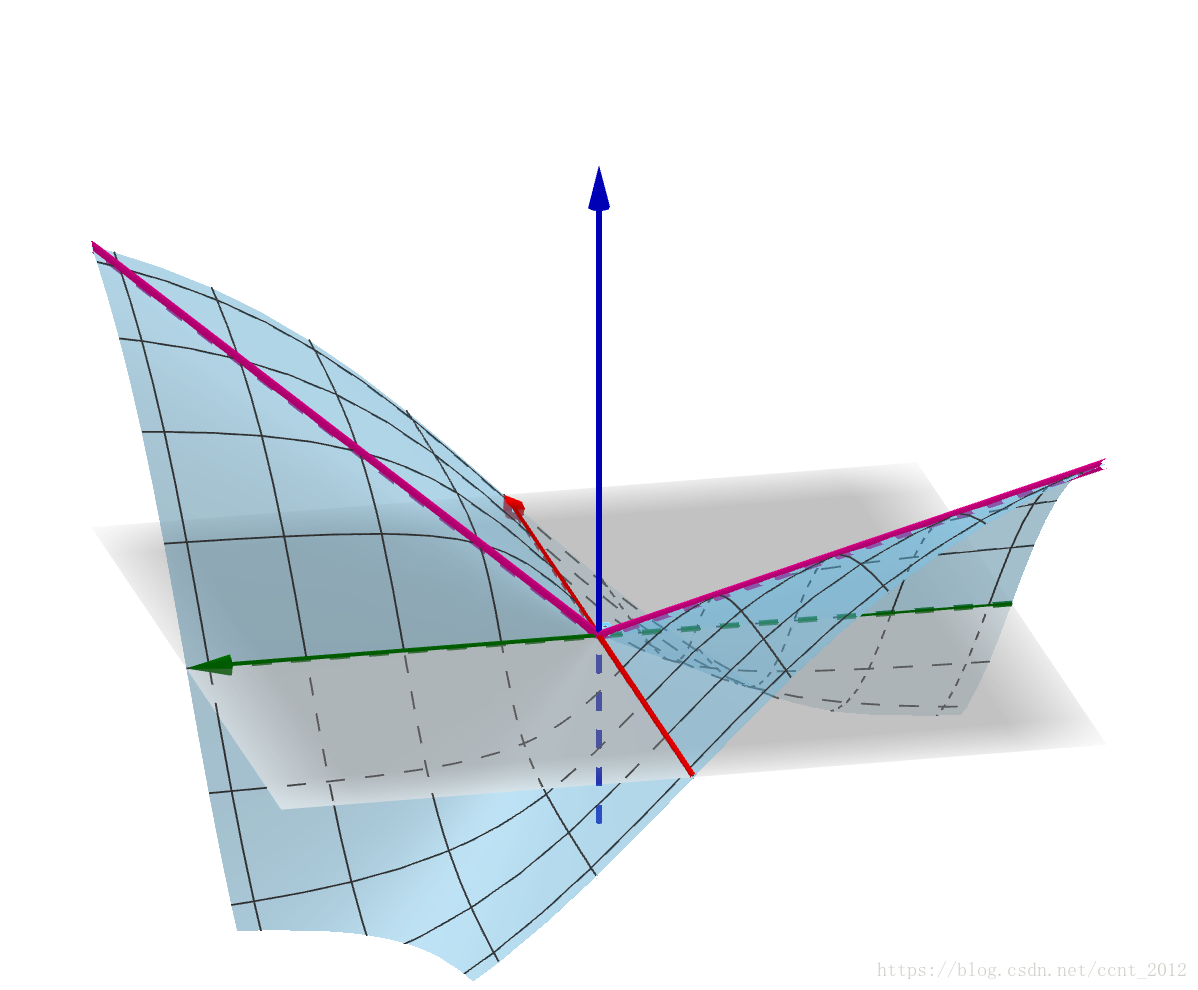
在(0,0,0) 点，f(x,y) 与x=0,y=0 的交线是下面红色的直线，分别与x 轴和y 轴重叠：

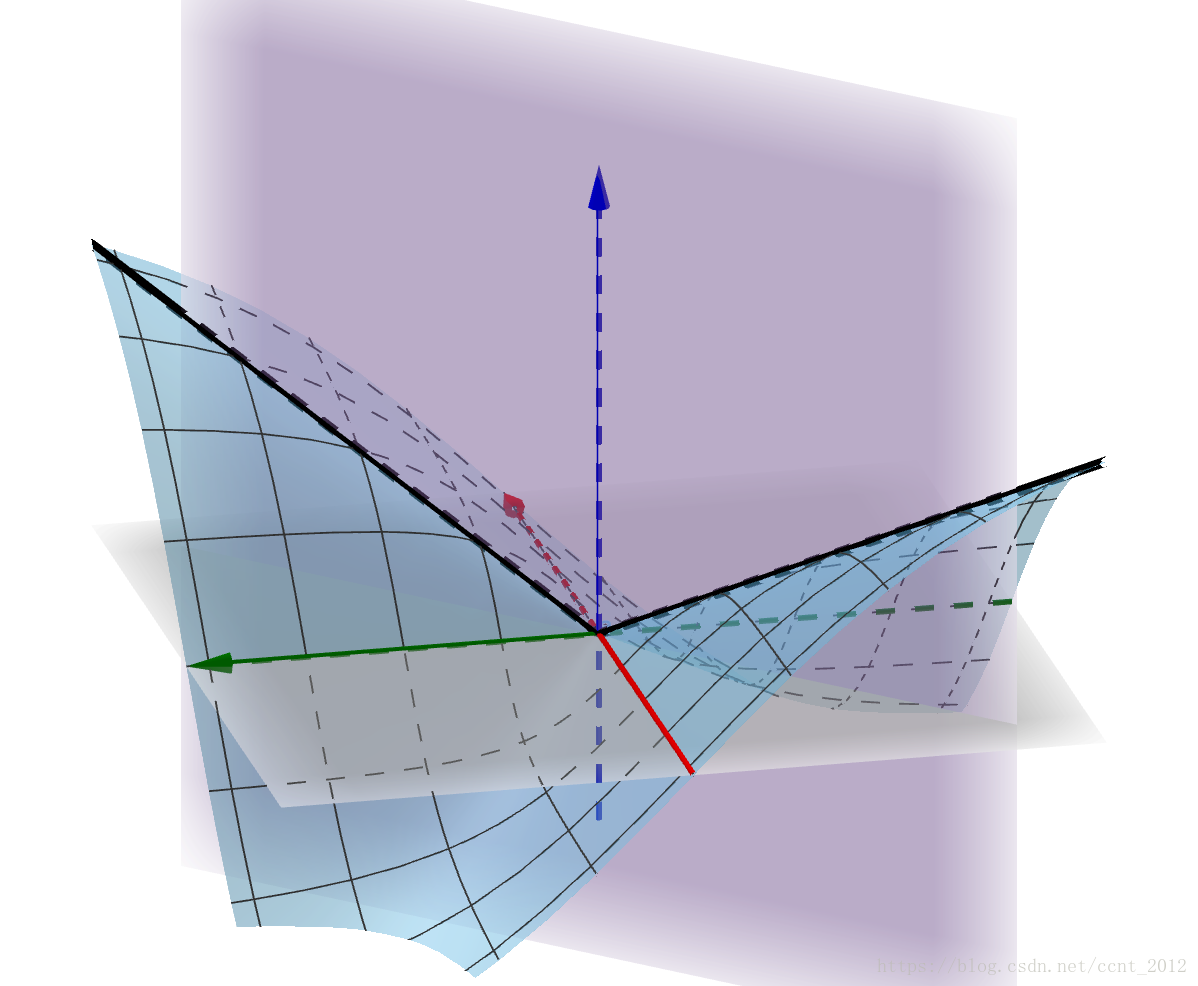
因此，在(0,0,0) 点的偏微分就是x 轴和y 轴。但是f(x,y) 与y=x 的交线是：