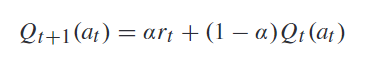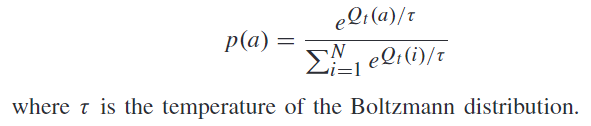根据学习曲线斜率的绝对值自动课程学习：Teacher–Student Curriculum Learning

Abstract

我们提出了教师-学生课程学习(TSCL)，这是一个自动课程学习的框架，在这个框架中，学生尝试学习一项复杂的任务，然后教师自动从给定的任务集中选择子任务让学生进行训练。描述一个教师算法家族，这些算法依赖于直觉，即学生应该多练习那些进步最快的任务，即学习曲线斜率最高的地方。此外，教师算法通过选择学生表现变差的任务来解决遗忘问题。展示了TSCL在两个任务上匹配或超过了精心手工制作的课程的结果:具有长短期记忆(LSTM)的十进制数字加法和Minecraft中的导航。自动设定的次序迷宫课程能够解决一个在直接训练时根本无法解决的《我的世界》迷宫，而且学习速度比对这些次迷宫进行统一采样要快一个数量级。
Index Terms：ctive learning, curriculum learning, deep reinforcement learning, learning progress.

I. INTRODUCTION

深度强化学习算法被用于解决视频游戏[1]、运动[2]、[3]、机器人[4]中的困难任务。然而，像“机器人，在会议室里把椅子布置成一个圆圈”这样奖励稀疏的任务，仍然很难直接应用这些算法来解决。其主要原因是实现奖励的时间步数太多，这对学分分配（哪一项行动有助于获得奖励）和探索（下一步将采取哪些行动）都是挑战。例如，我们知道解决一个随机探索任务所需的样本数量会随着获得奖励的步骤数量呈指数增长[5]。克服这个问题的一种方法是使用课程学习[6]–[9]，在这个课程中，课程的难度是递增的，只有在掌握了较容易的任务后，才对较难的任务进行训练。课程学习有助于在掌握一项简单任务后，通过本地探索发现更困难任务的策略。
要使用课程学习，研究者必须：

1. 能够按难度对子任务进行排序。
2. 确定掌握门槛。这可以基于达到一定的分数[7]、[9]，这需要对每个任务的可接受性能的先验知识。或者，这可能是基于性能的平稳期，由于学习曲线中的噪声，很难检测到这种平稳期。
3. 不断地把较容易的任务混在一起，同时学习更难的任务，以避免遗忘。设计这些混合物是[7]的一大挑战。

在本文中，我们介绍了一种新的方法——教师-学生-课程学习(TSCL)。这个学生是被训练的模型。教师监控学生的训练进度，并在每个训练步骤中确定学生应完成的训练任务，以使学生在课程中取得最大的进步。学生可以是任意的机器学习模型。教师在给学生布置任务的同时也在了解学生，这都是一个单一训练流程的一部分。
我们描述了几种基于学习进度[10]概念的教师算法。
其主要思想是学生应该练习更多进步最快的任务，即学习曲线斜率最高。为了防止遗忘，学生也应该练习那些表现越来越差的任务，比如，学习曲线斜率为负时。
本文的主要贡献如下。

1. 我们将TSCL，一个教师-学生的课堂学习框架形式化为部分可观察的马尔可夫决策过程（POMDP）[11]。
2. 我们提出了一系列基于学习进度概念的算法。该算法还解决了忘记先前任务的问题。
3. 我们评估了监督式和强化式学习任务的算法:具有长短期记忆(LSTM)的十进制数字加法和Minecraft中的导航。

II. TEACHER–STUDENT SETUP

图1展示了师生互动。在每一个时间步，老师为学生选择练习的任务。

学生在这些任务上进行训练，然后返回一个分数。老师的目标是让学生用尽可能少的训练步骤完成最后一项任务。

例如，分数可以是强化学习中的整体奖励或监督学习中的验证集准确性。
我们将教师帮助学生学习最终任务的目标正式化为解决POMDP[11]。POMDP将Markov决策过程（MDP）[12]扩展到整个系统状态不可见的情况下，必须根据系统状态的局部视图（观察）做出决策。
我们提出了两种POMDP的范式:

1. 简单，最适合强化学习;
2. 批量，最适合监督学习。

A. Simple POMDP Formulation

简单的POMDP范式暴露学生在单一任务上的分数，非常适合于强化学习问题。

1. 状态 $s_t$ 表示学生的整个状态(即。例如，神经网络参数和优化器状态)，对教师来说是不可观察的。
2. 动作对应于老师选择的任务参数。在下面，我们只考虑离散任务参数化，即教师从 $n$ 个子任务中选择一个。采取行动意味着对学生进行一定次数的迭代训练。
3. 观察状态 $o_t$ 是学生们在时间步 $t$ 上训练的任务 $a$ 的分数 $x_t^{a_t}$ 比如这一段的总奖励。虽然在理论上，老师也可以观察学生状态的其他方面，比如网络权重，但为了简单起见，我们选择只暴露分数。
4. 奖励 $r_t$ 是学生在时间步 $t$ 上训练的任务的分数变化 $r_t=x_t^{a_t}-x_{t_i^{\prime }}^{a_t}$ ,其中 $x_{t_i^{\prime }}^{a_t}$ 为同一的任务被训练时的上一个时间步。

B. Batch POMDP Formulation

在监督学习中，一批训练可以包括多个任务。这推动了POMDP的批范式。

1. 状态 $s_t$ 表示学生的训练状态。
2. 动作 $a_t$ 表示 $N$ 个任务上的概率分布。根据分布对每个训练批次进行采样 $a_t=(p_t^1,...,p_t^N)$ ,其中 $p_t^{(i)}$ 是时间步 $t$ 上任务 $i$ 的概率。
3. 观察状态 $o_t$ 是所有任务训练后的得分 $o_t=(x_t^1,...,x_t^N)$ 。在最简单的情况下，分数可以是在训练集上计算出的任务的准确度。然而，在小批量训练的情况下，模型会在训练过程中演化，因此，在训练步骤之后，无论如何都需要额外的验证集评估来产生一致的结果。因此，我们使用一个单独的验证集，它包含所有任务的统一组合来生成这些分数。
4. 奖励 $r_t$ 是上一个时间步骤中评估分数变化的总和：$r_t={\sum }_{i=1}^N{x}_t^{(i)}-x_{t-1}^{(i)}$
   这种设置也可以用于强化学习，通过批量地执行训练。然而，由于在强化学习中为一个样本(一个片段)打分的计算成本通常比在监督学习中要高得多，因此使用简单的POMDP公式并在每个训练步骤后立即决定下一个任务是有意义的。

C. Optimization Criteria

对于其中任一POMDP范式，最大化教师事件的总奖励等于在训练结束时最大化所有任务的分数 ${\sum }_{t=1}^T{r}_t={\sum }_{i=1}^N{x}_{T_i}^{(i)}$ ，其中 $T_i$ 是任务 $i$ 最后一个训练步。（由于伸缩求和抵消了除 $T_i^{th}$ 外所有的 $x_t^{(i)}$）
虽然优化标准的一个明显选择是在最后的任务中的表现，但最初，学生可能在最后的任务中没有任何成功，这并没有向老师提供任何有意义的反馈信号。因此，我们选择最大限度地提高所有任务的性能总和。这里的假设是，在课程学习中，最终任务包含了之前所有任务的要素;因此，在中间环节的良好表现通常会导致在最终任务中的良好表现。

III. ALGORITHMS

POMDPs通常使用强化学习算法来解决。然而，这需要许多训练片段，而我们的目标是在一个教师片段中训练学生。因此，我们采用更简单的启发式方法。最基本的直觉是，学生应该多练习那些取得最大进步的任务，同时也要练习那些有被遗忘风险的任务。

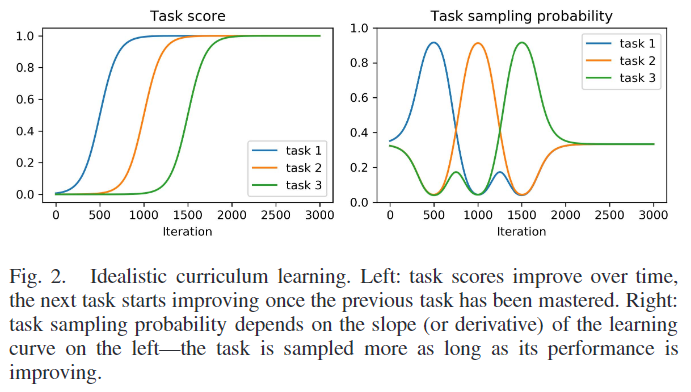
图2显示了在课堂学习设置中理想的训练进度演示如下。

1. 首先，教师没有知识，所以均匀地从所有任务中抽取样本(迭代0)。
2. 当学生开始在任务1上取得进展时，老师会给这个任务分配更多的概率质量(迭代次数为250-750次)。
3. 当学生掌握了任务一，它的学习曲线就变平了，老师也减少了对任务的采样。此时，学生也开始在任务2上取得进展，所以老师从任务2中采样更多内容(迭代750-1250次)。
4. 这一直持续到学生掌握所有任务（迭代2000）。当所有的任务学习曲线在最后变平时，教师回到任务的统一抽样（迭代2000-3000）。

图2所示的过程是理想的，因为在实践中经常会发生遗忘。例如，当大部分概率分配给任务2时，任务1的性能可能会变差。为了解决这个问题，学生也应该练习所有学过的任务，特别是那些遗忘发生的任务。为此，我们根据学习曲线斜率的绝对值对任务进行采样。如果分数的变化是负的，这一定意味着遗忘发生了，这个任务需要更多的练习。
仅凭这种直观的描述并不能说明一个算法。我们需要提出一种从噪声任务分数估计学习曲线斜率的方法和一种平衡探索与开发的方法。我们从非静态多武装强盗问题[13]的算法中获得灵感，并将其应用于TSCL。为简洁起见，我们在这里只给出简单范式算法的描述，批量范式算法可以在附录A中找到。

A. Online Algorithm

在线算法(见算法1)的灵感来自基本的非平稳强盗算法（ nonstationary multi-armed bandit problem ）[13]。它使用指数加权移动平均线来跟踪不同任务的预期收益 $Q$ ,



或者，可以使用玻尔兹曼分布来选择下一个任务

B. Naive Algorithm

为了更可靠地估计学习进度，一个人应该多次练习这个任务。朴素算法(见算法2)每完成一次任务，观察得到的分数，然后用线性回归估计学习曲线的长度。在上述的非平稳bandit算法中，采用回归系数作为奖励。

C. Window Algorithm

重复一项任务，固定的次数是昂贵的，但毫无进展。窗口算法(见算法3)为每个任务保存last K scores的FIFO缓冲区，以及记录这些分数时的时间步长。以时间步长为输入变量，用线性回归方法估计每个任务的学习曲线斜率。在上述非平稳bandit算法中，用回归系数作为修正。

D. Sampling Algorithm

前面的算法需要调优超参数来平衡探索。为了摆脱勘探超参数，我们从汤普森采样中得到了启发。抽样算法(见算法4)为每个任务保留一个lastKrewards缓冲区。为了选择下一个任务，从每个任务的 k-last-reward buffer中采样最近的奖励。然后，无论哪个任务产生了最高的抽样奖励就选择哪个。这使得探索成为算法中很自然的一部分:最近获得高回报的任务更容易被采样。

IV. EXPERIMENTS

A. Keylock MDP

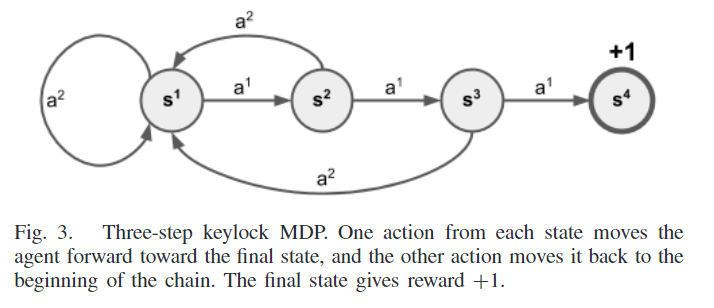
Keylock MDP[5]是一个简单的任务，对于当前的强化学习方法来说是一个挑战。N步Keylock MDP（见图3）基本上是一个状态链加上最终状态。
对于每个非最终状态，代理可以采取两个动作:一个将代理向前移动到下一个状态，另一个将代理移动到链的开始位置。当代理到达最后状态时将获得+1奖励。
由于代理在到达最终状态之前不会获得任何奖励，因此它第一次最多只能进行随机探索。
很容易看出，对于一般情况，它需要 $2^n$ 个事件来尝试所有状态下可能的行为组合，然后才能到达那里。因此，求解该MDP所需的时间与链的长度 $n$ 成指数关系。

我们使用表Q-learning[14]与玻尔兹曼探索作为学生算法(详见附录B)。我们这个实验的目的是要证明算法能从课程任务的最终状态逆向恢复自然排序。此外，它展示了算法背后的主要直觉，它从简单的任务开始，通过有限的探索就可以找到解决方案，然后逐步进行更复杂的任务，只需要局部探索就可以为之前解决的任务奠定解决方案。

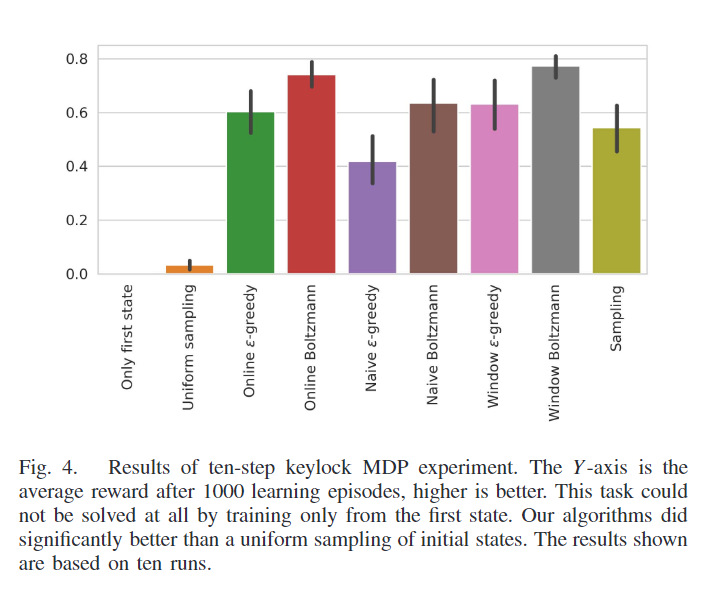
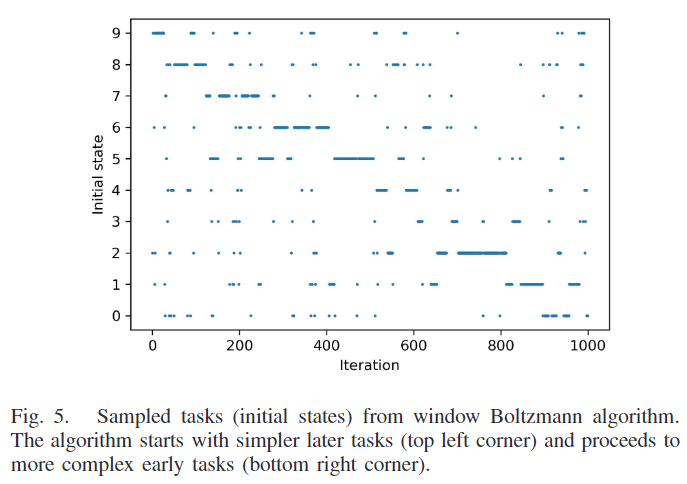
图4显示了10步keylock MDP在1000 episodes 之后的平均奖励。这个任务在1000 episodes 里都是无法解决的，因为它们只从第一个状态 $s^1$ 开始。我们的算法都比初始状态的均匀采样要好得多。图5显示了在一个训练过程中选择的任务(初始状态)的例子。图上的对角线表示所发现的课程与直觉相符。

B. Decimal Number Addition

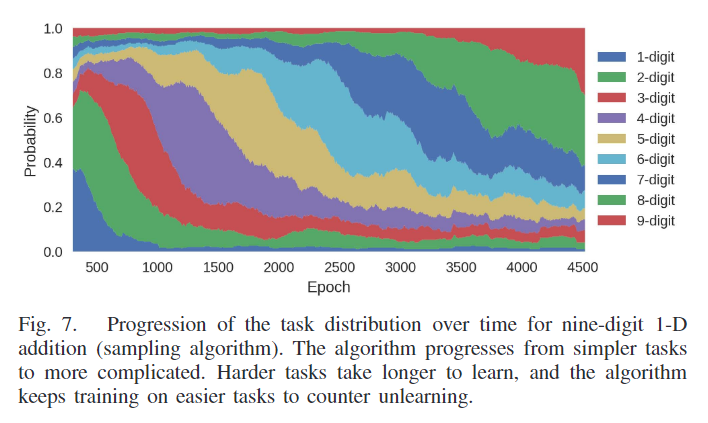
使用LSTM进行十进制数的加法运算是一项众所周知的任务，需要在合理的时间内完成。它被实现为序列对序列模型[15]，其中网络的输入是由一个加号分隔的两个十进制编码的数字，网络的输出是这些数字的总和，也是索引编码。课程是基于输入数字的位数，学习简短数字的加法更容易，然后学习较长的数字。数字加法是一个有监督的学习问题，因此，可以通过在小批量中包含多个课程任务来更有效地训练。因此，我们采用第II-B节所述的批量训练方案。我们使用的分数是在验证集上计算的每个任务的准确性。计算结果为三组不同随机种子的均值和标准差。完整的实验细节见附录C。

V. RELATEDWORK

Bengio等人的工作。[6] 激发了人们对学习curricu lum的普遍兴趣。最近的结果包括学习如何执行短程序[7]，在图中找到最短路径[8]，以及学习如何玩第一人称射击游戏[9]。所有这些作品都依赖于人工设计的课程，而不是试图自动生成。使用学习进度作为奖励的想法可以追溯到[17]。它已经成功地应用在开发操作机器人的环境中，学习对象操作[18]，[19]，并在实际的教室环境中教小学生[20]。以学习进度作为奖励可以与内在动机[10]，[21]的概念相联系。最近，Sukhbaataret al.[22]提出了一种制定递增目标的方法，因此，自动设置课程。这一段由两个主体组成，爱丽丝和鲍勃，其中爱丽丝产生轨迹，而鲍勃试图重复或逆转它们。[23]中的类似工作使用生成对抗网络为代理生成目标状态。与TSCL相比，它们能够在运行中生成新的子任务，但这主要有助于探索，并不能保证帮助学习最终的任务。与我们最相似的工作是在[24]中并发完成的。尽管问题陈述惊人的相似，我们的方法不同。他们将自动课程学习仅应用于超视觉的序列学习任务，同时也考虑了强化学习任务。他们使用EXP3.S算法来对付对抗bandits，而我们提出了受非平稳bandits启发的替代算法。他们考虑其他基于复杂性增益的学习进度指标，而我们只关注预测增益(在他们的实验中总体表现最好)。它们并没有试图对抗遗忘，我们是通过使用预测增益的绝对值来实现的。此外，他们的工作只使用统一的任务采样作为基准，而我们比较的是最著名的手工课程的给定任务。总之，他们得出了非常相似的结论。
在[25]-[27]中也探讨了十进制加法，有时比[7]中的原始工作改进了结果。我们的目标不是提高加法结果，而是评估不同的课程方法；因此，没有直接的比较。
虽然探索奖励[30][32]解决了同样的稀疏奖励问题，但它们适用于学生算法，而我们正在研究不同的教师方法。由于这个原因，我们把比较留给以后的工作。
课程学习也成功地应用于半自由学习。[33]表明，标签传播算法从简单到困难的未标记样本排序中获益。样品的简洁性可以从其标签的可靠性和可辨性来估计。这些，反过来，可以通过使用学习模型[33]，通过评估标签[34]的噪声，通过使用多输入模式[35]，或者通过使用模型集合[36]来估计。这些方法不直接适用于监督或强化学习设置，他们没有利用学习进展或试图对抗遗忘，这是本工作的要点。

VI. CONCLUSION

我们提出了一个自动课程学习的框架，可用于监督和强化学习任务。我们基于学习进度的概念，在该框架内提出了一系列算法。尽管许多算法的表现同样出色，但在选择任务时，依赖学习曲线斜率的绝对值是至关重要的。这保证了对网络开始遗忘的任务进行再训练。在我们的LSTM十进制加法实验中，采样算法优于最好的手工设计课程和均匀采样。对于需要学习课程的问题，TSCL可以避免排序子任务的困难和手工设计课程的单调乏味。

VII. FUTUREWORK

为了简单起见，我们在本工作中只考虑离散任务参数化。同样的思想也可以应用于连续的任务参数化，方法是用高斯分布或混合高斯分布代替离散的分类分布。另一个值得探索的有希望的想法是在没有预先定义子任务的情况下使用自动学习。例如，子任务可以从生成模型中采样，也可以从同一环境中的不同初始状态中获取。

今天的文章根据学习曲线斜率的绝对值自动课程学习：Teacher–Student Curriculum Learning分享到此就结束了，感谢您的阅读。