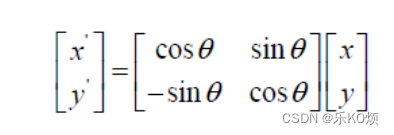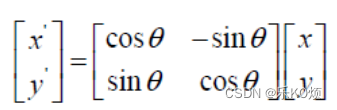1.向量旋转矩阵和坐标旋转矩阵区别
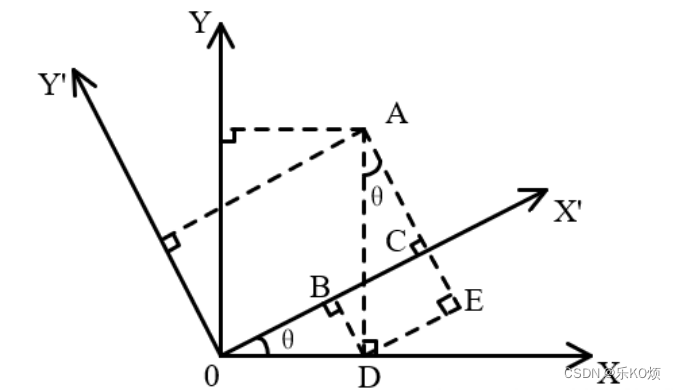
坐标旋转:
坐标旋转对应的是点在另一个坐标系的位置,设点A在xoy中为(x,y),在坐标系x’oy’下坐标是(x’,y’),旋转角度由x向y,逆时针旋转。则他们关系是:
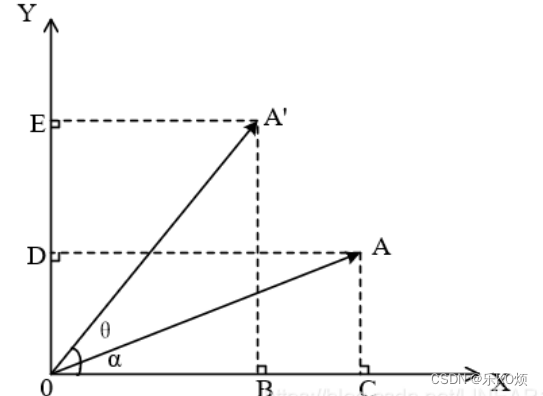
向量旋转:
设A向量为(x,y),A’向量为(x’,y’),则他们关系是:
总结:
向量旋转和坐标旋转不一样,且互逆。
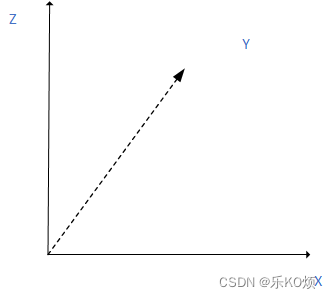
2. 三维坐标旋转
如下图所示三维坐标系是右手坐标系,我们常用的坐标系也是右手坐标系。
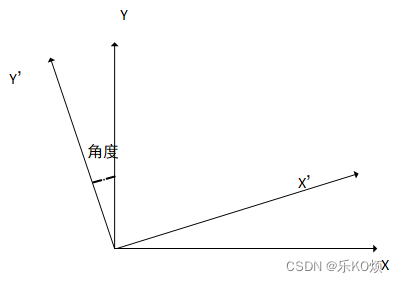
拆开,每两个维度分析:
[ x ′ y ′ z ′ ] = [ c o s ( θ ) s i n ( θ ) 0 − s i n ( θ ) c o s ( θ ) 0 0 0 1 ] [ x y z ] \begin{bmatrix} x’ \\ y’ \\z’ \end{bmatrix} = \begin{bmatrix} cos(\theta) & sin(\theta)& 0 \\ -sin(\theta) & cos(\theta)&0 \\ 0& 0&1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} ⎣⎡x′y′z′⎦⎤=⎣⎡cos(θ)−sin(θ)0sin(θ)cos(θ)0001⎦⎤⎣⎡xyz⎦⎤
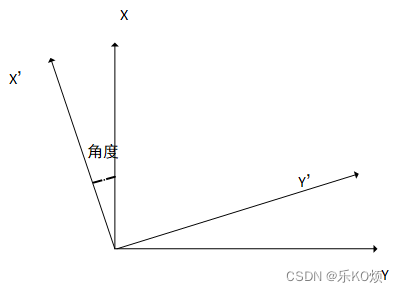
同理对于yoz平面来说,顺时针旋转坐标,如下图
变换方程为:
[ x ′ y ′ z ′ ] = [ 1 0 0 0 c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) ] [ x y z ] \begin{bmatrix} x’ \\ y’ \\z’ \end{bmatrix} = \begin{bmatrix} 1&0& 0 \\ 0 &cos(\theta) & -sin(\theta)\\ 0& sin(\theta) & cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} ⎣⎡x′y′z′⎦⎤=⎣⎡1000cos(θ)sin(θ)0−sin(θ)cos(θ)⎦⎤⎣⎡xyz⎦⎤
但对于如下图所示的左手坐标系来说:是不同的
变换方程为:
[ x ′ y ′ z ′ ] = [ − s i n ( θ ) c o s ( θ ) 0 c o s ( θ ) s i n ( θ ) 0 0 0 1 ] [ x y z ] \begin{bmatrix} x’ \\ y’ \\z’ \end{bmatrix} = \begin{bmatrix} -sin(\theta) & cos(\theta)&0 \\ cos(\theta) & sin(\theta)& 0 \\ 0& 0&1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} ⎣⎡x′y′z′⎦⎤=⎣⎡−sin(θ)cos(θ)0cos(θ)sin(θ)0001⎦⎤⎣⎡xyz⎦⎤
今天的文章二维,三维坐标旋转,左右手坐标系的区别_三维空间坐标的旋转算法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/86885.html