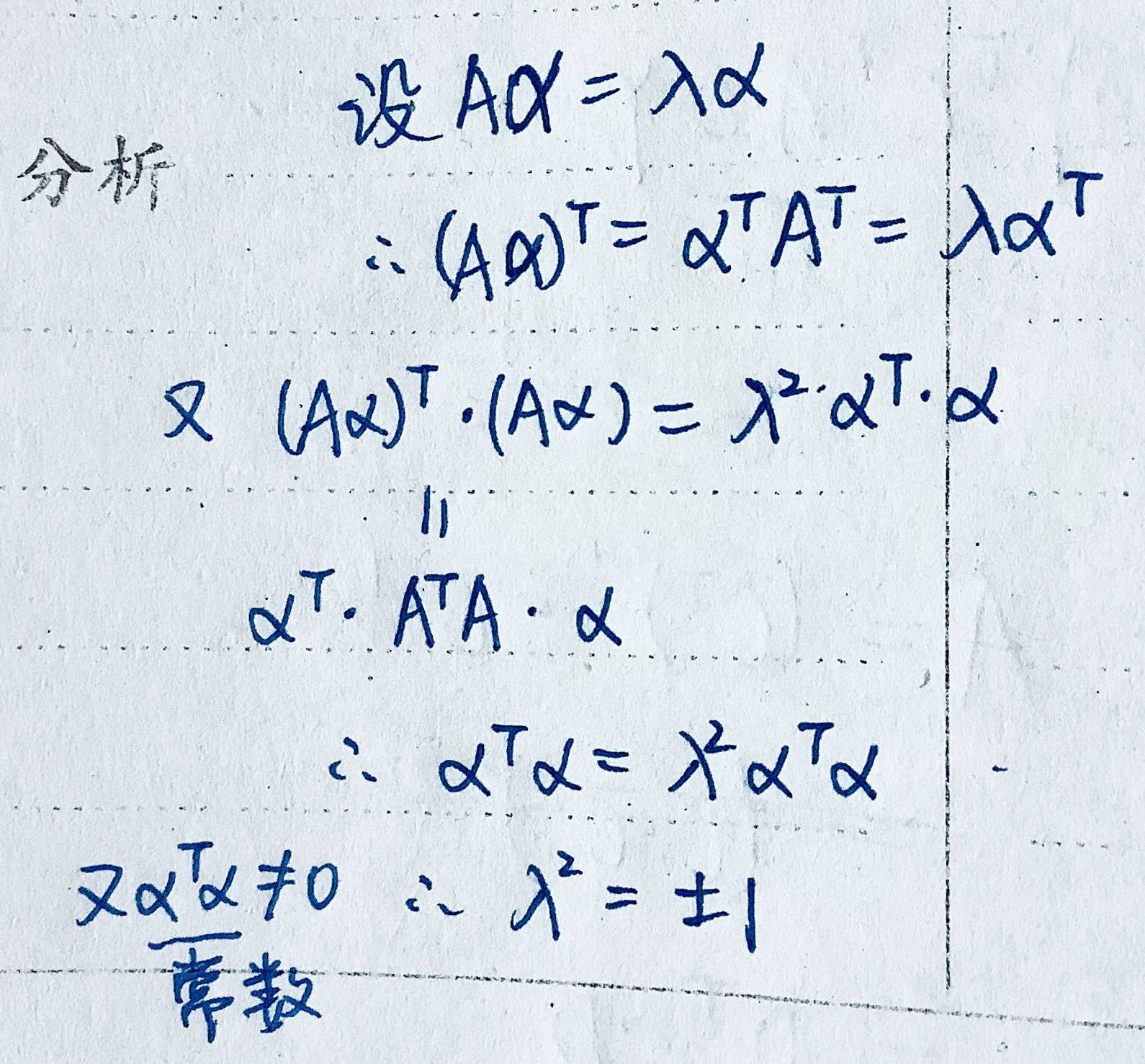对角矩阵可逆的充分必要条件_怎么判断矩阵是否可逆

一、可逆矩阵

1. 定义

给定一个n阶方阵A，若存在一n阶方阵B使得AB=BA=E（或AB=E、BA=E任满足一个），E是单位矩阵，则称A可逆，B是A的逆矩阵。

2. 充要条件

（⇔表示等价于，在这里把类似角度的条件放一起了）

（1）定义。AB=E；

（2）r(A)=n（满秩矩阵）  ⇔   |A|≠0    ⇔    λ 全不为0；

（3）PAQ=E（A等价于n阶单位矩阵）   ⇔    A=P1P2…Pn（可表示成初等矩阵的乘积）；

（4）AX=0 仅有零解   ⇔    AX=b 有唯一解；

（5）A的行（列）向量组线性无关   ⇔    任一n维向量可由A的行（列）向量组线性表示。

注：实对称矩阵未必可逆！如对角矩阵diag(1,1,0)。

《方阵A可逆的充要条件是》：https://zhidao.baidu.com/question/513426402.html

二、初等矩阵

1. 定义

指由单位矩阵经过一次初等变换得到的矩阵。

2. 可逆矩阵与初等矩阵

（1）初等矩阵都是可逆矩阵。

（2）判断 A 是否是可逆矩阵，有一个充要条件是，A可表示成初等矩阵的乘积。（见1.中链接）现对此做出说明。

充分性：初等矩阵都是可逆矩阵，是满秩的。而初等矩阵的乘积相当于，对一个最开始的初等矩阵B做了一系列初等行/列变换，而初等变换不改变矩阵的秩，所以该乘积所得矩阵是满秩的，即A可逆。

必要性：考虑初等行变换法求某矩阵 C 的可逆矩阵，则需要写成 (C | E)，然后将左侧变为E，此时右侧的C-1是E经过了多步初等行变换而得，也即是多个初等矩阵的乘积，那么也就是逆矩阵可以表示为多个初等矩阵的乘积。不妨将C-1看作可逆矩阵D，所以可逆矩阵一定可以表示为初等矩阵的乘积。

《可逆矩阵A总可以表示若干初等矩阵的乘积，怎么证明》：https://zhidao.baidu.com/question/985682018865592779.html

三、分块矩阵

针对分块矩阵能否相似对角化问题，有如下结论。（证明及例题见链接）

分块矩阵相似对角化的充要条件是，子块可对角化。所以转为分别求子块的特征值和特征向量，最终将特征向量拼成分块矩阵。

《分块矩阵的对角化分析》：http://mtoutiao.xdf.cn/kaoyan/201611/10564800.html

四、正交矩阵

1. 定义

满足  的矩阵。

2. 充要条件

（1）定义。   ⇔    ；

（2）P由规范正交基组成；

（3） 都是正交矩阵。

3. 性质

（1）|P|=1 或 -1（由定义得）；

（2），（由规范正交基得）；

（3）λ=1 或 -1，但具体几重需要另求。

证明思路[1]. 由，得，即1/λ=λ；

[2]. 逐步化简。

今天的文章对角矩阵可逆的充分必要条件_怎么判断矩阵是否可逆分享到此就结束了，感谢您的阅读。