假设检验的流程及步骤_假设检验包括哪些类型

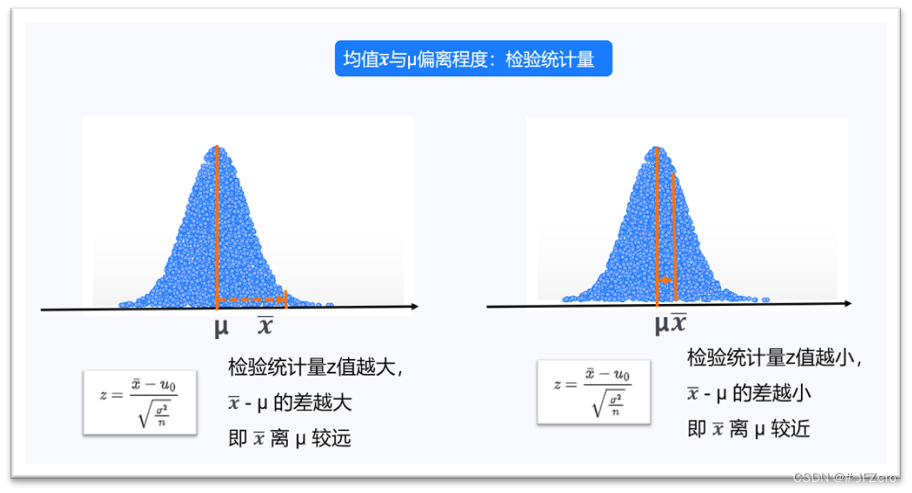
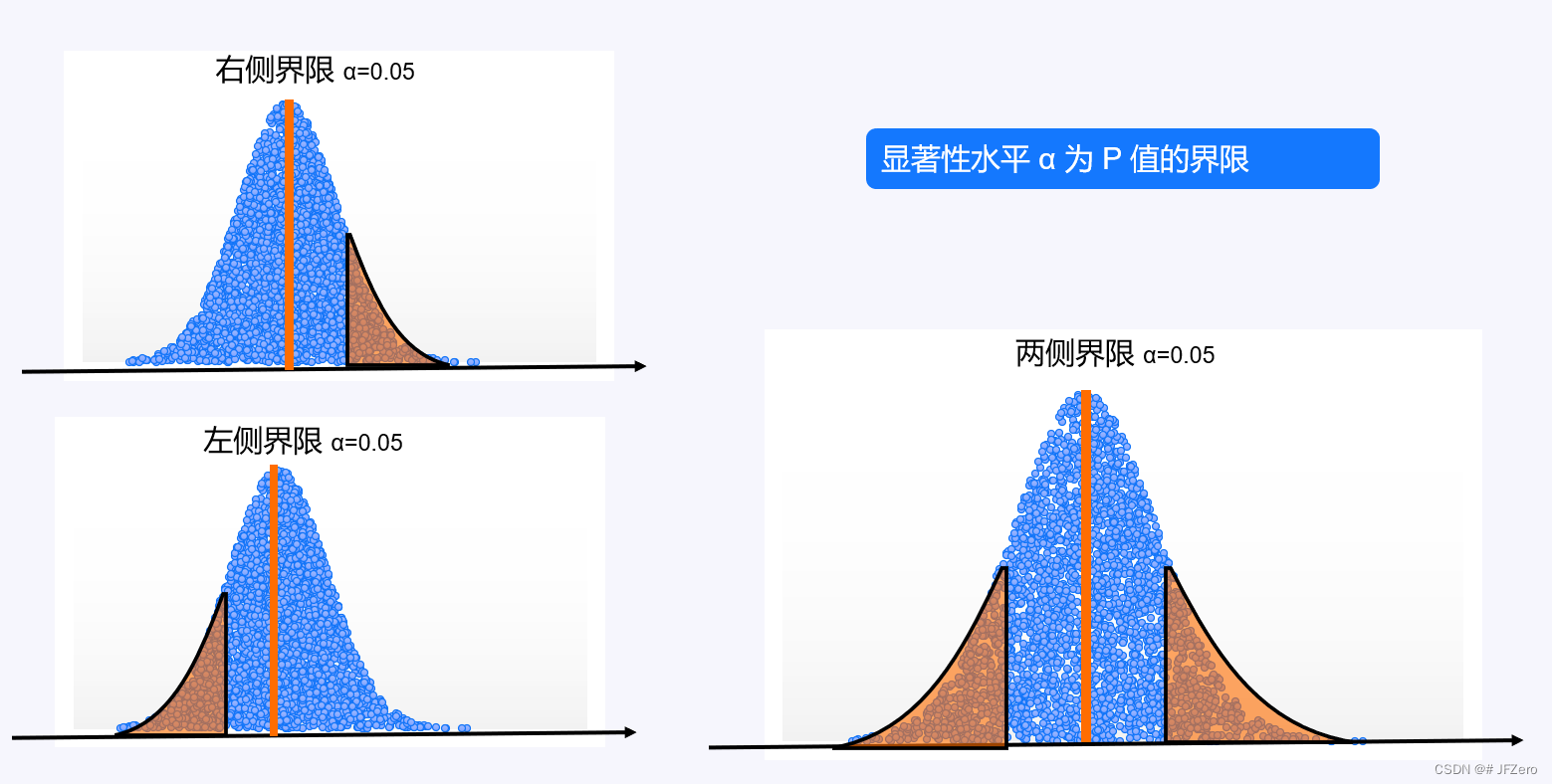
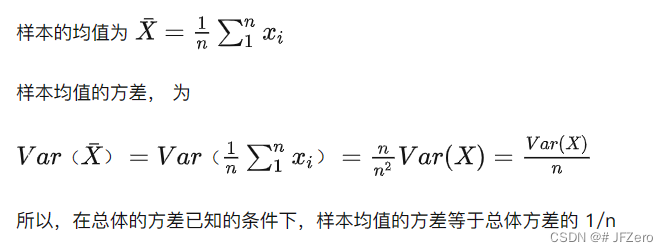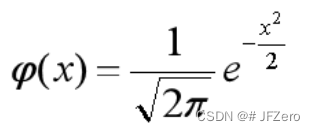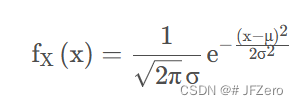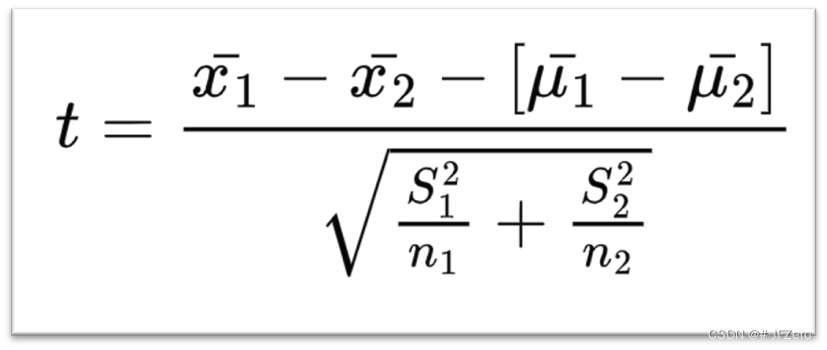假设检验的检验流程： ① 提出假设 ②计算检验统计量 ③ 计算 P 值 ④ 规定显著性水平 ⑤ 判断显著性

0、假设检验简介

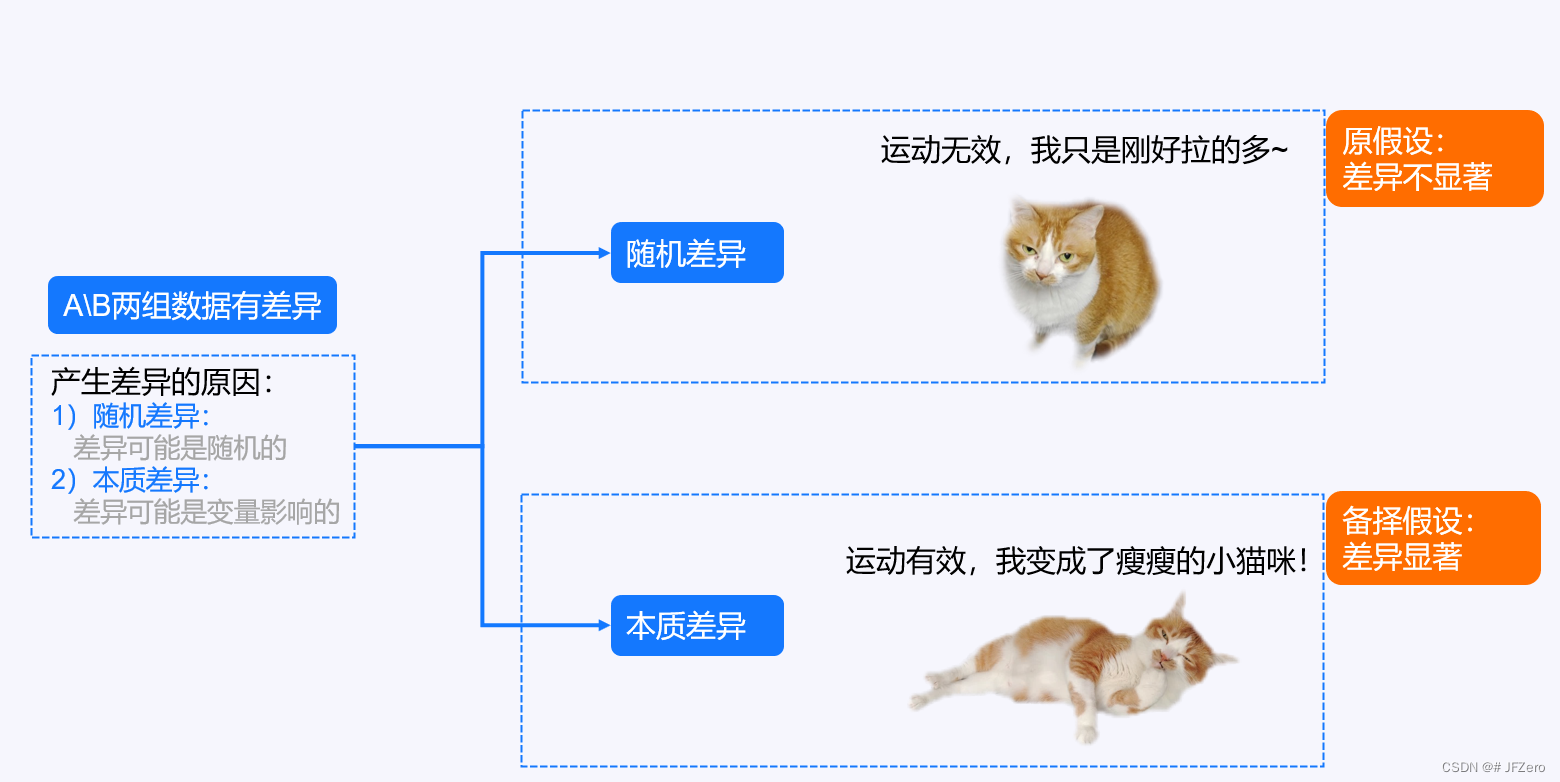
假设检验应用了推理思维，主要通过提出假设、验证假设、得出结论这三个步骤完成分析：

1）首先提出假设，对数据差异的显著性提出假设；
2）其次验证假设，通过统计学中的显著性检验，寻找数据差异显著的证据；
3）最后得出结论，根据显著性检验结果，判断数据差异是随机误差，还是本质差异。

接下来，我们将逐一认识各流程，并实现猫咪运动减肥的ABtest案例。

首先是提出假设。

1. 提出假设

• 提出假设，是对数据差异的显著性提出假设。

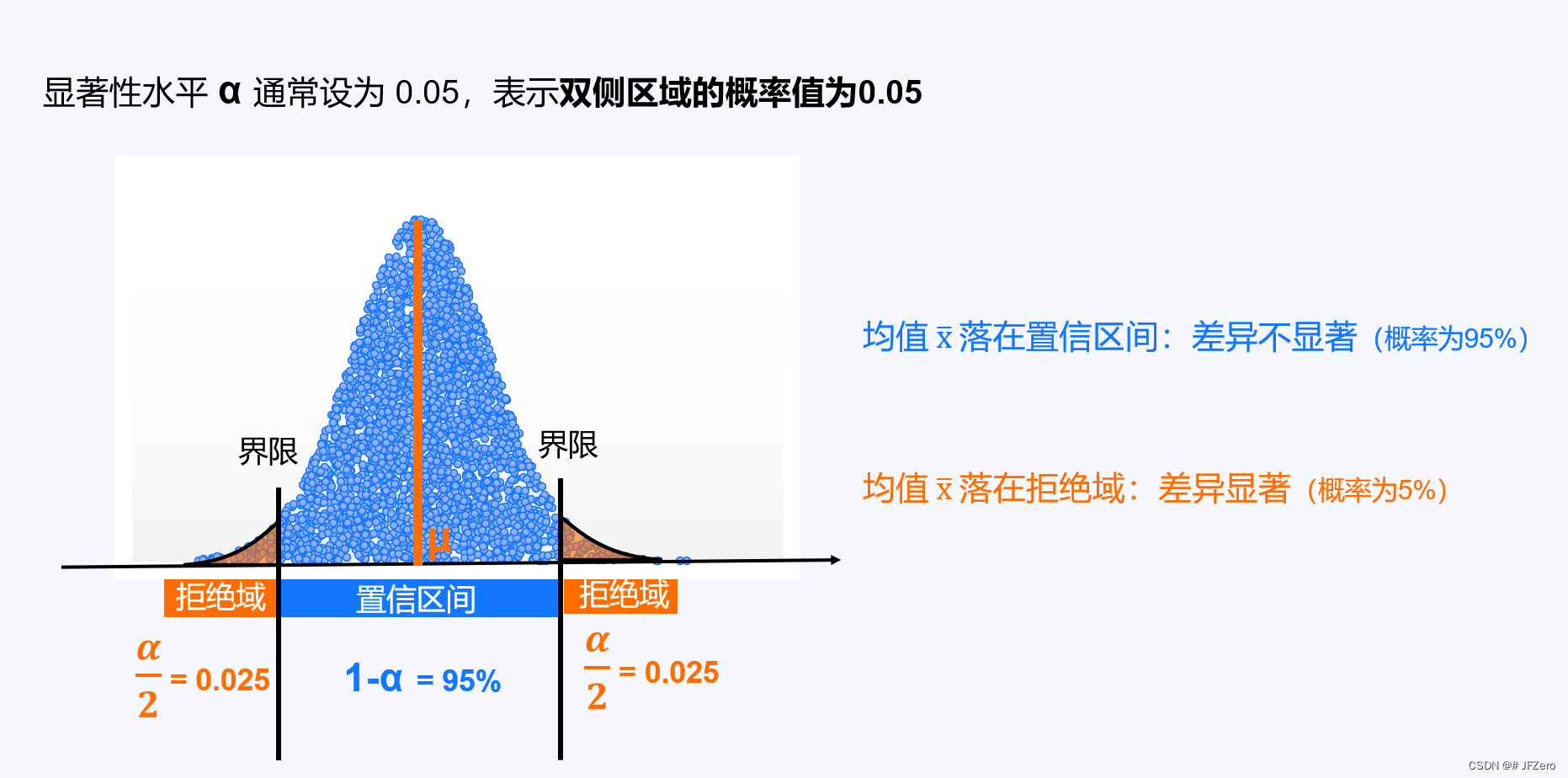
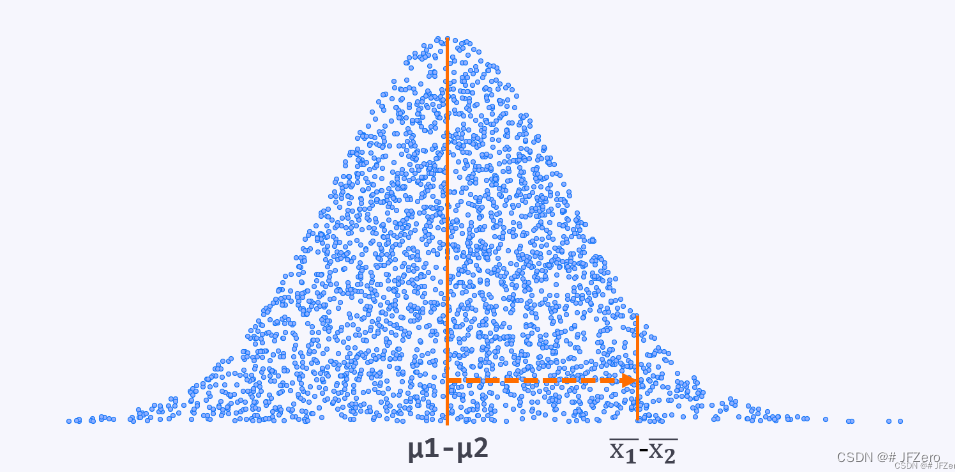
在正态分布中，数据之间的差异，
👉有较大概率是落在置信区间里，此时认为差异不显著；
👉极小概率是落在拒绝域里，被认为是本质差异，此时认为差异显著。

1.1 假设的内容

👉假设检验应用反证法的思想，先提出较大概率的差异不显著原假设，简称H0假设。

H0假设: μ1 = μ2（即假设差异不显著，总体均值相等）

注意：μ1、μ2表示总体均值，在单样本、双样本检验中，有不同的解读。
1）单样本：当假设“样本与总体（检验的总体）差异不显著”时，表示样本和总体没有本质区别，即样本来自总体，一般设为μ = μ0；
2）双样本：当假设“两个样本 差异不显著”时，通常表示这两个样本背后的总体，实际没有本质区别；
即两个样本各自背后的两个总体，均值相等——总体均值相等。

👉同时提出与原假设相反的备择假设，即极小概率的差异显著假设，也称H1假设。

H1假设：μ1 ≠ μ2（即差异显著）
1）单样本：样本与总体本质有差别，样本不是来自这个总体。
2）双样本：两个样本各自背后的总体，本质有差别，总体均值不相等。

1.2 判别假设的思路

• 当没有证据，能证明差异显著时，只能维持原假设H0，即认为应该是大概率的差异不显著。
• 当经过显著性检验，找到证据能证明差异显著时，才可以推翻原假设（H0)，接受备择假设（H1），认为差异是本质差异。

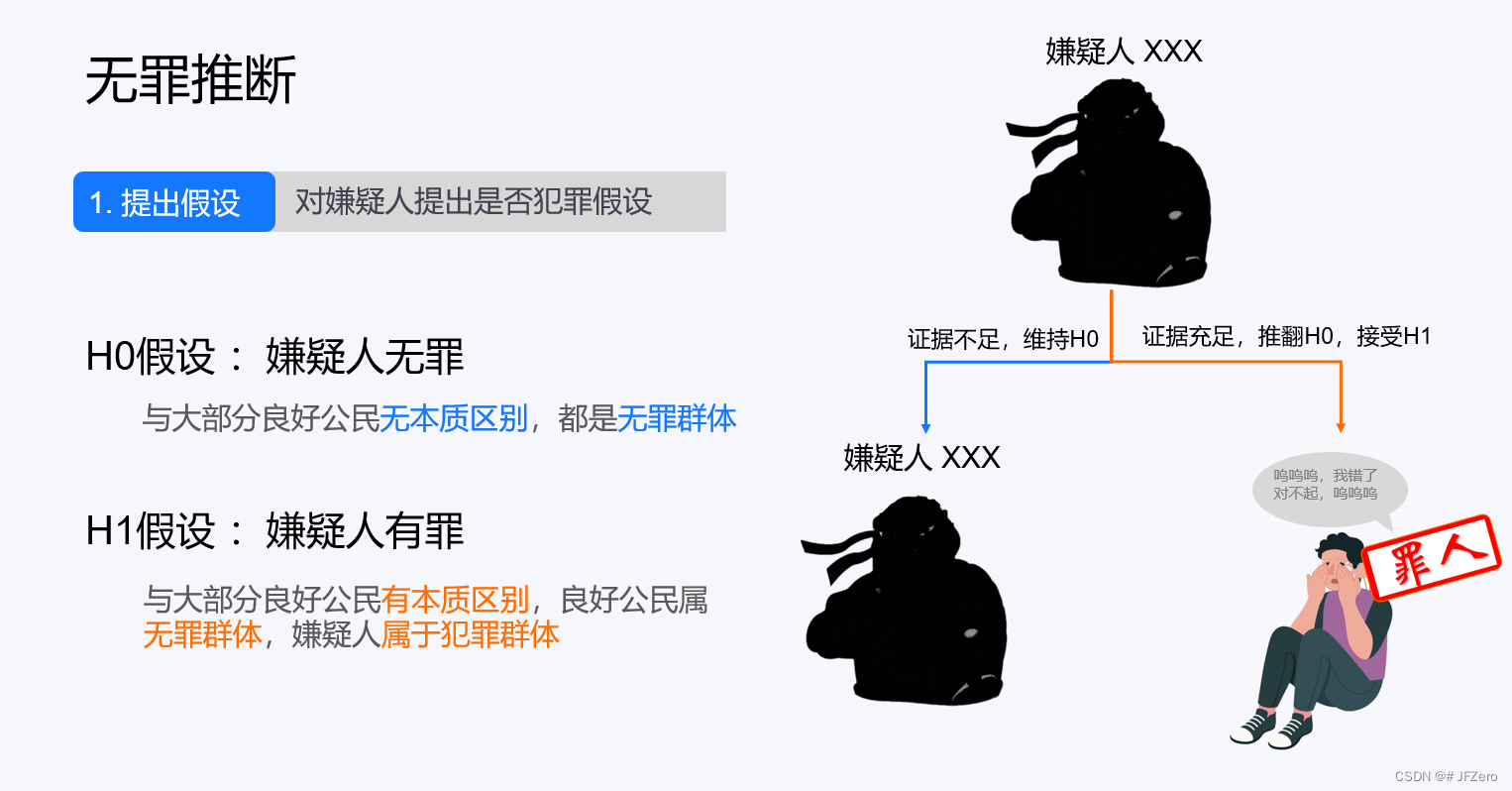
这就好像法律上的无罪推断原则：先假设犯罪嫌疑人和大多数良好公民一样，是无罪的。

犯罪证据不足，则无法判定你是否有罪，维持原本假设，你无需去踩缝纫机。
犯罪证据充足，则可以判定你有罪，推翻原本假设，立刻扭送你去踩缝纫机。

以大概率情况作为原假设，找到证据才能推翻原假设，这体现的是一种谨慎的推理思维，较大程度上避免了冤假错案。【但还是会发生冤假错案的，只不过概率减少了很多】

以反向思维做假设 ，看看两种思维的假设对比结果
反向思维——有罪推断原则：先假设犯罪嫌疑人和少数良好公民一样，是有罪的。
——【这时，你要去找无罪的证据】

• 你无法自证清白（找不到清白的证据），则无法判定你是否有罪，维持原本假设——有罪，你要去踩缝纫机。
• 你可以自证清白（找到清白的证据），则可以判定你无罪，推翻原本假设，你将无罪释放。

这会引发什么情况呢：所有人一出生，不管三七二十一，先判定为有罪，关进监狱里踩缝纫机。
所以，人类世界的法律，是不可以这样假设的！否则就是人间炼狱了

但这时，我有个强烈的困惑：人类世界行不通，难道统计学世界也行不通吗？
原假设为：差异显著（5%）
备择假设为：差异不显著（95%）
【找差异不显著的证据：

• 找不到差异不显著的证据：即最后计算出的 P 值<显著性水平α，说明随机差异概率非常小，则维持原假设
• 找到差异不显著的证据：即最后计算出的P 值>显著性水平α，说明随机差异概率较大，则推翻原假设，接受备择假设
  所以，在统计学世界里，假不假设的，还有什么意义：都是要靠显著性检验来判断结果的

之前有人说假设检验的假设，是基于小概率原理：即认为一次抽样不可能随机发生小概率事件

• 说实话，逆向假设也是不违背小概率原理的

所以，我认为假设检验之所以原假设为 μ1 = μ2，纯粹是因为这样的假设，能够计算检验统计量（差异程度）、概率P值！！！——因为显著性检验中，检验统计量的公式是基于μ1=μ2的前提下构造的。（要讲起这个，又是一番深深深深的挖掘了）

• 因此，假设检验的提出假设，其实是应用了反证法的思想：先按照原假设去计算，如果计算出的结果出问题，则说明原假设不成立。

当然，也许有朝一日，我会被很多人打脸，但没办法，先诚实地袒露自己的看法，到时候知道错了再后悔也来得及

1.3 猫咪减肥案例-提出假设

猫咪减肥的ABtest：双独立样本T检验
对比两组数据：运动减肥前90天的体重数据、运动减肥后30天的体重数据
研究变量影响：判断运动减肥是否有效。

对待运动减肥的猫咪案例也是如此，猫咪减肥前后体重的差异，有可能是随机误差，也有可能是运动导致的本质差异 。

没有证据前，我们应该认为它既可能是随机误差，也有可能是本质差异，即提出差异不显著的原假设。
H0 : μ1 = μ2 （减肥前后，体重差异不显著）

另外提出差异显著的备择假设。
H1：μ1 ≠ μ2（减肥前后，体重差异显著）

完成了第一步提出假设后，接下来，我们将进入第二步，计算检验统计量。

2. 计算检验统计量

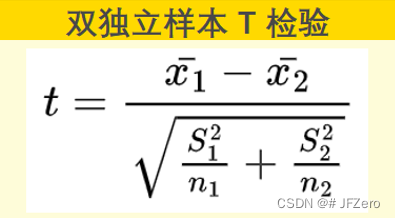
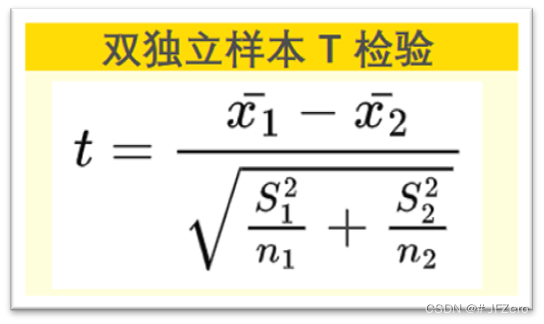
我们知道，猫咪减肥案例是应用双独立样本T检验，因此检验统计量 t 值公式如下：

在进行计算前，为了不糊里糊涂，先来拓展了解检验统计量公式原理。

2.1.1 单样本检验的公式原理

单样本检验，是检验样本是否来自总体，因此是以样本均值与总体均值的差异（即x-μ），对照总体正态，计算检验统计量。

为什么分母部分是$\sqrt{\frac{{\sigma }^2}{n}}$呢！

很纠结，要不要讲呢，讲起来可能真又臭又长，但是不讲，感觉失去了灵魂。
失去灵魂，我所有的笔记，就变为了描绘躯壳，套壳即可用！
但没有灵魂，可不就没意思了嘛！

通常在假设检验中，我们通常都是抽取多个数据进行分析检验（因为抽取单个数据，随机性太大，分析结果不太可靠）。

而抽取多个数据，实际就是抽样。

所有可能的样本均值，实际等于总体均值：例如抽取n=30的样本，穷尽所有n=30的样本组合，这些样本组合的均值最终等于总体均值。

那这些样本均值的方差，是否等于总体方差呢？？？
——这是我非常困惑的！如果能解决这个困惑，想必我会思路更清晰

最终找到：所有样本均值的方差 = $\frac{总体方差}{n}$，证明如下

到这里！！！！！思路异常清晰了！！！！！啊！！！！

我终于可以大声的说，根据【中心极限定理】是可以在总体不服从正态分布的情况下，进行显著性检验的！！！！
天知道，我是一边写，一边才捋顺我之前的困惑！！！！！

我要推翻我之前对于检验统计量公式的任何讲解

首先，显著性检验，是基于样本均值服从正态分布的前提下进行的！
不是基于总体服从正态分布！

检验统计量公式的三座数据基石：
1）所有可能的样本均值，实际等于总体均值
2）所有可能的样本均值方差，实际等于$\frac{总体方差}{n}$
3）中心极限定理：当样本量n较大时，所有可能的样本均值，服从正态分布。

实际上的显著性检验，就是样本均值vs样本均值总体（即所有可能的样本均值组合）的检验。
样本均值总体：根据【基石3-中心极限定理】，明确服从正态分布；
样本均值总体：根据【基石1】，明确 样本均值的总体均值 为 样本的总体均值 μ
样本均值总体：根据【基石2】，明确 样本均值的总体方差 为 样本的总体方差σ² 的$\frac{1}{n}$，即$\frac{{\sigma }^2}{n}$

这里要区分，【样本均值的总体】，与【样本的总体】是不一样的：
-样本均值的总体：由所有可能的样本均值，组合成的总体
-样本的总体：由所有可能的样本数据，组合成的总体

因此，样本均值，服从N(μ，$\frac{{\sigma }^2}{n}$）的样本均值总体的正态分布。

那么，单样本检验：实际就是单个样本均值 vs 总体样本均值的检验。

那么，一般正态分布要计算出概率 P 值，需要转化为标准正态分布，这样就能够解释通了

至此，一切豁然开朗！！！！！！！！！
太开朗了我的天

这里，一定要讲解，标准正态分布与普通正态分布之间的关系！！

重点：标准正态分布与普通正态分布

标准正态分布 N(0,1)，对应的概率密度函数为：

对标准正态分布的概率密度函数进行积分，求出概率 P 值（积分上下限是标准正态分布下的检验统计量）。

因此，普通的正态分布，其实是可以转化为标准正态分布，再进行积分计算出 P 值的（积分上下限是标准正态分布下的检验统计量）。
普通正态分布的概率密度函数如下：

因此，检验统计量的存在，主要是将正态分布中的概率密度函数的 x，换为普通正态分布下求得的检验统计量=均值差/标准差

所以，检验统计量，应该是普通正态分布下的 均值差/标准差，即 $\frac{x-\mu }{\sigma }$，才能根据标准正态分布，求得概率 P 值。

之前，我有个非常巨大的困惑：为什么在 Z\T检验中，检验统计量的公式是 $\frac{x-\mu }{\sigma /\sqrt{n}}$，这样的检验统计量，根本没法按照标准正态分布的概率密度函数求概率 P 啊！

现在，我曾经的困惑终于得到了解释！！！

原因就是，Z\T检验的基础：样本均值，服从N(μ，$\frac{{\sigma }^2}{n}$）的样本均值总体的正态分布。

所以，样本均值总体的正态分布，均值是μ，方差是$\frac{{\sigma }^2}{n}$，那么标准差就是$\frac{\sigma }{\sqrt{n}}$

根据普态转正态的公式： 检验统计量 = $\frac{均值差}{标准差}$=$\frac{x-\mu }{\sigma /\sqrt{n}}$

所以啊！！！！！无论总体是否服从正态分布，只要样本均值，服从正态分布，那就完全可以进行显著性检验辣！！

于是，我忍不住思考，为什么市面上很多显著性检验，要求总体服从正态分布呢？

其实，总体服从正态分布，可以弥补中心极限定理的缺陷：

• 中心极限定理：当样本量足够大（统计研究发现n≥30时，样本均值服从正态分布），如果总体偏态严重，那么n需要更大一些。
  
  中心极限定理的缺陷在于，要求样本量足够大的情况，但当样本量不够大，样本均值就不服从正态分布了吗？

不，不是的！

当总体服从正态分布时，那么总体中的每个数据（即n=1的样本），本身就服从正态分布，样本均值=数据值，也服从正态总体；
👉由此可推测，样本量n比较小的时候，只要总体服从正态分布，那么样本均值也是会服从正态分布的。

那么，要进行正态分布下的Z\T检验，只需要符合以下两种情况：

• 1）总体服从正态分布
• 2）如果样本量较大(通常是n≥30）——【中心极限定理】

到目前为止，都还是在推测中…仔细想想，不无道理吧
不过无所谓，等到哪天，万一又有新的认知发现呢！

检验统计量公式原理总结

• 正态性的显著性检验本质：样本均值，服从正态分布（即，样本均值总体）
  ①如果样本的总体，均值为μ，方差为σ²
  ②那么样本均值的总体，均值为μ，方差为$\frac{{\sigma }^2}{n}$【可证】
  👉因此，当样本均值，服从正态分布时，样本均值的正态总体为 N（μ，$\frac{{\sigma }^2}{n}$）
• 检验统计量的本质：$\frac{均值差}{标准差}$
  ①将普态转为标态，可证得统计检验量本质
  👉因此，将样本均值的正态分布 N（μ，$\frac{{\sigma }^2}{n}$）（普态），转为标态。
  即为检验统计量=$\frac{均值差}{标准差}$=$\frac{x-\mu }{\sigma /\sqrt{n}}$，再根据标态求积分，可得概率 P 值。

单样本 Z 检验

检验统计量 Z 值：z = $\frac{x^{-}-\mu }{\sigma /\sqrt{n}}$
σ 是总体的标准差。

单样本 T 检验

实际有时是无法获取到总体的标准差，则可用样本标准差来代替总体标准差，样本代替总体的检验，即为 T 检验。
但用样本代替总体，需要给一点宽松自由度。
自由度为 n-1

检验统计量 T 值：t = $\frac{x-\mu }{S/\sqrt{n}}$，自由度为 n-1

2.1.2 双独立样本检验的公式原理

双样本检验，则与单样本不同：
样本1的均值服从样本1均值的正态总体，样本2的均值服从样本2均值的正态总体
👉则样本1均值-样本2均值 ，也服从正态

N（μ1，$\frac{\sigma 1^2}{n1}$）-N（μ2，$\frac{\sigma 2^2}{n2}$）~N( μ1-μ2，$\frac{\sigma 1^2}{n1}$+$\frac{\sigma 2^2}{n2}$-2cov(x1，x2) )

👆这是正态的加减性质（cov(x1，x2)为协方差，即相关性系数）

如果两个样本是独立的，则相关系数为0，则
N（μ1，$\frac{\sigma 1^2}{n1}$）-N（μ2，$\frac{\sigma 2^2}{n2}$）~N( μ1-μ2，$\frac{\sigma 1^2}{n1}$+$\frac{\sigma 2^2}{n2}$ )

因此，在双独立样本T检验中，其实以样本1均值-样本2均值的差值，也服从正态分布的前提下，进行**差值均值（x1-x2)与差值均值的总体均值(μ1-μ2）**的检验。

最终，双独立样本的检验，本质上也是化作了单样本检验：
即均值之差（样本）vs差值的均值正态总体（总体）检验。

就是把样本1均值-样本2均值的差值作为一个样本，与差值的均值正态总体进行检验——即单样本检验。

由于在原假设中，我们假设μ1=μ2，因此μ1-μ2=0

所以最终双独立样本检验的t值（或z值，差异不大），变为了如下：

双独立样本 T 检验

实际有时是无法获取到总体的标准差，则可用样本标准差来代替总体标准差，样本代替总体的检验，即为 T 检验。
但用样本代替总体，需要给一点宽松自由度。
如果双样本方差齐性（F检验）：自由度为 n1-1+n2-1=n1+n2-2
如果双样本方差不齐性（F检验）：自由度为

3. 计算概率 P 值

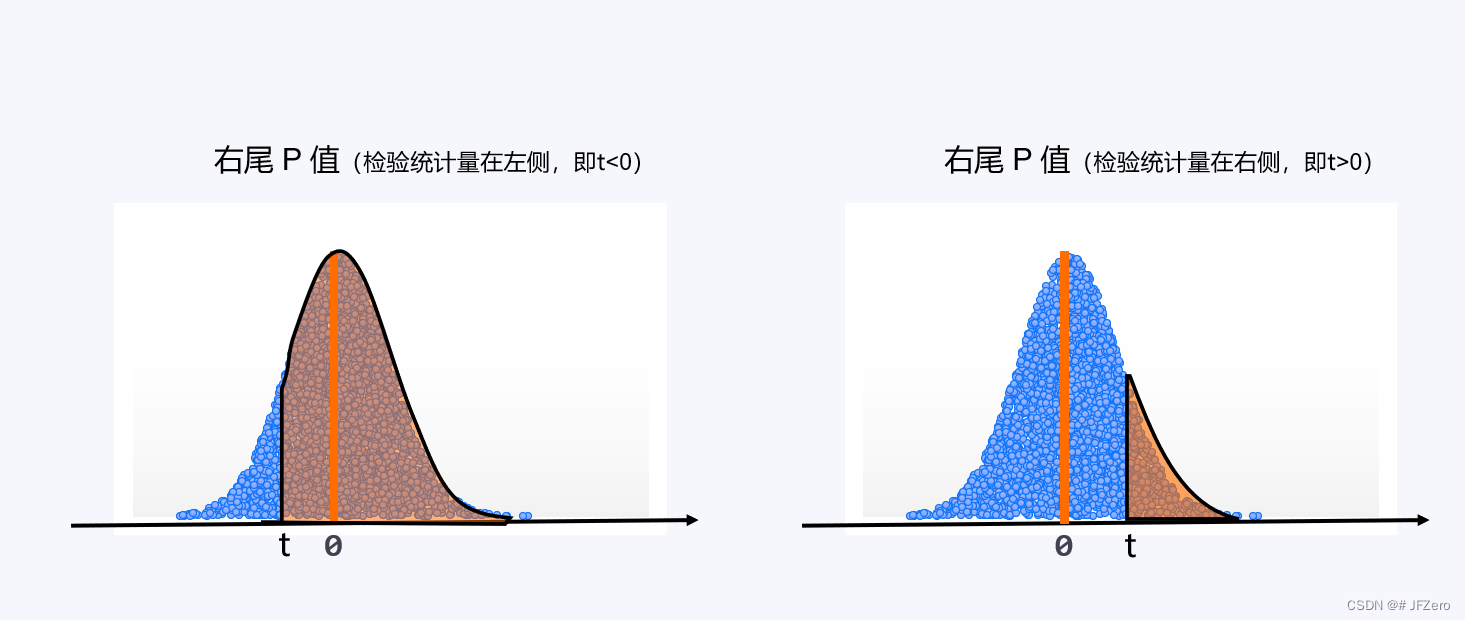
概率 P 值，分为左尾 P 值、右尾 P 值、双尾 P 值。

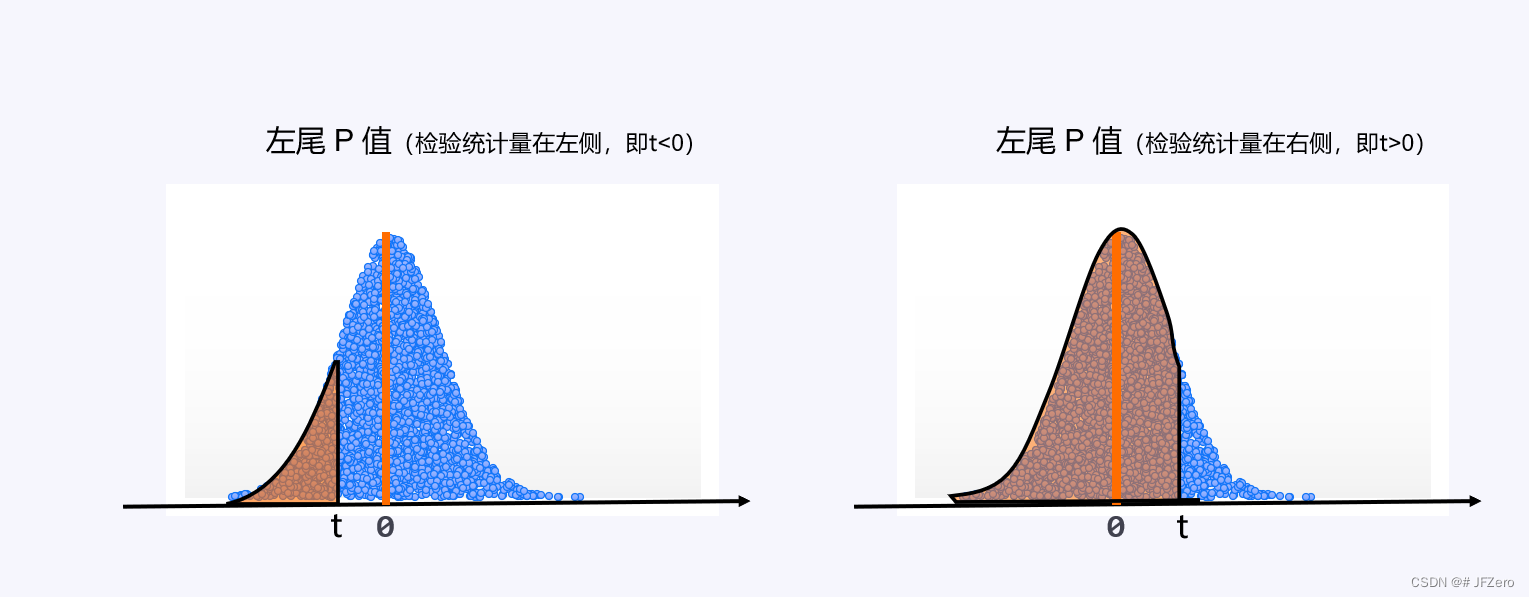
3.1 左尾P值

左尾 P 1值：是根据标准正态分布的概率密度函数，下限为 -∞，上限为检验统计量，积分而得。
T检验的左尾 P 值Excel函数：T.DIST(检验统计量,自由度,TRUE)

但在实际应用中，一般是用于检验谁比谁小的情况下用的。

例如：检验算法调整后，出错率比之前的出错率要小。

那么配合的检验统计量就是：（现在的出错率-之前的出错率）/标准差

如果现在出错率<之前出错率，那么检验统计量<0，则计算出的就是上边的左图状态
如果现在出错率>之前出错率，那么检验统计量>0，则计算出的就是上边的右图状态

3.2 右尾P值

右尾 P 值 = 1-左尾 P 值
T检验的右尾 P 值Excel函数：T.DIST.RT(检验统计量,自由度)=1-T.DIST(检验统计量,自由度,TRUE)

但在实际应用中，一般是用于检验谁比谁大的情况下用的。

例如：检验策略调整后，销售额比之前的销售额要大。
那么配合的检验统计量就是：（现在的销售额-之前的销售额）/标准差

如果现在销售额<之前销售额，那么检验统计量<0，则计算出的就是上边的左图状态
如果现在销售额>之前销售额，那么检验统计量>0，则计算出的就是上边的右图状态

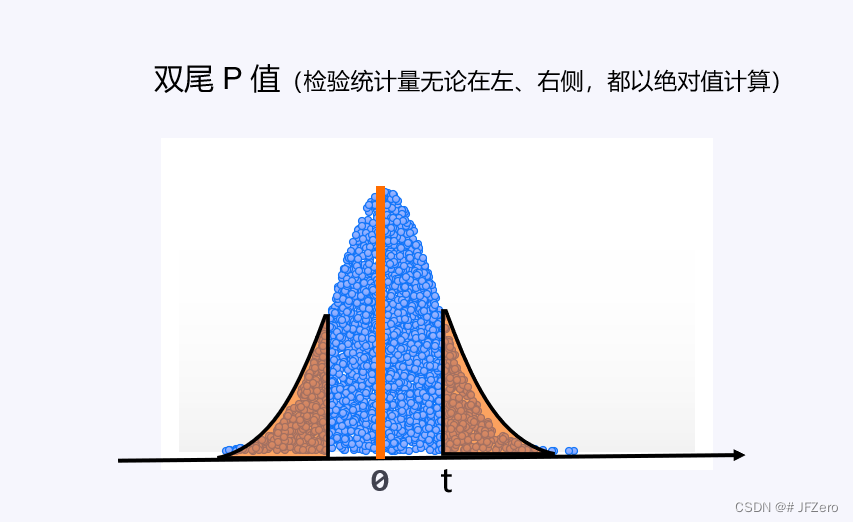
3.3 左尾P值

双尾 P 值：检验统计量的绝对值，自由度
T检验的双尾 P 值Excel函数：T.DIST.2T( ABS(检验统计量),自由度 )

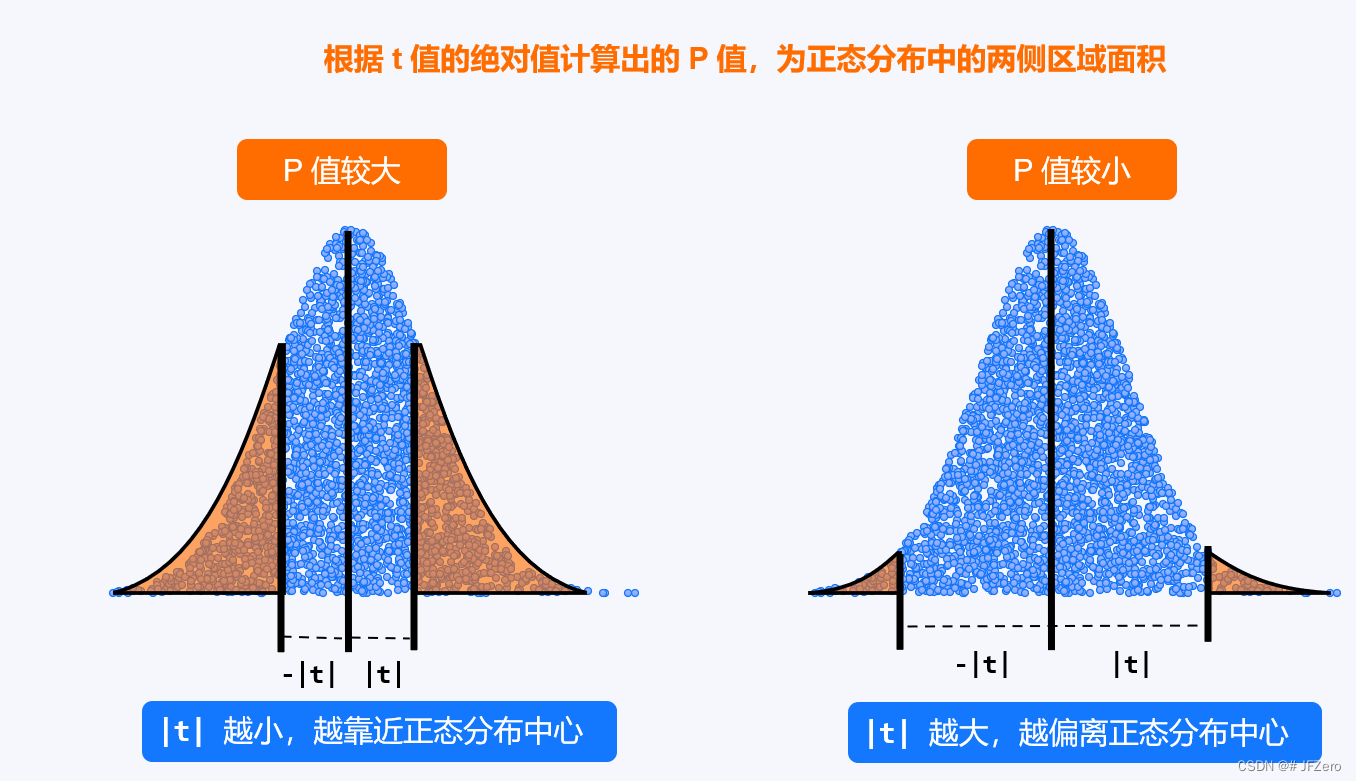
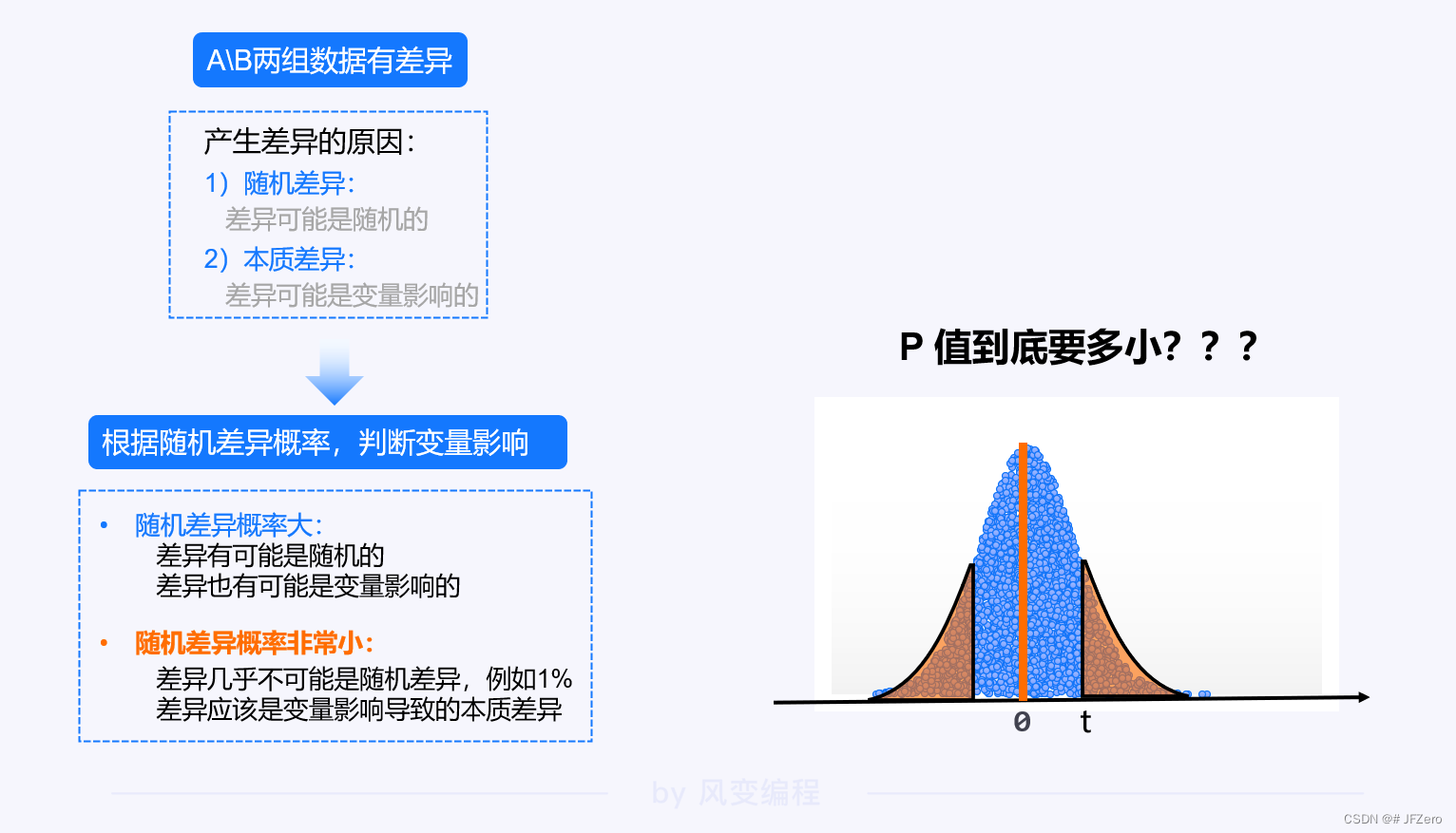
我们知道，概率 P 值，实际就是随机差异概率，随机差异概率到底要多小，才能认为差异不可能是随机差异！

这就需要一个界限，才能衡量。

虽然，我个人反对按照某一个固定的界限，来给世间万物划分三六九等
但无奈的是，现实通常如此，只有标准才尽可能公平公正

所以，人为地给 P 值设置一个界限，就是规定显著性水平 α

4. 规定显著性水平α

统计学上，通常将 α 设置为0.05，它意味着无论是左尾、右尾、双尾的P值，都是以α为界限。

如果 P 值<α：则认定 P 值非常非常小，差异几乎不可能是随机差异
如果 P 值>α：则认定 P 值较大，差异有可能是随机差异，也有可能是本质差异

以双尾检测为例

4.1 左尾检测

左尾检测时，α=0.05，相当于检验统计量为-1.64时，计算出的左尾 P 值

可以用检验统计量与-1.64进行比较，也可直接得出差异是否显著

4.2 右尾检测

右尾检测时，α=0.05，相当于检验统计量为1.64时，计算出的右尾 P 值

可以用检验统计量与-1.64进行比较，也可直接得出差异是否显著

4.3 双尾检测

α 设置为 0.05，表示检验统计量为 ±1.96 时，计算出的双尾 P 值。

可以用检验统计量与 1.96 进行比较，也可直接得出差异是否显著

α 通常也会设置的更小，这样检验要求就更严格！

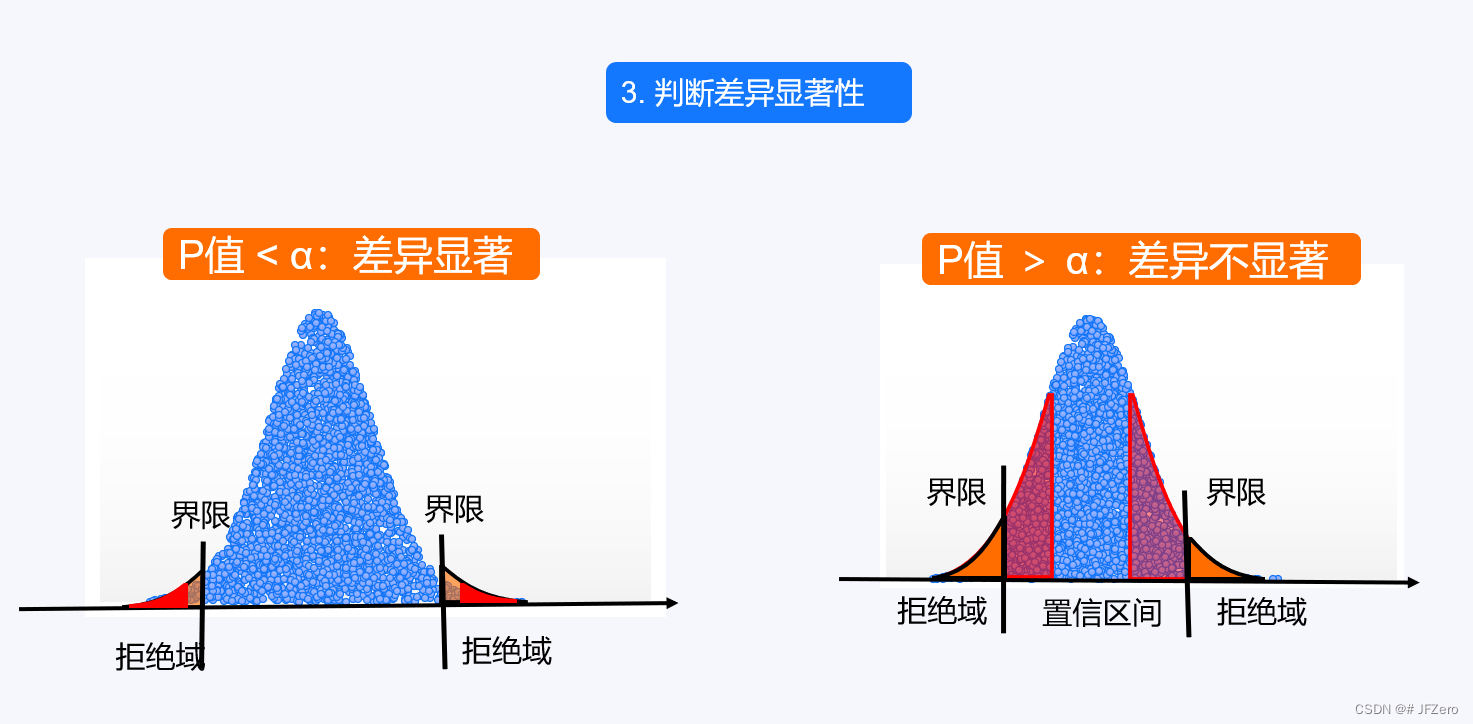
5. 判断差异显著性

概率比较法

用 P 值与α 比较

• P 值<α：随机差异概率较大→差异有可能是随机差异，也可能是本质差异，差异不显著

• P 值>α：随机差异概率非常小→差异几乎不可能是随机差异，应该是本质差异，差异显著

区间比较法

用P值检验统计量与α 所对应的检验统计量比较

今天的文章假设检验的流程及步骤_假设检验包括哪些类型分享到此就结束了，感谢您的阅读。