泰勒级数求sin 程序_泰勒级数的系数公式「建议收藏」

前情提要 R语言微积分

• 极限
• π , e , γ \pi, e, \gamma π,e,γ
• 洛必达法则
• 连续性和导数
• 数值导数
• 差商与牛顿插值
• 方向导数

泰勒级数是如何被发现的

如果我是泰勒，我会把思考的起点建立在这样的一个等式上

$$f^{(n)}(x)=P^{(n)}(x)$$

即如果想用一个多项式函数$P$来对$f(x)$进行逼近，则要求这个多项式的任意阶导数均与$f(x)$相等。

这个条件过于严格，简单起见，不妨添加一个最接近的点$x_0$，要求

$$f^{(n)}(x_0)=P^{(n)}(x_0)$$

则多项式函数可以十分便利地写为

$$P(x)=\sum _{i=0}^N{a}_i(x-x_0{)}^i$$

从而当$i<n$时，有$((x-x_0{)}^i{)}^{(n)}=0$，故而

$$P^{(n)}(x)=\sum _{i=n}^N(x-x_0{)}^{i-n}\frac{1}{n!}$$

当$x=x_0$时，有

$$\underset{x\to x_0}{\lim }{P}^{(n)}(x_0)=n!a_n+n!\sum _{i=n+1}^N(x-x_0{)}^{N-i}=\frac{a_n}{n!}$$

由于$f(x)=P(x)$，从而，当$x\to x_0$时，

$$a_n=\frac{f^{(n)}(x_0)}{n!}$$

就此得出了$f(x)$的多项式拟合表达式

$$f(x)=\sum _{i=0}\frac{f^{(i)}(x_0)}{i!}(x-x_0{)}^i$$

用图像理解Taylor级数的逼近过程

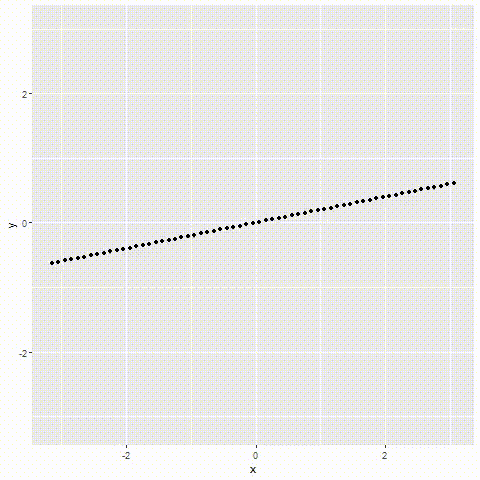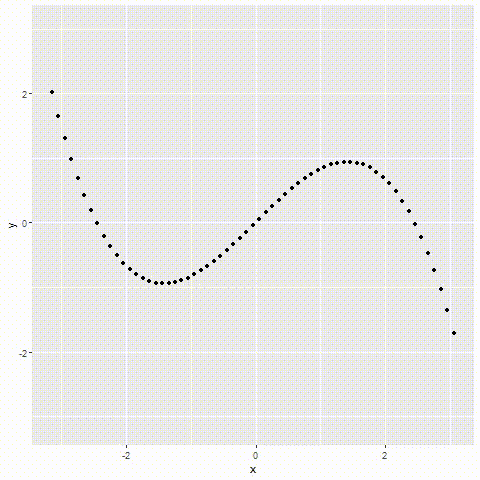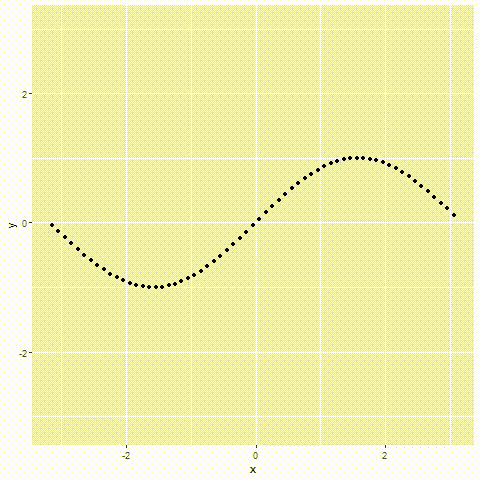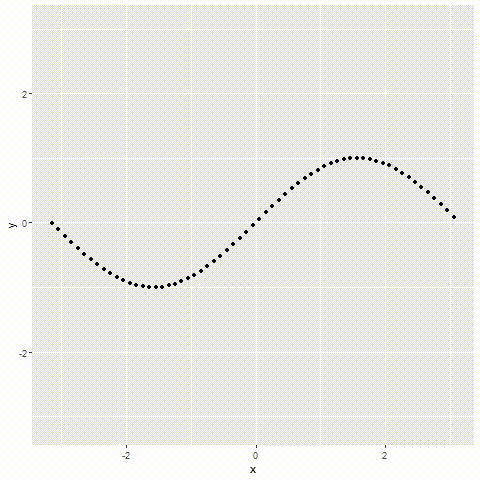
那么接下来我们直观地感受一下Taylor级数时如何逐渐逼近某个函数的。简单起见，在此选择$\sin x$作为被拟合的函数。

library(ggplot2)
library(gganimate)
library(av)
library(tibble)

x = seq(-pi,pi,0.1)
n = length(x)

xs = rep(x,11)
ys = rep(sin(0),n)
ts = rep(0,n)

for(i in 1:10){ 
   
    y <- if(i%%2==0) 0 else 1
    if((i-1)%%4>1)
        y = -y
    y = y/factorial(i)*x^i
    m = length(ys)
    y = y+ys[(m-n+1):m]
    
    ys = c(ys,y)
    ts = c(ts,rep(i,n))
}
data<-tibble(x=xs,y=ys,t=ts)
ggplot(data,aes(x,y))+geom_point()+transition_time(t)+ease_aes('linear')

如下图所示，随着阶数的不断增多，Taylor级数对三角函数的形式越来越适应，最后大约在第5次之后，其变化就已经微不可察了，这就是多项式逼近的强大之处。

今天的文章泰勒级数求sin 程序_泰勒级数的系数公式「建议收藏」分享到此就结束了，感谢您的阅读。