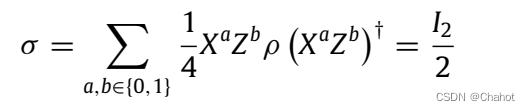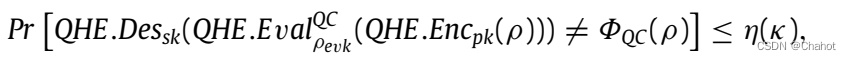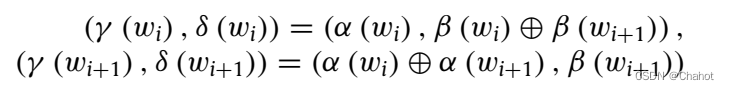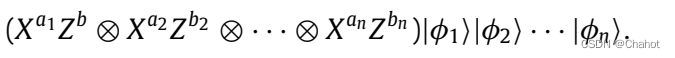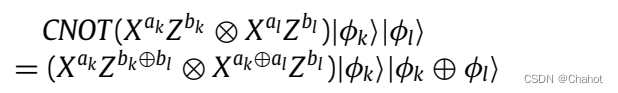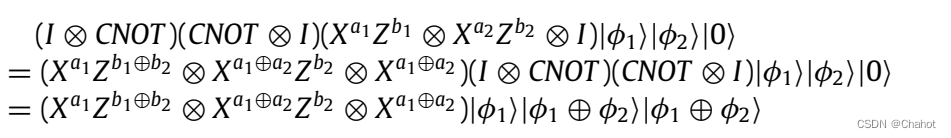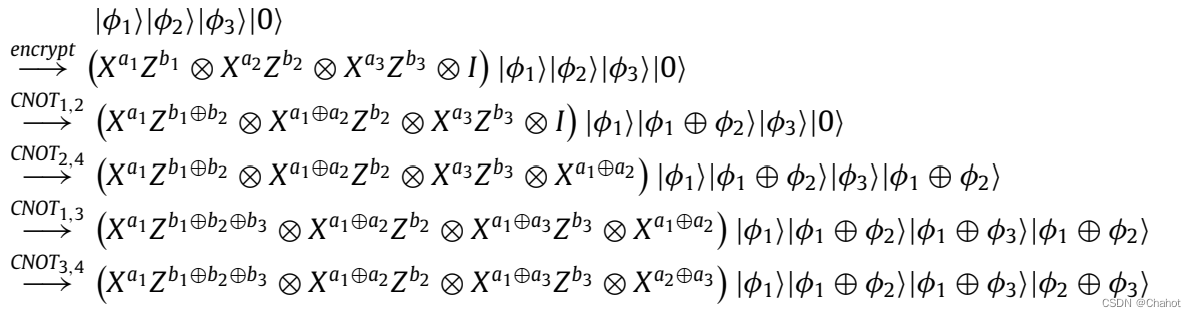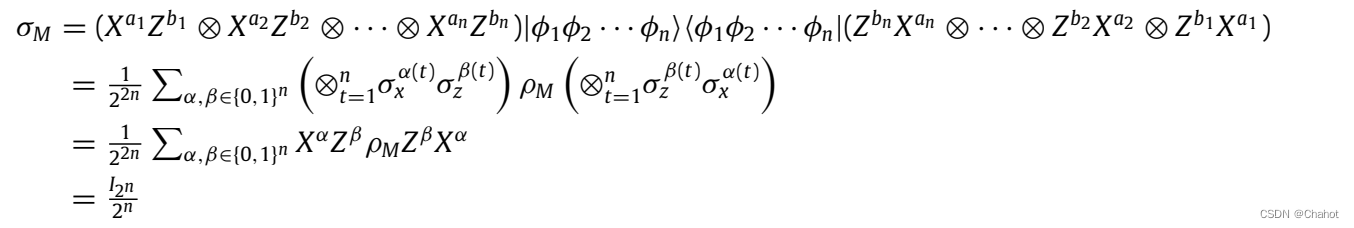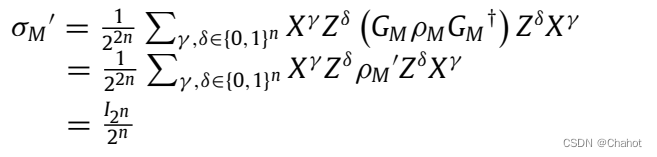基于量子同态加密的改进多方量子私有比较

背景

量子密码学作为保证计算安全和数据安全的重要手段，最早由Wiesner提出，利用量子的特性来保护信息安全。量子物理中的量子不可克隆定理和海森堡测不确定原理保证了量子密码的安全性。与许多经典密码方案相比，它不需要依赖于一些困难的数学问题。量子密码学的最大优势在于其无条件的安全性和防窃听的可探测性。直到20世纪80年代，Bennett和Brassard才提出了著名的量子密钥分发(QKD)协议，简称BB84协议。随后，一些量子密码协议被广泛研究，包括量子秘密共享、量子私有查询、量子盲计算、量子同态加密和量子私有比较。
量子同态加密(QHE)的优点在于它不仅可以保护用户的私有数据不被泄露，而且可以在远程服务器上对加密后的数据进行安全的量子计算。2012年和2014年，从可行实验的角度出发，Rohde等和Fisher等分别利用量子行走和线性光学实验提出了量子计算方案。2013年，Liang给出了QHE和量子完全同态加密(QFHE)的概念和框架。然后，Liang构造了一个具有完美安全性的交互式两方QHE方案。然而，2014年Yu等发现，为了满足非交互性，任何具有信息理论上安全的QFHE方案必然会占用指数级大小的存储空间。2015年QFHE研究取得进展。Broadbent and Jeffery (BJ15)给出了QHE和QFHE的正式定义，并提出了两种非clifford栅极数量有限的QHE方案。此外，在Tham等人提出的方案中，BJ15也被实验证明是可行的。2016年，Dulek等将有限非clifford栅极电路扩展到任意多项式大小的电路。2017年，Alagic等人构造了一个可以验证密文同态评价的分层QHE方案。然后，Mahadev[14]使用经典的水平全同态加密方案实现了量子电路的评估。上述方案基于经典同态加密和量子一次性填充，以及利用群论思想和纠错码、门传送等量子技术的QHE方案，但仅限于双方的研究。近年来，越来越多的研究将QHE方案与其他量子密码协议相结合，在保证数据安全的同时完成量子计算任务。2019年，Chen等创新性地提出了一种可变数量评估者的QHE方案，该方案将QHE与多方量子秘密共享相结合，实现了两个及两个以上诚实评估者有序进行同态评估的方案。这使得QHE方案在应用场景上有了更多的可能性。随后，也出现了基于QHE的密文检索方案、量子求和方案和使用量子同态信息认证技术的安全量子网络编码方案，这些方案在保证私有数据安全的同时完成了各种量子计算任务。
在多方量子计算任务中存在这样一种场景，即相互不信任的多个用户希望进行安全的多方计算，并在不泄露其私有信息的情况下获得结果。量子私有比较(QPC)作为安全多方计算的一个重要分支，为解决上述问题提供了有效的方法。它允许所有参与者同时公平地获得隐私比较结果，并且在此过程中，每个参与者的隐私信息都是保密的，不会被其他参与者、第三方或外部攻击者窃取。双方QPC协议最早由Yang和Wen于2009年研究。随后，陆续提出了基于不同量子资源的双方QPC协议，如单光子，EPR对、GHZ态和W态、χ型态、簇态等。在后续的研究中，多方量子私有比较(MQPC)协议是在双方量子私有比较协议基础研究的基础上取得的成果。在半诚实第三方(TP)的帮助下，提出了基于不同量子资源的MQPC协议。其中，半诚实的TP一方面忠实地执行协议，另一方面可能试图利用被动攻击窃取参与者的隐私信息。后续工作广泛研究了几乎不诚实的TP，其中参与者也可以部分信任TP，但TP会主动执行对协议的任何攻击，除非与任意参与者或其他TP勾结。2015年，Huang等利用几乎不诚实的TP，提出了第一个MQPC协议，安全高效地比较了多个用户的保密信息。之后，他们引入了第二个几乎不诚实的TP，以防止比较结果被伪造。当参与者是陌生人时，该协议可以安全地执行。然而，GHZ态的制备和两轮诱饵光子的探测在实验上增加了协议的技术难度。如果发现不正确的计算结果，将导致协议异常退出，从而导致量子资源的高消耗问题。也无法抵御恶意第三方和参与者的串通攻击。因此，我们将利用同态性，即可以对加密后的数据进行任意量子计算，并在解密后得到我们想对原始数据执行的求值计算结果，从而提高了协议的安全性。同时，我们可以在不检测诱饵光子的情况下只制备单粒子态来完成私下比较的任务，这大大降低了资源消耗和实验实现的难度。
本文提出了一种基于QHE的MQPC协议。最初，该协议可以委托给几乎不诚实的TP执行，其中TP将忠实地执行同态计算，但将采取任何可能的方法窃取参与者的隐私信息。其次，引入可信密钥中心进行密钥的生成和更新，同时保证比较结果的诚实发布;最后，在IBM Q体验平台上进行了仿真，验证了协议的正确性，得到的统计结果表明了协议的有效性。此外，我们的协议在安全性方面也具有良好的性能。

基础知识

QOTP

量子密码学的安全性依赖于量子力学的特性，可以实现信息理论上的安全。在量子数据设置中，使用量子一次性密匙(QOTP)加密私有信息。对于量子态ρ，随机选择a, b∈{0,1}作为pad的密钥。利用泡利算子对量子信息态进行加密，得到完全混合态的密文σ。每次对量子态进行加密时，都会随机生成一个新的泡利密钥。只有拥有解密密钥的人才能对密文进行解密，从而获得有效的信息。因此，攻击者拦截整个密文是没有意义的。信息以完全混合的状态隐藏，安全性得到保证。

量子同态加密

1. 密钥生成。QHE注册机$(1^{\kappa })\to (pk,sk，{\rho }_{evk})$，其中κ∈N为安全参数。pk和sk都是经典密钥，分别用于加密和解密量子信息。作为评估密钥，ρ_evk可以是一个量子态，在对加密数据进行量子电路评估时将消耗该量子态。
2. 加密。$QHE.En{c}_{pk}(\rho )\to \sigma$。使用公钥pk将量子明文ρ加密为密文σ。
3. 评估。$QHE.Eva{l}_{{\rho }_{evk}}^{QC}(\sigma )\to \sigma \prime$。量子评估电路QC应用于量子密文σ，即在不解密的情况下完成对加密数据的评估操作。生成了一个新的量子密文状态σ ‘。
4. 解密。 $QHE.De{c}_{sk}(\sigma \prime )\to \rho \prime$。用私钥sk对密文σ′进行解密，得到明文状态ρ′，这是将量子评估电路应用于初始明文ρ的结果。

对于任意量子电路QC和输入量子明文ρ，若存在可忽略的函数η，则满足以下条件

密钥更新策略

在QHE方案的建立中，具有量子信息的客户端需要将计算和处理委托给远程服务器。量子信息将由QOTP根据经典加密密钥$pk=(\alpha ，\beta )，(\alpha ，\beta \in {0,1}^n)$进行加密或解密，该密钥使用泡利算子改变输入量子比特，即$X^{\alpha }{Z}^{\beta }$，其中$X^{\alpha }={\otimes }_{t=1}^n{\sigma }_x^{\alpha (t)}$,$Z^{\beta }={\otimes }_{t=1}^n{\sigma }_z^{\beta (t)}$ 。$X^{\alpha }$对应于对n位字符串α中给定位置的第t个量子位执行${\sigma }_x$, $Z^{\beta }$也类似。那么，解密密钥$sk=(\gamma ，\delta )，(\gamma ，\delta \in {[0,1]}^n)$在对通用门集进行同态求值时需要同步刷新，密钥更新规则将在这里进行回顾。
该协议的同态求值仅针对Clifford群的两个量子位CNOT门,假设一个CNOT门作用于两条量子线路，分别是控制线wi和目标线wi+1，键更新规则如下。

基于QHE的MQPC协议

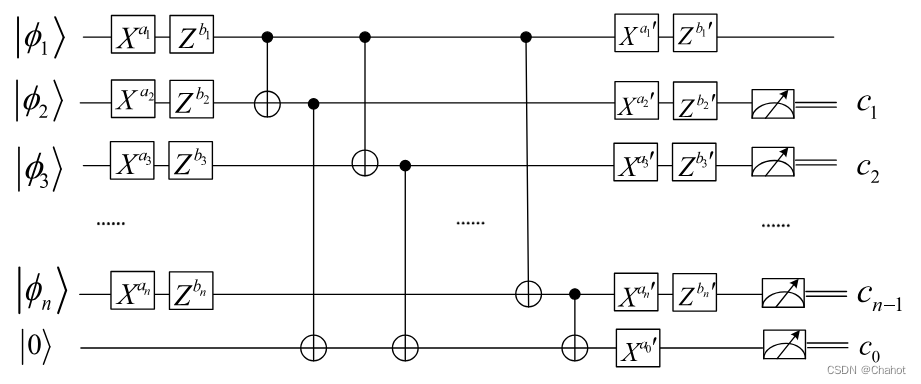
在本节中，我们将提出一种基于QHE的改进的MQPC协议，它允许参与者完成加密信息位的比较。TP是一个计算能力很强但几乎不诚实的服务器，它负责对加密数据进行比较，而一个可信的密钥中心(表示为Charlie)负责分发和更新密钥，对评估的数据进行解密，并诚实地宣布比较结果。假设有n个参与者，用Pi(i = 1,2，…)表示。， n)，他们想要比较他们的m位私有信息Mi j (i = 1,2，…)， n, j = 1,2，…， m)是平等的，但不愿意透露隐私信息的内容。因此，我们引入了一个QHE方案，允许服务器对加密数据执行计算。解密后，得到的计算结果是对原始数据的期望，可以诚实地向所有参与者公布。此外，还可以通过独立于测量设备的量子密钥分发(MDI-QKD)来实现密钥的安全分发。接下来，我们将分步骤描述提出的MQPC协议，并详细给出图1中协议的量子电路。

步骤1:密钥生成阶段。法定沟通方是Pi和Charlie。它们分别通过使用可信的准备源随机地准备集合{|0⟩，|1⟩，|+⟩，|−⟩}中的一个量子态。然后他们将准备好的量子态发送给TP。一个贝尔态测量由TP对每一对量子态$|{\psi }_{pi}⟩|{\psi }_{ci}⟩$进行，并且测量结果被返回。Pi和Charlie在经典认证通道上发布与准备好的量子态相对应的基信息。根据TP的测量结果$|{\Phi }^{\pm }{⟩}_{pici}，|{\Psi }^{\pm }{⟩}_{pici}$，保留相同制备基的量子位，此时获得的密钥是筛选后的密钥。然后公布经过筛选的部分密钥，并通过纠错和隐私放大等后处理检查错误率。如果误码率低于阈值，则说明没有窃听者，通道安全。他们也同意编码规则是|0⟩，|+⟩→“0”和|1⟩，|−⟩→“1”，因此Pi和Charlie得到相同的安全密钥，表示为ek_i = (ai, bi)，其中ai, bi∈{0,1}。

步骤2：加密阶段。在步骤1中随机生成的密钥ek_i被用作量子一次性加密密钥。每个参与者对要比较的私有信息的第一个比特进行加密，并将其发送给TP。TP接收到的加密状态如下:

步骤3： 同态评估阶段。基于QHE方案的同态特性，在接收到加密状态后，TP完成对任意两个参与者$P_k(k=1,2，\dots n)$和$P_l(l=1,2，\dots ，n)$，其中k≠l，所拥有的加密状态的评估。使用Pk的粒子作为控制位，使用Pl的粒子作为目标位来执行CNOT操作，并将评估结果发送给Charlie。

当参与者的数量n≥3时，将需要引入一个辅助粒子|0⟩，并且TP根据发送加密状态的顺序执行一系列操作。首先，将第一个参与者的加密状态作为控制位，将第二个参与者的加密状态作为应用CNOT门的目标位。这个目标位然后作为控制位工作，并且辅助粒子|0⟩作为目标位工作以应用CNOT门。然后，再次将第一个参与者的加密状态作为控制位，将第三个要比较的参与者的加密状态作为目标位，重复上述操作。直到除第一个参与者之外的所有参与者的加密状态被用作目标位和控制位，以执行相应的CNOT操作。比较结束，结果发送给Charlie。

步骤4： 揭秘阶段。在任意两方的设置中，Charlie更新加密密钥以获得解密密钥，其形式为$d{k}_i=(a_k^{\prime },b_k^{\prime },a_l^{\prime },b_l^{\prime })$。密钥变换为$e{k}_k=(a_k,b_k)，e{k}_l=(a_l,b_l)\stackrel{update}{\to }d{k}_i=(a_k^{\prime },b_k^{\prime },a_l^{\prime },b_l^{\prime })=(a_k,b_k\oplus b_l,a_k\oplus a_l,b_l)$，利用dk_i对求出的量子态进行解密。粒子被测量的结果为|0⟩时，秘密信息被声明为相同。否则，保密信息是不同的。
当参与者的数目n≥3时，除了一直处于控制位置的第一个参与者所拥有的粒子外，所有粒子，包括辅助粒子，都在基|0⟩，|1⟩中测量。将n个测量结果ci(i = 0,1，…)相加的结果。， n−1)记为Rj(j = 1,2，…)如果Rj = 0，则Charlie宣布多个参与者持有的秘钥位不同，协议结束。否则，协议将继续比较多个参与者的下一位私有数据，直到比较第m位。如果${\sum }_{j=1}^{m}Rj=0$，则通告这些参与者的私有数据是相同的。整个过程如上图所示。
正如上述协议所介绍的，通过实现我们的比较协议，可以对陌生环境中任意数量的参与者之间的隐私数据进行安全比较。参与者制备了没有诱饵光子检测的单光子，减少了量子资源的消耗，使协议更容易在实验条件下实现。同时，量子同态加密的优势和可信密钥中心的作用使TP无法访问任何隐私数据，保证了隐私数据的完美安全性和比对结果的真实发布。可以看出，几乎不诚实但计算能力较强的第三方服务器适合于QHE方案的设置，该方案可以在不解密的情况下完成加密数据的量子同态计算，实现多参与者的隐私比较任务。它不仅有效地探索了QHE方案的多方应用场景，而且解决了多个互不信任参与者之间的安全委托计算问题。

精确度分析

在本节中，我们将分析并验证上述协议的正确性。在IBM Q实验平台上对该协议进行了仿真，结果证明了该协议的有效性和可行性。在不失一般性的前提下，我们以n = 2和n = 3的参与者人数为例来证明下面的正确性。首先，当n = 2时，即有两个参与者P1和P2来比较量子隐私。基于QHE的MQPC协议中的步骤3到步骤4可以表示为:

通过上述协议，解密后得到的结果为$|{\varphi }_1\oplus {\varphi }_2⟩$。如果辅助粒子的测量结果为|1⟩，则宣布秘密信息不同，协议将终止。否则，直到两个参与者的m位被比较并且所有测量结果都是|0⟩，两个参与者的秘密信息是相同的。可以看出，在我们的协议中，n = 2是一个特例。只有通过测量辅助粒子，才能得到两个参与者拥有的隐私数据的比较结果。

接下来，当n = 3时，有三个参与者来比较量子隐私。步骤2到步骤4的过程可以表示为下式。

因此，一旦执行多方协议，计算和解密后的量子态将变为|φ1⟩|φ1⊕φ2⟩|φ1⊕φ3⟩|φ2⊕φ3⟩。除了仅作为控制位的粒子外，其他粒子的测量结果之和将得到三个参与者持有的比特隐私数据的比较结果，即R1 = c1 + c2 + c0 = (φ1⊕φ2) + (φ1⊕φ3) + (φ2⊕φ3)。由这个方程，我们的协议不仅可以得到三方持有的原始隐私数据的比较结果，也可以得到任意两方的比较结果。由此验证了我们协议中n = 2和n = 3的正确性。
最后，利用IBM Q实验平台对我们的协议进行了仿真，泡利密钥的参数设置如下。(1)设n = 2, a1 = 1, b1 = 1, a2 = 1, b2 = 1，则对应的解密密钥为a ’ 1 = 1, b ’ 1 = 0, a ’ 2 = 0, b ’ 2 = 1, a0 = a1⊕a2 = 0。(2)设n = 3, a1 = 1, b1 = 1, a2 = 1, b2 = 0, a3 = 0, b3 = 1，则对应的解密密钥为a ’ 1 = 1, b ’ 1 = 0, a ’ 2 = 0, b ’ 2 = 0, a ’ 3 = 1, b ’ 3 = 1, a0 = a2⊕a3 = 1。

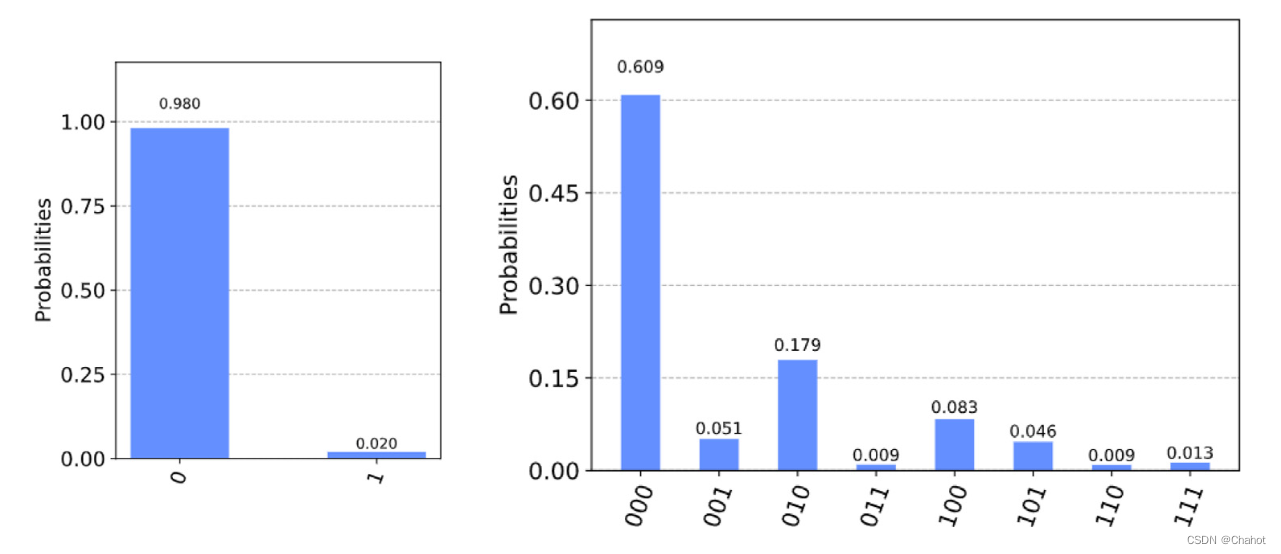
为了运行实验，我们在两种情况下使用代码实现相应的电路，并且要比较的量子态都是|0⟩，如上图所示。在模拟过程中，我们加载IBM帐户，并选择最不繁忙的后端ibmq_vigo和ibmqx2分别执行上述两个电路。情形(1)的测量结果为0，即q0与q1相等，即0⊕0 = 0。在式(2)中，q1、q2、q3的测量结果为000，即q0 = q1、q1 = q2、q2 = q3、q0 = q1 = q2 = q3。因此，所提出协议的仿真电路能够得到正确的比较结果。模拟的镜头数设置为2048。电路测量后的概率统计结果如下图所示。

与模拟电路的计算结果相比，在真实量子器件上的实验实现会有一定的误差。在第一种情况下获得正确测量结果的概率为98%，在第二种情况下获得正确测量结果的概率为60.9%。可以发现，在统计结果中，得到正确结果的概率是最高的。产生误差的主要原因是真实的量子器件会受到噪声的影响，量子门不能完美地工作，从而导致门误差。这些错误可以通过量子纠错码来解决，但这不是本文的重点。综上所述，虽然仿真运行中会出现一些错误，但可以验证基于QHE的两方和三方QPC协议的正确性和有效性。

安全性分析

外部攻击

在提出的MQPC协议中，一方面利用MDI-QKD来解决第三方测量设备不完善造成的安全漏洞，从而保证密钥的安全性。另一方面，我们的协议的主要优点是将QHE的性质转向账户化，使隐私信息的完美安全性得到了很好的保证，可以防止原有隐私信息的泄露。接下来，我们将分析协议的不同阶段，以证明我们的协议可以抵御外部攻击。在密钥生成阶段，安全性的保证依赖于MDI-QKD协议，该协议被严格证明是安全的，不受窃听者Eve的任何攻击。当Eve截获TP发送的Bell测量结果时，假设测量结果为$|{\Phi }^{+}{⟩}_{pici}$，并且根据$|{\Phi }^{+}{⟩}_{pici}$=1/√2( |00⟩+|11⟩ ) = 1/√2(|++⟩+|−−⟩),Eve只能得到pi和Charlie制备的量子态是相同的，但不能确定量子态的制备基是在X基还是Z基。而在后期处理之后，密钥的随机性使得Eve能够获得的信息量几乎为零。同时，随着时间的推移，密钥的规则是不可追溯的，因此夏娃无法推断密钥的内容。
对于其他阶段的外部攻击，与以往的多方QPC协议不同，我们的协议利用了QHE方案中的同态评估。协议中所有想要比较隐私信息的参与者只能自己访问原始隐私数据。他们无权访问其他参与者的数据。即使几乎不诚实的TP或在传输过程中存在窃听者，他们也无法通过拦截加密数据和评估数据来窃取隐私数据的内容。我们的协议可以保证隐私数据的完美安全。
证明： 在该协议中，在将隐私数据传输到TP之前，每个参与者将使用QOTP对其进行加密。QOTP是一种非对称量子加密技术，每次使用不同的随机密钥。它使加密的数据处于完全混合的状态$I_{2n}/2^n$。设ρM为纯输入，${\sigma }_M$为使用QOTP对${\rho }_M$进行加密，即泡利算子$X^{\alpha }{Z}^{\beta }(\alpha ，\beta \in {[0,1]}^n)$，其中$X^{\alpha }={\otimes }_{t=1}^n{\sigma }_x^{\alpha (t)}$,$Z^{\beta }={\otimes }_{t=1}^n{\sigma }_z^{\beta (t)}$。因此，可得式:

换句话说，TP在不知道每个参与者的具体私有信息的情况下，只能接收到加密的量子态$I_{2n}/2^n$。即使有一个Eve，在传输过程中截取加密的数据并获得一些参与者的完整量子态$X^{a_i}{Z}^{b_i}|{\varphi }_i⟩$，他也无法在不知道密钥的情况下知道具体的隐私数据。
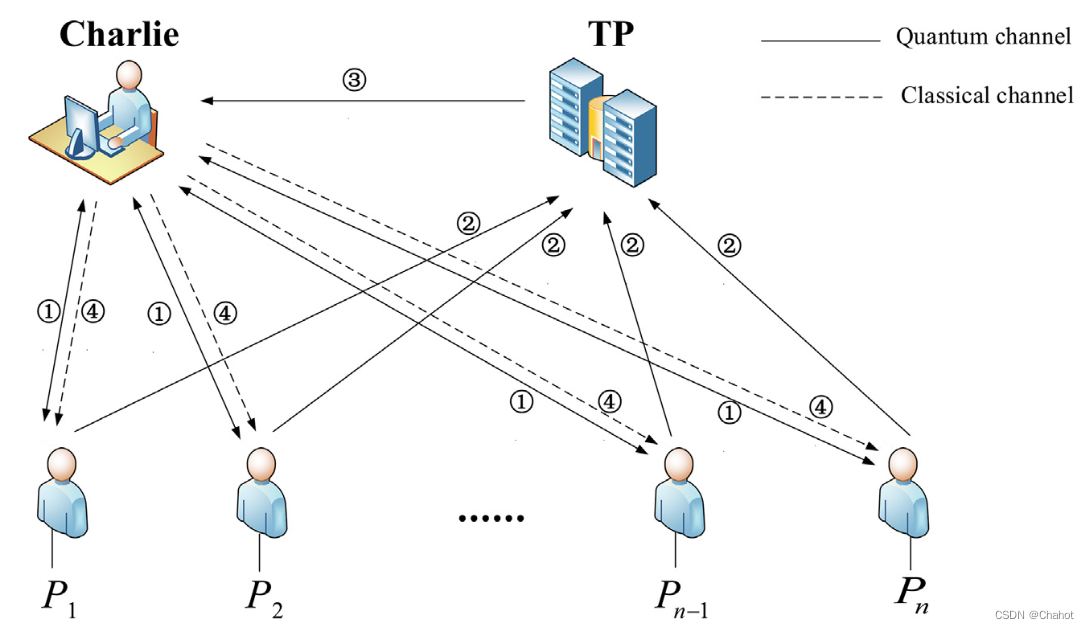
同样，TP对加密后的数据进行同态求值后，即在σ_M上应用一个Clifford门，用G_M表示。根据密钥更新规则，解密的泡利算子为$X^{\gamma }{Z}^{\delta }(\gamma ，\delta \in {[0,1]}^n)$，密文记录为$\sigma M^{\prime }$。对于任意$\rho M\prime =G_M{\rho }_M{G}_M^{†}$，求值数据为

由上式可得，即使TP和窃听者捕获了完整的加密状态和求值状态，没有解密也是无意义的。换句话说，我们的MQPC协议具有防止外部攻击的能力，同时确保原始私有信息的完美安全性。

内部攻击

参与者攻击被认为是一种通用的攻击方法，它会给一些加密协议带来一些严重的安全漏洞。在我们的协议中，参与者和TP之间不存在勾结，因此需要考虑以下两种情况。第一种情况是假设一个不诚实的参与者P_e(1≤e≤n)想要从一个诚实的参与者P_h(1≤h≤n)那里窃取隐私数据，其中e = h。但Ph通过MDI-QKD协议获得了一个安全的加密密钥，并在没有其他参与方参与或协助的情况下对隐私数据进行了加密。不诚实的参与者Pe在第2步或第3步将加密数据或评估数据从Ph传输到TP的过程中，试图发起拦截和重传攻击，将被视为外部攻击者。在前一节中，已经证明了我们的协议是安全的，可以抵御外部攻击。第二种情况是，存在n−1个不诚实的参与者共同窃取左边参与者的隐私数据，因为在这种极端情况下，不诚实的参与者拥有最大的权力。在不失一般性的前提下，假设不诚实的参与者P1, P2，…， Ph−1,Ph+1，…， Pn串通获取诚实参与者Ph(1≤h≤n)的隐私数据。即使他们串通获取$X_h^a{Z}_h^b|{\Phi }_h⟩$和ρ_M ‘，如果没有正确的解密，他们也无权访问Ph ‘的隐私数据。同时，该协议所基于的QHE方案具有信息理论上的安全性，保证了隐私数据的完美安全性。因此，它可以抵抗参与者的攻击和合谋攻击，大大提高了MQPC协议的安全性。

第三方攻击

TP攻击是威胁协议安全性的另一种内部攻击。通过5.1节的分析可以发现，在我们的工作中，在QOTP之后，TP只能得到量子完全混合态$I_{2n}/2^n$。根据QHE方案的性质，可以在不需要解密的情况下进行期望的计算。在TP对加密后的数据进行评估计算后，得到的结果仍然是密文，因此TP无法获知每个参与者所拥有的具体私有信息。因此，TP在我们的协议中几乎是不诚实的。一方面，TP负责根据需要执行同态计算，而不会与任何参与者发起串通攻击。另一方面，它可以采取一切可能的攻击手段来窃取参与者的隐私数据，但在协议的整个过程中无法获得ρ _M。同时，加密密钥是参与者和可信密钥中心通过MDI-QKD协议获取的安全密钥。如果TP公布的测量结果是假的，在错误检测过程中，适当确定序列的长度，就会有一定的概率发现它。而TP无法通过测量结果判断参与者和Charlie制备的量子态是X基还是Z基。QOTP方法使每对密钥只在加密阶段使用一次。即使随着时间的推移，密钥的规则也无法追踪，因此TP无法推断密钥的内容。因此，我们的协议可以抵抗TP的攻击。

安全分析的密钥中心

可信密钥中心Charlie的职责是与MDI-QKD协议中的每个参与者完成安全密钥分发，并更新密钥以解密比较结果。正确的比较结果将在我们的MQPC协议中由Charlie可信地宣布，这样可以防止不诚实的服务器宣布虚假的比较结果。综上所述，通过以上分析，基于QHE的MQPC协议在安全性方面具有良好的性能。

版权声明：本文的技术内容与方案来自于论文[Improved multiparty quantum private comparison based on quantum homomorphic encryption]。 本文仅在新方法的广泛传播与学习领域使用。

今天的文章基于量子同态加密的改进多方量子私有比较分享到此就结束了，感谢您的阅读。