mfc画直线的函数_函数对称变换「建议收藏」

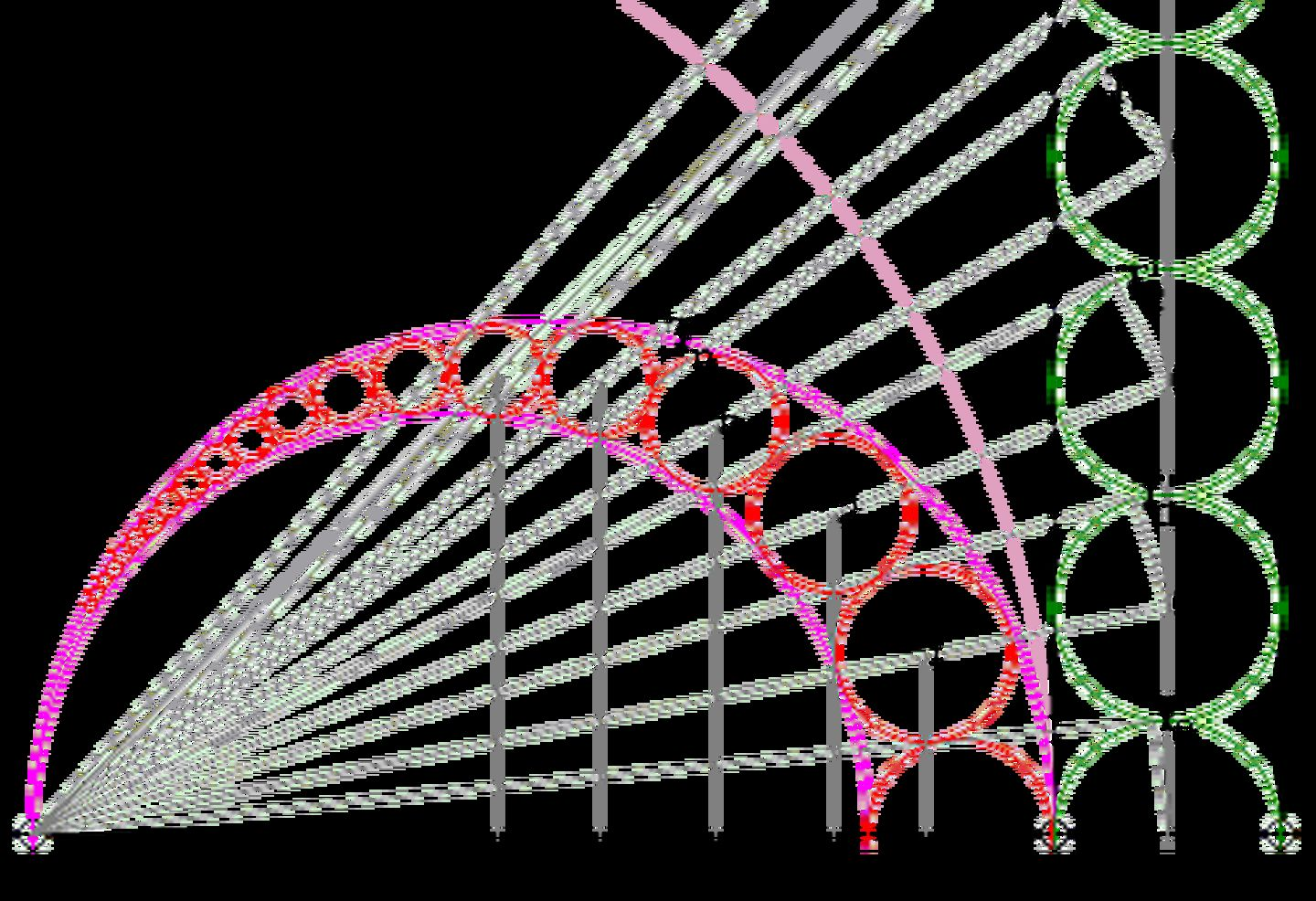
如果我说阿波罗尼奥斯问题恐怕会让人感到陌生，但是，如果我说：

画一个圆，与已知的三个圆相切。

那这个问题就让人感到十分亲切了。

这是一个平面几何上的著名问题。利用一般的方法难以求解，但是我接下来要介绍的这个基本变换可以很容易的解决这个问题。

基本变换——反演

反演变换是一种基本的几何变换。设在平面内给定一点

和常数

（

不等于零），对于平面内任意一点

，确定

′，使

′在直线

上一点，并且有向线段

与

′满足

·

′

，我们称这种变换是以

为的反演中心，以

为反演幂的反演变换，简称反演。称

′为

关于

的互为反演点。

一般我们所讨论的反演变换都是关于圆周或球面的反演。

我理解的反演变化是关于圆周（球面）的对称变换。我们所熟悉的关于一条直线的对称变化的性质是：原像与像全等。即两者大小和形状在对称变换前后保持一致：

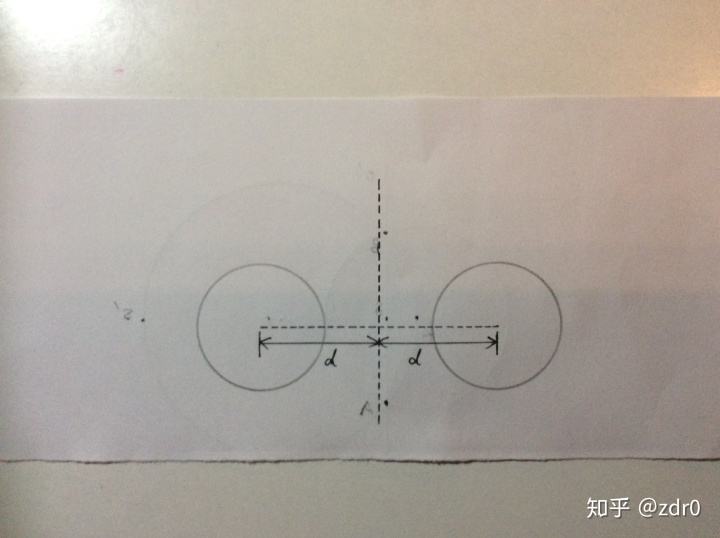
那么关于圆的反演变换（今后若不加特殊说明，直接简称为反演变换）是如何定义的呢？变换前后的图像之间又有何关系呢？

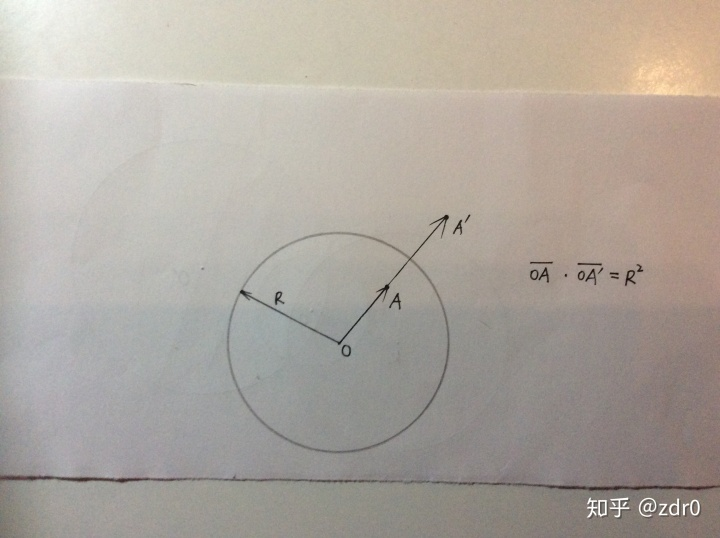
我们设有一个半径为

的圆，圆心为

。则圆内一点

与其变换点

´满足关系式：

显然，圆周上的点的反演使其本身。

我们讨论几种不同的情况下的反演变换，看看变换前后的图形之间有何区别。

• 过
  

  的直线

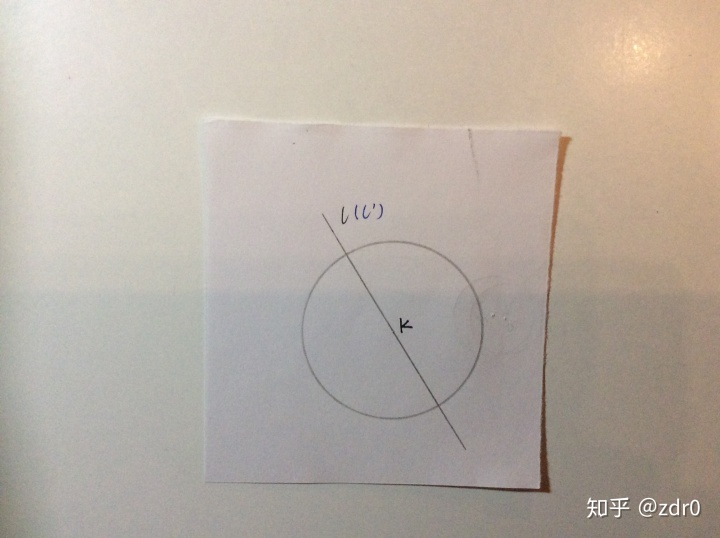
首先结论是：过

的直线

的反演是其本身。

这个比较好理解，我们观察直线上的点：直线上在圆内部的所有点都被反演到圆外部，直线与圆的交点的反演还是交点，直线上在圆外部的点都被反演回圆内部，圆心

与无穷远点互为像与原像。且由于直线过圆心，则所有反演之后的点都沿直线的方向向量排列。所以，过圆心的直线的反演是其本身。

• 不过
  

  的直线和过

  

  的圆

结论是：这两者互为逆变换。

由于两者互为逆变换，那我就只在一个方向说明好了。

首先，不过圆心的直线又可分为以下三种情况

1. 该直线与圆有两个交点（相交）

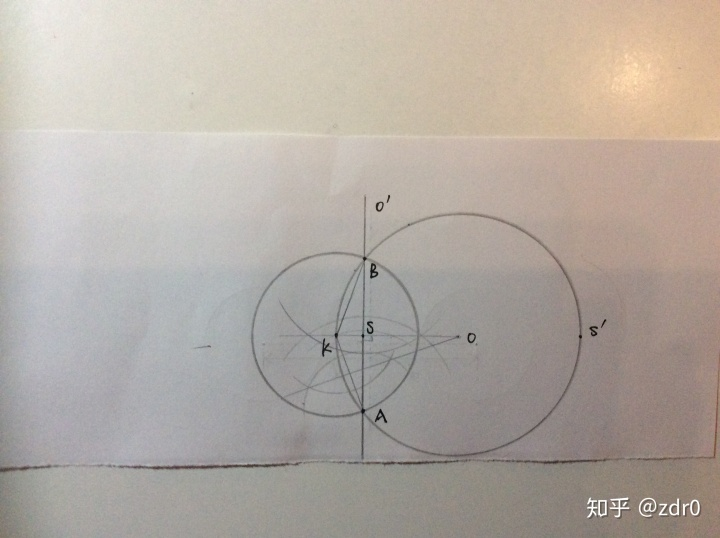
这种情况下该直线与圆的两个交点的反演还是其自身，且该直线上在原始圆内部的点被反演到原始圆的外面，且由于该直线不过原始圆的圆心，所以，这些点被反演出去会变成一段规则的弧（优弧

），设该弧的中点为

。直线上在原始圆外部的点会被反演回原始圆的内部，且无穷远点的反演点是原始圆的圆心。现在，我们画出直线在圆内部分的垂直平分线，该线段与其垂直平分线的交点记为

。显然，