几何中的点_立体几何三线共点例题

点与线

直线的表达方式

直线表达形式有很多，我们重点讲一般式和斜截式

• 一般式: ax + by + c = 0
• 斜截式: y = kx +b

两点确定一条直线，所以我们将直线用两个点表示

struct Line
{ 
   
    Point p1, p2;
    Line() { 
   }
    Line(Point p1, Point p2) :p1(p1), p2(p2) { 
   }
    Line(Point p, double angle) //0<=angle<pi
    { 
   
        p1 = p;
        if (sgn(angle - pi / 2) == 0)
        { 
   
            p2 = p1 + Point(0, 1);
        }
        else
        { 
   
            p2 = (p1 + Point(1, tan(angle)));
        }
    }
    //ax+by+c=0
    Line(double a, double b, double c)     
    { 
   
        if (sgn(a) == 0)
        { 
   
            p1 = Point(0, -c / b);
            p2 = Point(1, -c / b);
        }
        else if (sgn(b) == 0)
        { 
   
            p1 = Point(-c / a, 0);
            p2 = Point(-c / a, 1);
        }
        else
        { 
   
            p1 = Point(0, -c / b);
            p2 = Point(1, (-c - a) / b);
        }
    }
};

线段的表示

typedef Line Segment;		//与直线扩展到向量类似

点与直线的位置关系

我们把点与直线的关系分为点在直线的左侧，右侧和在直线上

int Point_line_relation(Point p,Line v)
{ 
   
	int c=sgn(Cross(p-v.p1,v.p2-v.p1));  //计算叉积的正负从而加以判断
	if (c<0) return -1;		//p在v左侧
	if (c>0) return 1;		//p在v右侧
	return 0;				//p在v上
}

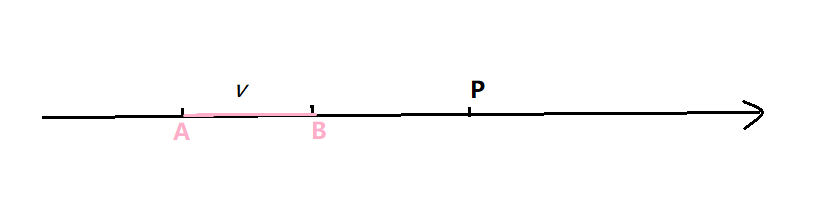
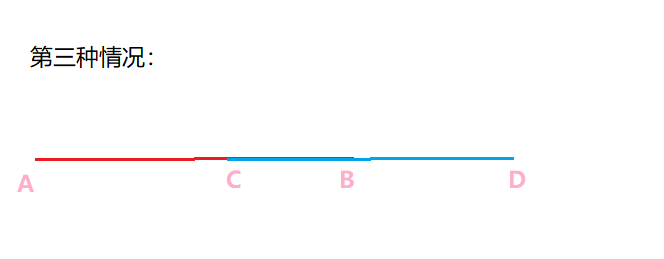
点与线段的位置关系

判断点P在直线v上，首先，用叉积判断是否共线，但这还不过，可能出现一下特殊情况

此时，就需要再加一条判断条件：P与v的两个端点夹角是否为钝角(180°)

bool Point_on_seg(Point p,Line v){ 
   
	return sgn(Cross(p-v.p1,v.p2-v.p1))==0&&sgn(Dot (p-v.p1,v.p2-v.p1))<=0;
}

点到直线的距离

可把点和线补成平行四边形，这所求距离即为平行四边形的高

double Dis_point_line(Point p,Line v){ 
   
	return Cross(p-v.p1,v.p2-v.p1)/distance(v.p1,v.p2);
}

点在直线上的投影

以下是证明过程：

double Point_line_proj(Point p,Line v){ 
   
	double k = Dot(v.p2-v.p1,p-v.p1)/Len2(v.p2-v.p1);
	//Len2为求p1p2长度的平方的函数（自定义），前面并未给出
	return v.p1+(v.p2-v.p1)*k;
}

点关于直线的对称点

我们先借助上面的函数球场投影，再求出对称点

Point Point_line_symmetry(){ 
   
	Point q = Point_line_proj(p.v);
	return Point(2*q.x-p.x,2*q.y-p.y);		//两点中点坐标公式变形
}

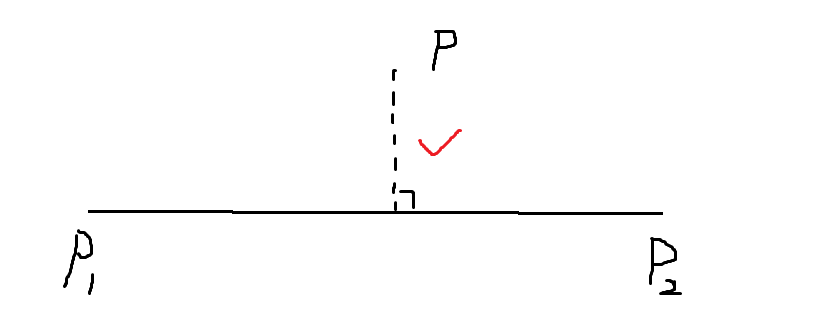
点到线段的距离

如果p1,p2在P两侧，则最短距离为点到线段的垂直距离

但如果p1,p2在P同侧，则不存在垂直距离

所以需先判断p1,p2是否在P同侧，再根据不同情况利用距离公式计算

Point Dis_point_seg(Point p,Segment v){ 
   
	if (sgn(Dot(v.p2-v.p1,p-v.p1))<0||sgn(Dot(p-v.p2,v.p1-v.p2))<0)
		return min(Distance(p.v1,p),Distance(p.v2,p));
	return Dis_point_line(p,v);
}

两直线位置关系

直线的位置关系分为重合，平行和相交

int Line_relation(Line v1,Line v2){ 
   
	if (sgn(Cross(v1.p2-v1.p1,v2.p2-v2.p1))==0){ 
   
		if (Point_line_relation(v1.p1,v2)==0) return 2;		//重合
		else return 0;										//平行
	}
	return 1;												//相交
}

求两直线（线段）交点

证明过程如下：
直接上代码

Point Cross_point(Point a,Point b,Point c,POint d){ 
   		
	//Line1:ab,Line2:cd
	double s1=Cross(b-a,c-a);
	double s2=Cross(b-a,d-a);
	return Point(c.x*s2-d.x*s1,c.y*s2-d.y*s1)/(s2-s1);
}

注： 在只用此公式时应确保Line1和Line2相交，否则s2-s1=0造成除零运算

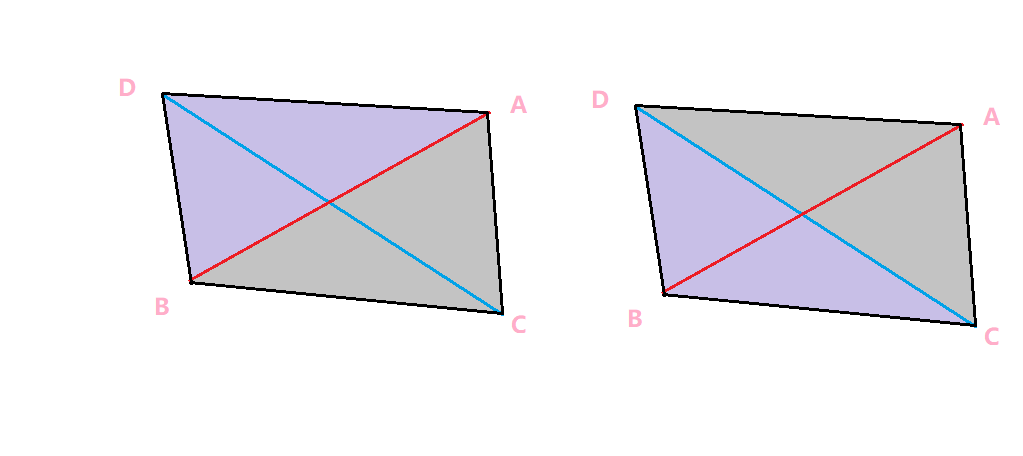
判断两直线是否相交

利用叉积的正负，如果相交，图中不同颜色模块的面积应该为相反数

bool Cross_segment(Point a, Point b, Point c, Point d) { 
   
	//Line1:ab,Line2:cd
    double c1 = Cross(c - a, b - a), c2 = Cross(d - a, b - a);
    double c3 = Cross(d - c, a - c), c4 = Cross(d - c, b - c);
    return sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0;
}

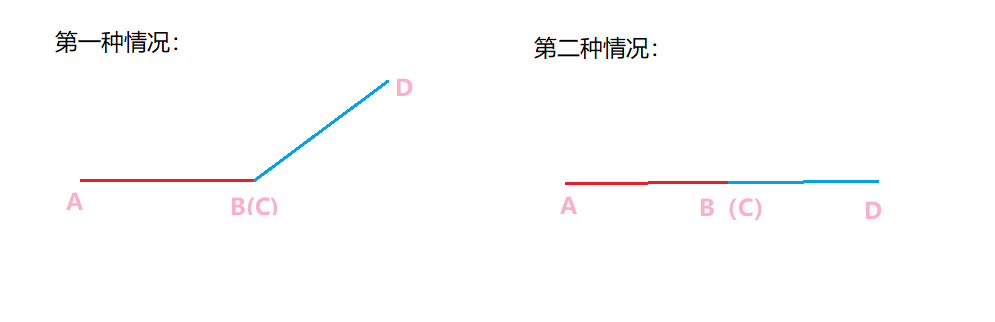
以上代码还存在缺陷，如果出现下列情况将会判断错误


所以此时需要特判

持续更新。。。。。。

今天的文章几何中的点_立体几何三线共点例题分享到此就结束了，感谢您的阅读。