心电信号处理算法设计-实验要求
- data4 是一段实际采样得到的心电数据, 采样频率为 100Hz, 波形如下图所示。设计相应的算法, 计算心率, 单位为: 次/分钟。可能会用到的知识为数字滤波器的设计, 离散傅里叶变换等。要求该算法复杂度尽量简单, 可以移植到 Cortex-M3性能的单片机上实现(本次不需要做移植, 只需要考虑算法的复杂度即可)。可选择自己熟悉的语言进行算法设计, 建议选择 Matlab 进行算法设计。
- 同样是 data4 实际采样得到的心电数据, 对该数据进行相应的处理, 得到标准的心电波形。要求能够显示完整的 PQRST 的心脏跳动过程, 能够清楚的看到处理后的心电信号显示 P 波、R 波和 T 波。幅值(y 轴)可以不做处理, 或者为了计算方便也可以做归一化处理, 不做具体要求。
- 认真撰写设计报告, 要求有详细的算法设计说明, 可以选择文字、流程图等图文配合对算法进行说明。若参考了学术论文, 请注明参考文献。
准备工作:
| 数据 | 备注 |
|---|---|
| 采样频率 | 100Hz |
| 数据数量 | 1868条 |
| Matlab版本 | 2015b |
| 操作系统 | XUbuntu20.04 |
| 流程图绘制工具 | LibreOffice Draw |
原始信号组成:
| 信号 | 频带范围 | 滤波器 |
|---|---|---|
| 心电信号 | 5~20HZ[1] | – |
| 肌电噪声 | 30~300Hz[1] | 低通 |
| 工频噪声 | 50Hz[1] | 低通 |
| 基线漂移噪声 | 0.03Hz[2] | 零相移滤波器 |
实验总流程图:
#########第1部分.设计相应的算法, 计算心率####################
概述:
①肌电噪声和工频噪声处理
主要代码来自[1],[1]中滤除肌电噪声和工频噪声各自用了一个滤波器,
属于多余,保留最低截止频率的低通滤波器即可.
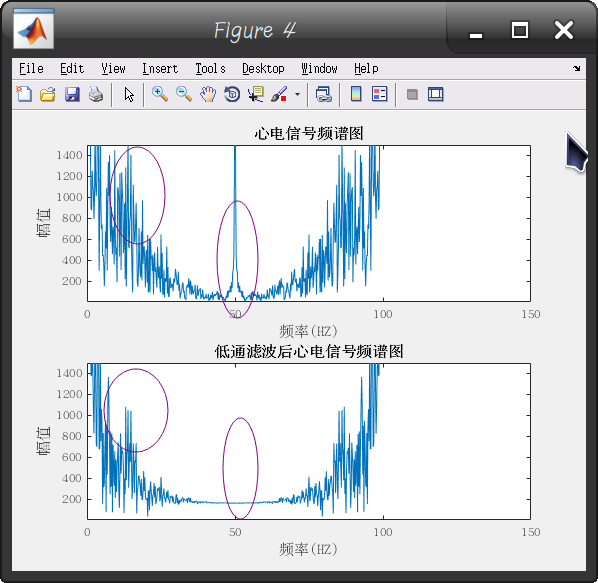
过滤后效果如下:
fp=10;%通带截止
fs=15;%阻带截止频率
可以看到:
①50Hz工频被滤除
②20Hz以上信号被削弱
③之所以两边呈现对称都有是因为傅里叶变换有双边效果.
———————————————————————-
②基线漂移噪声处理
[1]中的零相移(分子分母各自的相位偏移理论计算上一致称为零相移)
滤波器代码不完整,且没给截止角频率和阶数
[2]中式(4)为:
H ( z ) = 09876 z − 0.9876 z − 0.9752 H(z)=\frac{09876 \mathrm{z}-0.9876}{z-0.9752} H(z)=z−0.975209876z−0.9876
可知零相移滤波器的阶数为1
∵基线漂移噪声的频率远远低于心电信号,
∴基线漂移滤波器的截止频率设为比”心电信号的频率下限”小一些即可.
———————————————————————-
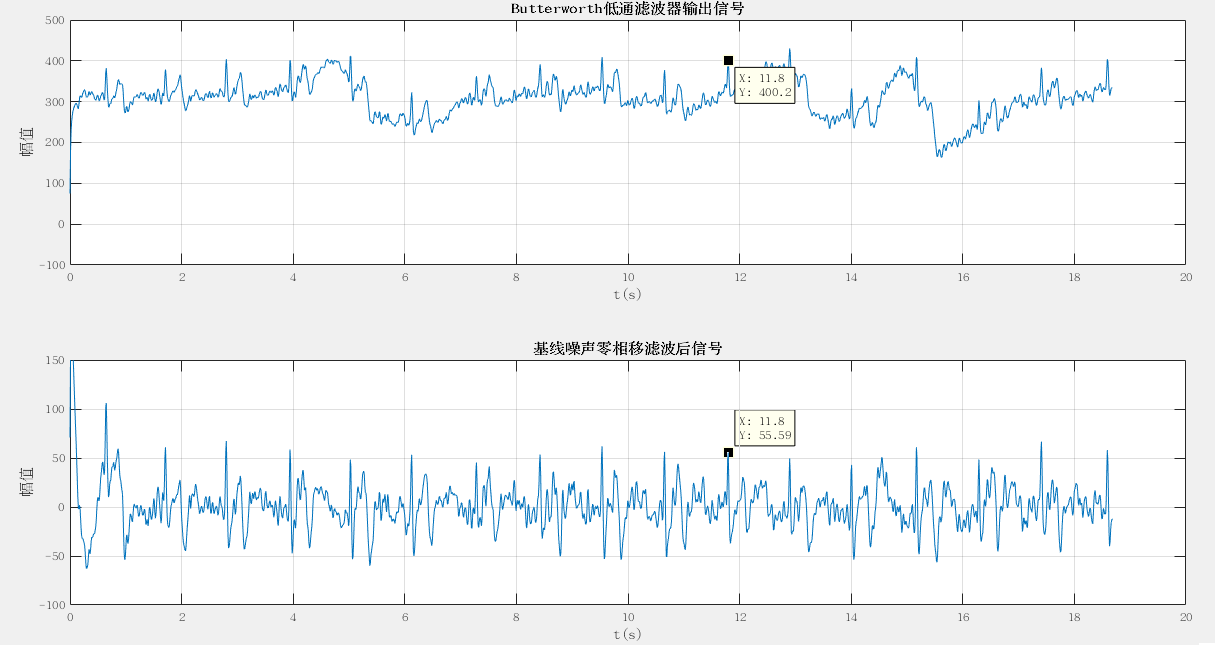
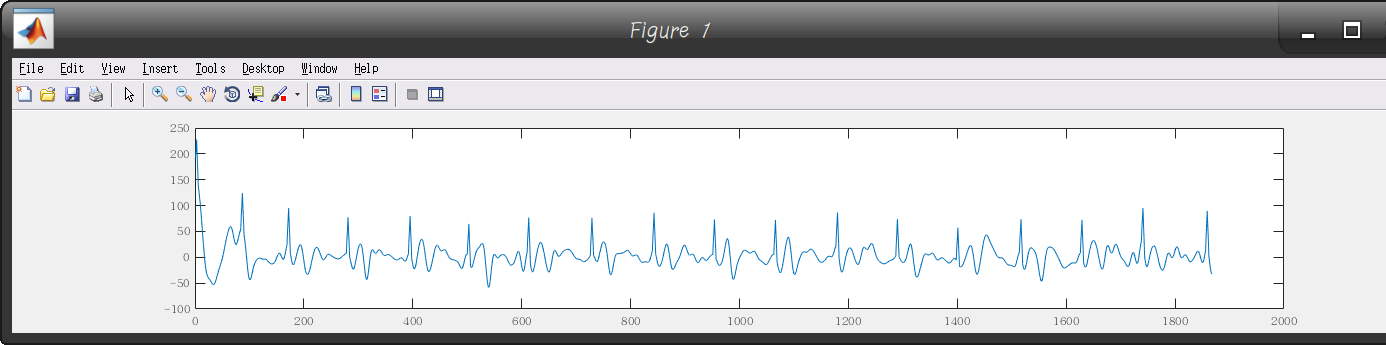
③经过上面的两步处理,最终得到如下波形:
在上面两图中对比波峰,可以看到波峰所在时刻点位置对应,所以确实是零相移。
———————————————————————-
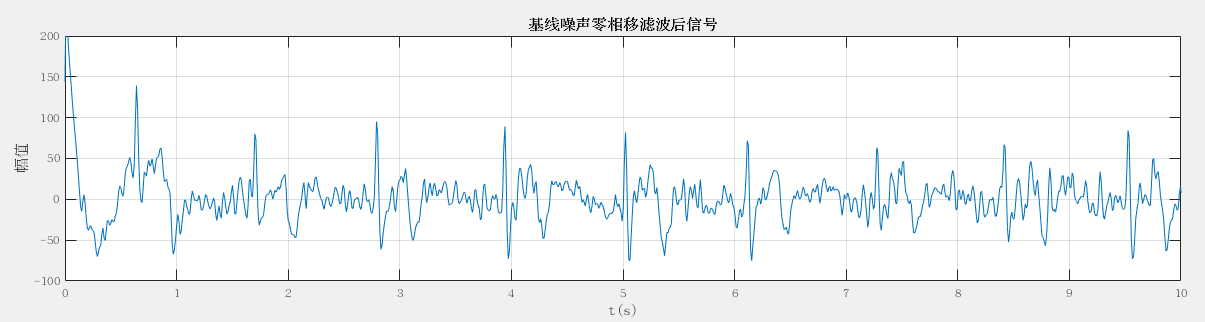
④对比[3]中的心患波形与③中波形(为了便于比较,经过放大处理):
| 实验结果 | [3]房扑图 |
|---|---|
 |
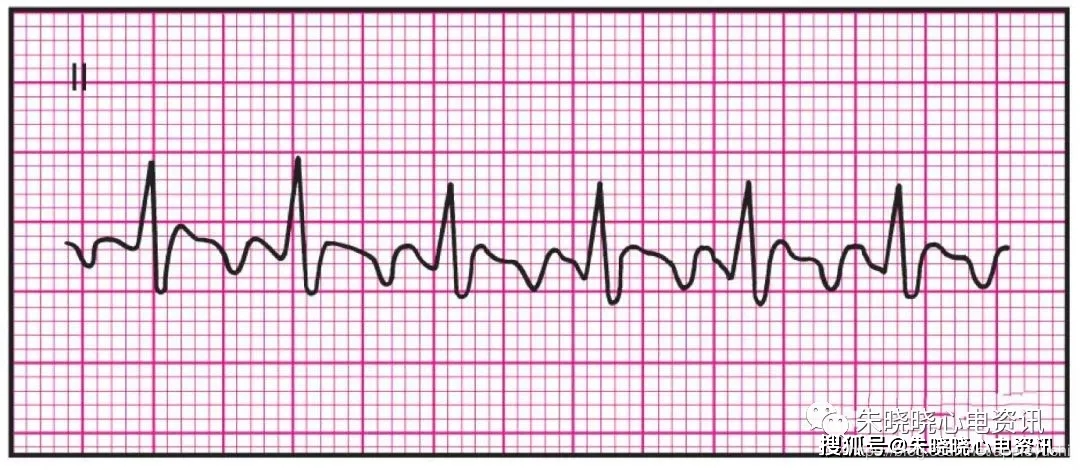 |
依据上述比较可以判断:
该心电信号来源于患有”房扑”的心脏病人.
———————————————————————-
⑤波峰检测:
| 采样时刻(s) | 波峰 |
|---|---|
| 0.0100 | 229.6991 |
| 0.8600 | 62.4065 |
| 1.7100 | 72.1880 |
| 2.7900 | 82.7408 |
| 3.9400 | 81.1390 |
| 5.0200 | 72.2794 |
| 6.1200 | 65.1390 |
| 7.2800 | 55.6109 |
| 8.4200 | 62.6077 |
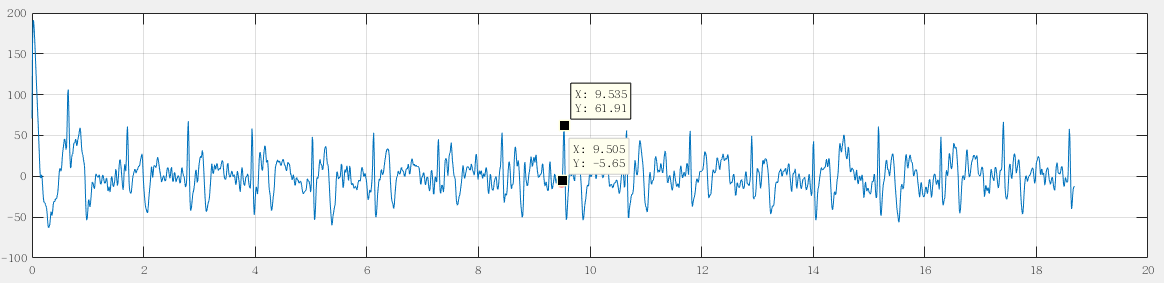
| 9.5300 | 75.2257 |
| 10.6400 | 71.2959 |
| 11.7800 | 69.1398 |
| 12.8900 | 66.7628 |
| 13.9900 | 58.2763 |
| 15.1600 | 86.7839 |
| 16.2800 | 64.3633 |
| 17.4000 | 77.9292 |
| 18.5800 | 76.4417 |
对照③中的图,确实是18个波峰,说明代码输出正确。
数据清洗:
①第一条数据是异常数据,删除.
②第二条数据和第三条数据时间间隔小于1s,所以也要删除。
计算心率的处理步骤:
①计算第一列的其余数据的相对于上一条数据的时间间隔(详细细节请见[6]),得到一个序列
②将①中的序列计算加权平均,得到心跳一次的耗时
③60s/心跳一次的耗时,可以得到平均心率(每分钟心跳多少次)。
实验第1部分结论:
该心电信号的心率为53.35次/分
算法复杂度分析:
这个要看底层被调用的代码有哪些地方用for循环了,
没有来得及去看。
第1部分代码不靠谱的地方:
使用了零相移滤波器,
实际中不可能零相移(不知道硬件中效果如何),
以及阶数512(硬件开销较大),
可能需要后面再改。
#############-第2部分-PQRST模拟#############
根据[4],目前没有能直接处理实验第1部分中③中结果的波形.查看了文献[5],都是很理想很光滑的输入波形,不适合本例。
[4][5]的共同特点都是对光滑密集的输入波形进行PQRST模拟。③中波形布满噪声,故下面试图处理该问题。
开始观察波形并进行分析:
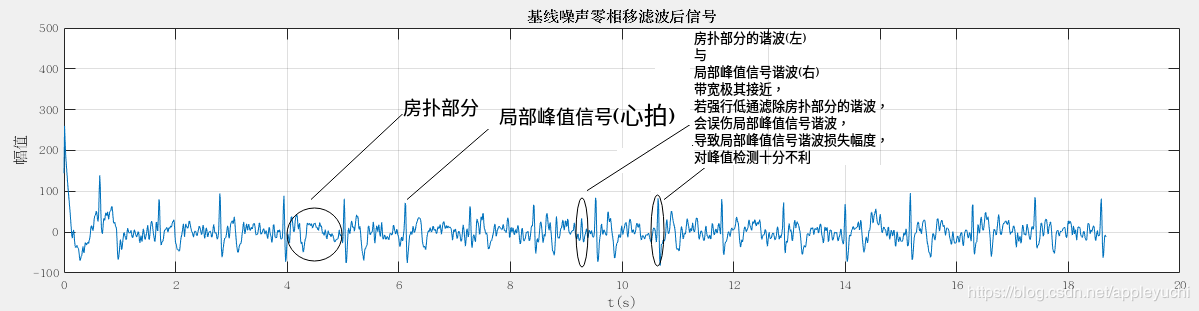
∵实验报告第1部分的③最终判定该心电信号属于”房扑”
∴所以上述除了最高尖峰以外的部分波形中,
判定波谷属于有效信号,予以保留,
高频波峰视为需要去除或平滑的噪声.
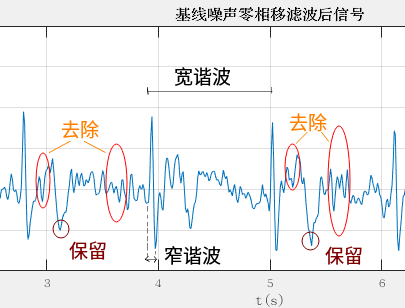
这里有个矛盾:
峰值(心拍)所处的位置,至少有两种谐波,
一种是窄谐波,一种是宽谐波。
窄谐波(高频):构成峰值的形状.
宽谐波(低频):构成心率周期波形
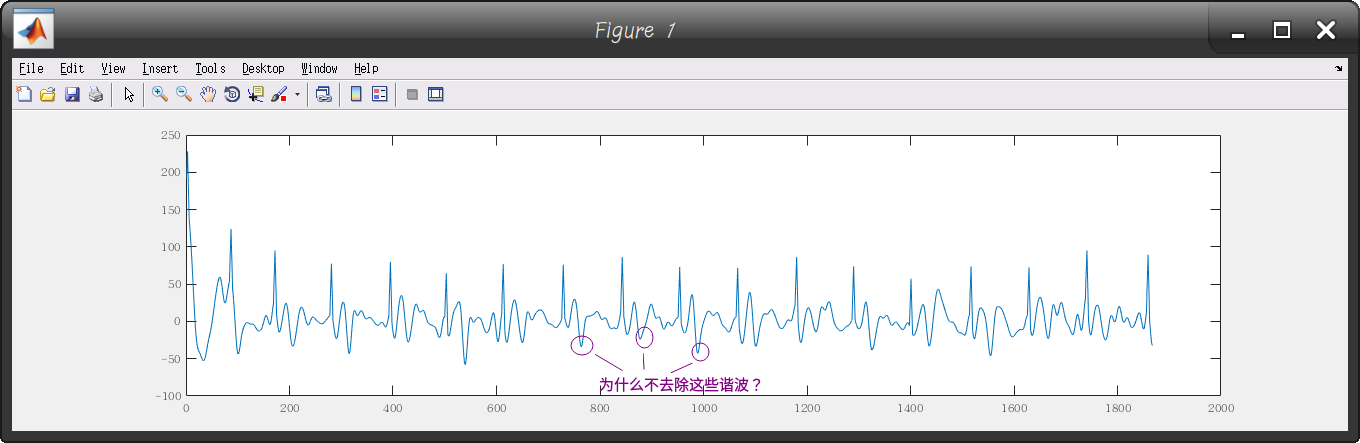
信号分析:
①
∵因为窄谐波和噪声谐波宽度很接近,也就意味着两者频率接近。
∴如果滤除图中标记的噪声,那么窄谐波也会被”误伤”滤除,“误伤”会导致心率难以计算.
所以只能是先计算心率,再进行PQRST模拟,不可能反着来
②如果不滤除图中标记的噪声,那么会导致无法使用[4]中的方式进行PQRST模拟,想要进行PQRST模拟必须滤掉房扑部分的噪声,同时不能误伤峰值(心拍).
下面考虑几种方案来设法平滑该信号:
| 可能的方案 | 存在的问题 |
|---|---|
| 指数平滑+峰值(心拍)恢复 | ①会滞后一个采样时刻,需要恢复 ②需要恢复峰值(心拍) |
| 小波变换+峰值(心拍)恢复 | 需要恢复峰值(心拍) 好处是滤噪后没有相移 |
最省事的目前想到的应该是小波变换了。
要如何恢复被小波变换误伤的峰值信号(心拍)呢?
我们观察到波峰到波谷大概是3~4个采样间隔,如下:
①实验第1部分峰值(心拍)检测时,留下了峰值(心拍)对应的时刻位置
②小波变换过滤噪声
③通过①中的峰值(心拍)位置,在该位置±3个采样间隔(本实验中±0.03s),对信号进行增强处理。增强处理办法如下:
峰值中心增强70mv,
峰值中心±0.01s处增强45mV
峰值中心±0.02s处增强25mV
峰值中心±0.03s处增强10mV
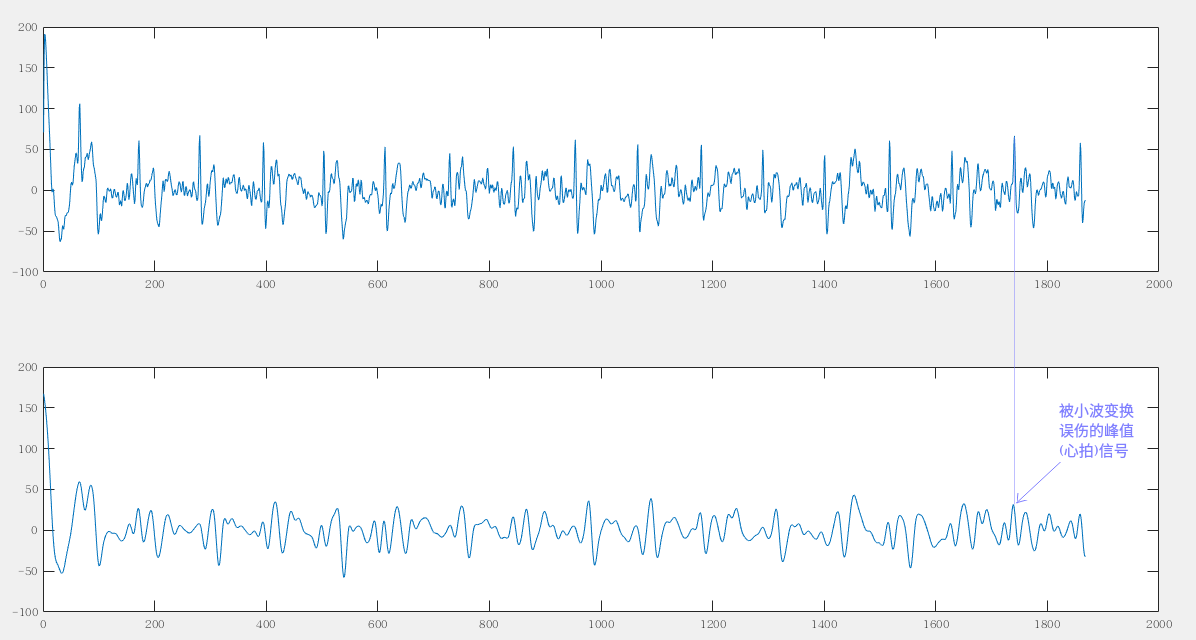
小波变换处理后效果如下:
峰值信号(心拍)增强后效果:
为什么不消除上图中标记的噪声谐波?是不是实验处理有问题?
因为您提供的是“房扑“心电信号,而不是“健康“心电信号。
如果去除了,会把心脏病误诊为心脏健康。
所以不应该去除。
实验第2部分结论-总体效果
实验第2部分结论-局部放大效果
除了上面论述的通过小波变换进行PQRST模拟,
还可以通过指数平滑进行PQRST模拟,相关实验报告请见参考文献[7]
可以得到与上面类似的效果.
附录
原始数据、完整代码、运行步骤:
https://gitee.com/fastsource/heart_rate_pqrst
Reference:
[1]基于MATLAB的心电信号预处理
[2]Filters in the ECG Signal Processing
[3]常见的14种异常心电图的波形特点
[4]心电信号的PQRST模拟matlab代码(转载+自己调研汇总)
[5]傅里叶级数在心电信号模拟中的应用
[6]根据心电信号计算心率的matlab代码
[7]基于指数平滑对心电信号进行PQRST模拟
今天的文章数字信号处理实验报告_数字信号处理实验报告分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/88120.html