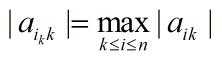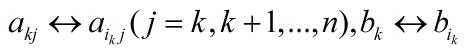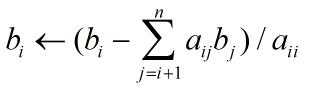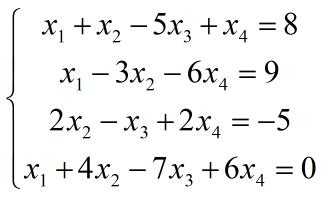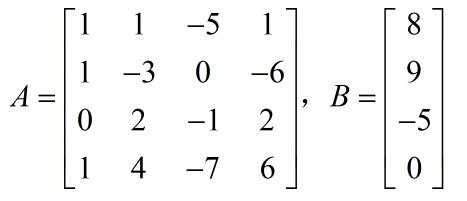列主元消去法matlab代码_列主元消去法例题详解

一、Gauss消去法与列主元素消去法的联系与区别

    Gauss消去法有以下两个主要缺陷：

    1）如果某个主元akk=0，则消元无法进行；

    2）在akk=0，但相对很小，当其作为除数时，会导致其他元素数量级的增长，容易造成严重的舍入误差。

    而主元素消去法则是对Gauss消去法存在的两个主要问题的一种解决方法。

    联系：主元素消去法本质上还是Gauss消去法，前者克服了后者存在的主要缺陷；两种方法都只适合于低维的计算。

    区别：主元素消去法的鲁棒性更强，但计算量比Gauss相对来说要多出排序这一部分。

    主元素消去法使用地比较多的是列主元素消去法，与Gauss消去法的主要区别是在进行第k次更新时，首先需要对第k列的第k行以及该列后续元素进行排序，并交换得到最大元素的行。由于消元过程与Gauss过程基本相同，回代过程完全一样，因此不再赘述，详细过程请参考《 Gauss消元法的Matlab实现 》

二、算法描述

    1）消去过程

    对k = 1,2,…,n-1，有：

   （1）按列选主元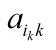，即：

   （2）若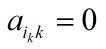，则停止计算（此时det(A)=0）

   （3）若ik = k，则转向（4），否则换行，即：

   （4）消元计算

        对i = k+1, k+2, …, n,

        lik = aik/akk, (|lik |≤1),

        对j = k+1, k+2, …, n,

        aij←aij – likakj,

        bi←likbk

   2）回代过程

     1）若ann = 0，则停止计算，det(A) = 0，否则

        bn←bn/ann

     2）对i = n-1, n-2, …, 1,

三、列主元素消去法的Matlab实现

    实现代码如下：

    主函数：

function [r_matrix,time_] = MainElementElimination(Coefficient_matrix,Load_matrix)
%  主元素消去法的matlab实现
%  2017-11-05 by xh_scu
%  inputs:
%         A_matrix:系数矩阵，维度为n*n
%         B_matrix:载荷矩阵，维度为n*1
%  outputs:
%         result:未知量矩阵，维度n*1
% 计时开始
t1 = clock;
% 判断输入矩阵维度是否满足要求
[row_coeff,col_coeff] = size(Coefficient_matrix);
[row_load,~] = size(Load_matrix');
% 初始化r_matrix矩阵
r_matrix = zeros(row_load,1);
% 判断输入的维度是否满足要求
if (row_coeff ~= col_coeff) || (row_coeff ~= row_load) % if-1
    % 不满足则输出错误提示
    print('输入错误！');
else
    % 满足则进行下一步运算
    for k = 1:row_coeff-1 % for-1
        % 检查主对角元素第i行的第i个元素是否为0
        if Coefficient_matrix(k,k) == 0 % if-2
            print('主对角元素错误！');
            break;
        else
            % 找到第k列从第k行开始的最大元素
            % 获取第k列
            col_k = Coefficient_matrix(:,k);
            max_index = find_max(col_k,row_coeff,k); % 注：此处需要调用函数max_find()
            %如果最大值索引不是k，则交换第k行与max_index行
            if max_index ~= k % if-3
                for i_change = k:col_coeff % for-2
                    temp = Coefficient_matrix(max_index,i_change);
                    Coefficient_matrix(max_index,i_change) = Coefficient_matrix(k,i_change);
                    Coefficient_matrix(k,i_change) = temp;
                end % for-2
                % 交换负荷矩阵
                temp_k = Load_matrix(k);
                Load_matrix(k) = Load_matrix(max_index);
                Load_matrix(max_index) = temp_k;
            end % if-3
            % 循环计算第k+1行到最后一行
            for i = k+1:row_coeff % for-3
               L_ik = Coefficient_matrix(i,k) / Coefficient_matrix(k,k); %更新L_ik
               % 更新每一行从第i个元素开始后的所有元素
               for j = k+1:col_coeff % for-4
                   Coefficient_matrix(i,j) = Coefficient_matrix(i,j) - ...
                       L_ik*Coefficient_matrix(k,j); % 更新a(i,j)
               end % for-4
               Load_matrix(i) = Load_matrix(i) - Load_matrix(k)*L_ik; % 更新b(i)
               Coefficient_matrix(i,1) = 0; 
            end % for-3
        end % if-2
    end % for-1
    % 回代过程
    r_matrix(row_coeff) = Load_matrix(row_coeff)/Coefficient_matrix(row_coeff,col_coeff);
    for k = row_coeff-1:-1:1 % for-5
        sum_temp = 0;
        for j = k+1:col_coeff % for-6
            sum_temp = sum_temp + Coefficient_matrix(k,j)*r_matrix(j);
        end % for-6
        r_matrix(k) = (Load_matrix(k) - sum_temp)/Coefficient_matrix(k,k);
    end % for-6
end % if-1
% 计时结束
t2 = clock;
time_ = etime(t2,t1);
end % 函数结束

     子函数：

%%  寻找第k列从第k行开始的最大元素
function  [max_index] = find_max(input_k,row_,k)
%  inputs:
%         input_k:第k列的所有元素
%         row_   :矩阵的总行数
%         k      :第k列序号
%  outputs:
%         max_index:第k列从第k行以后最大元素的行下标

% 初始化参数
max_index = k;
max_val = input_k(k);
for i = k:row_   % for-1
    if max_val < input_k(i)  % if-1
        max_val = input_k(i);
        max_index = i;
    end % if-1
end % for-1
end

四、测试与分析

    设有如下方程组：

    则矩阵A与B分别为：

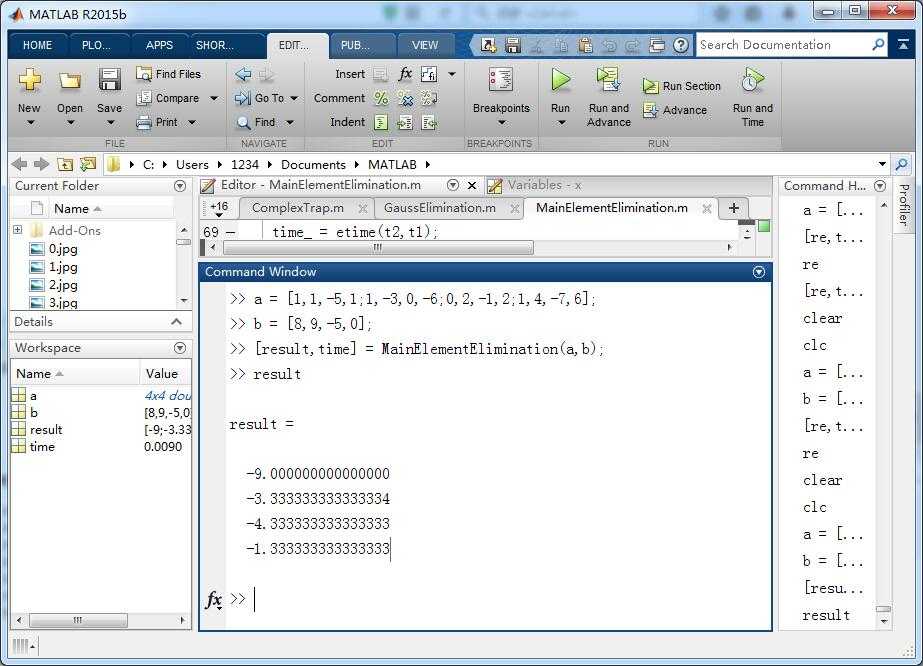
    调用代码：

a = [1,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6];
b = [8,9,-5,0];
[result,time] = MainElementElimination(a,b);

    计算结果为：

    与准确结果[-9,-10/3,-13/3,-3/4]’相等（存在计算舍入误差）。

    有兴趣的小伙伴还可以测试一下代码的计算效率，从理论上来讲，主元素消去法比Gauss消去法计算量更大，计算时间更长。这里就不再做进一步分析了。

今天的文章列主元消去法matlab代码_列主元消去法例题详解分享到此就结束了，感谢您的阅读。