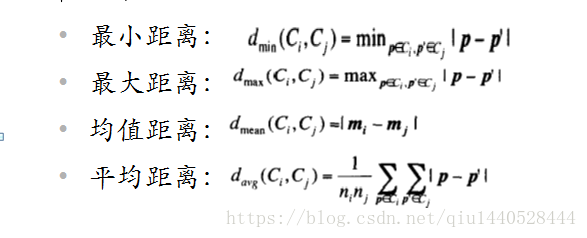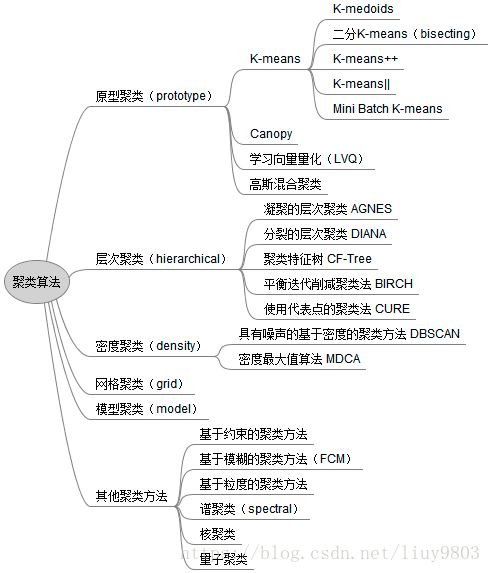
clustering 介绍

聚类的定义

聚类与分类的不同在于，聚类所要求划分的类是未知的。也就是说我们对样本数据的划分是不了解。聚类分析的任务就是要明确这个划分。例如我们采集到很多未知的植物标本，并对每株标本的植物学特征进行了记录、量化。那么这些植物标本到底是几个物种呢？聚类分析就可以解决这个问题。

聚类的评价标准

聚类质量的判断标准是簇内相似度最高、簇间差异性最高，这个标准我们如何进行衡量呢？

Calinski-Harabaz 分数

如何确定聚类的个数

Deciding the Number of Clusterings

具体方法

Mean-shift（均值迁移）

概述

均值迁移的基本思想是：
在数据集中选定一个点，然后以这个点为圆心，r为半径，画一个圆(二维下是圆)，求出这个点到所有点的向量的平均值，而圆心与向量均值的和为新的圆心，然后迭代此过程，直到满足一点的条件结束。(Fukunage在1975年提出)

后来Yizong Cheng 在此基础上加入了 核函数 和 权重系数 ，使得Mean-shift 算法开始流行起来。目前它在聚类、图像平滑、分割、跟踪等方面有着广泛的应用。

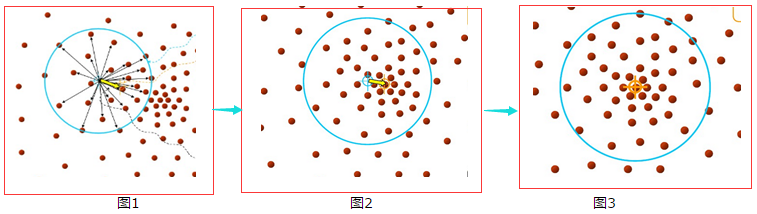
图解过程：

由上图可以很容易看到，Mean-shift 算法的核心思想就是不断的寻找新的圆心坐标，直到密度最大的区域。

Note:
需要指定类的数目。

Spectral Clustering（谱聚类）

概述

Spectral Clustering(SC,即谱聚类)，是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最优解。其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类.它与样本特征无关而只与样本个数有关。

基本思路：
将样本看作顶点,样本间的相似度看作带权的边,从而将聚类问题转为图分割问题:找到一种图分割的方法使得连接不同组的边的权重尽可能低(这意味着组间相似度要尽可能低),组内的边的权重尽可能高(这意味着组内相似度要尽可能高).

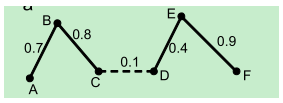
图解过程：

如上图所示，断开虚线，六个数据被聚成两类。

Note:
需要指定类的数目。

Hierarchical Clustering（层次聚类）

概述

在某些情况下，我们想把数据划分为不同层次上的群组，hierarchical clustering 就可以将数据对象组成层次结构，这种层次结构可以称为聚类树。

两种策略

按照策略可以将方法分为两种：

1. 凝聚层次聚类
   采用自底向上的策略，首先将每个对象作为一个单独的簇，然后根据某种距离度量合并这些簇形成越来越大的簇，直到所有的对象都在一个簇中（层次的最上层），或者达到一个终止条件。绝大多数层次聚类方法属于这一类。
2. 分裂层次聚类
   采用自顶向下策略，首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到每个对象自成一个簇，或者达到某个终止条件。

终止条件可以是，达到某个希望的簇的数目，或者两个最近的簇之间的距离超过了某个阀值。

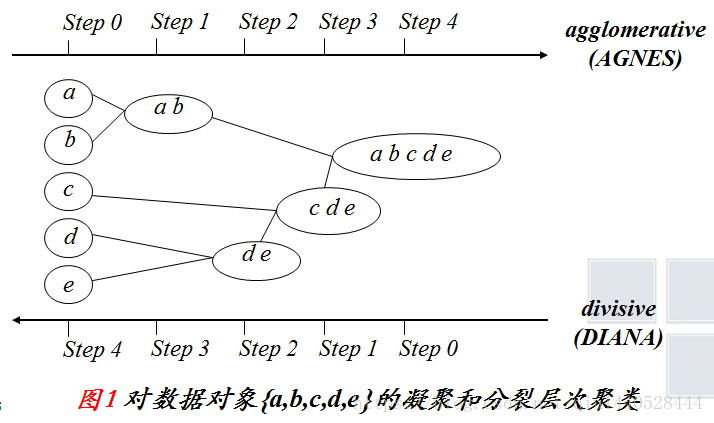
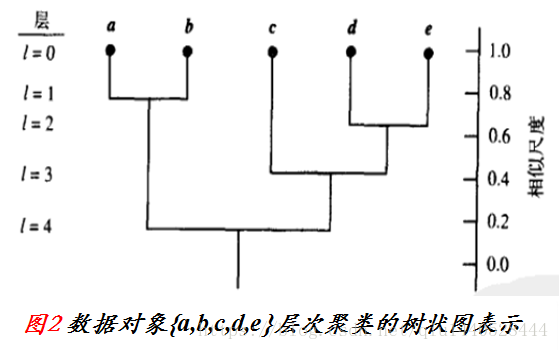
下图描述了一种凝聚层次聚类算法AGNES和一种分裂层次聚类算法DIANA对一个包含五个对象的数据集合 { a,b,c,d,e } 的处理过程。

表示方法

通常使用一种称为树状图的树形结构表示层次聚类的过程。它展示对象是如何一步步进行分组的。如下图显示上图的五个对象的树状图。

距离度量

如何度量两个簇之间的距离呢？？四个广泛采用的簇间距离度量方法如下，
( 其中$|p-p^{\prime }|$是两个对象或点$p$和$p^{\prime }$间的距离，$m_i$是簇$C_i$的质心，$n_i$是簇$C_i$中对象数目。)

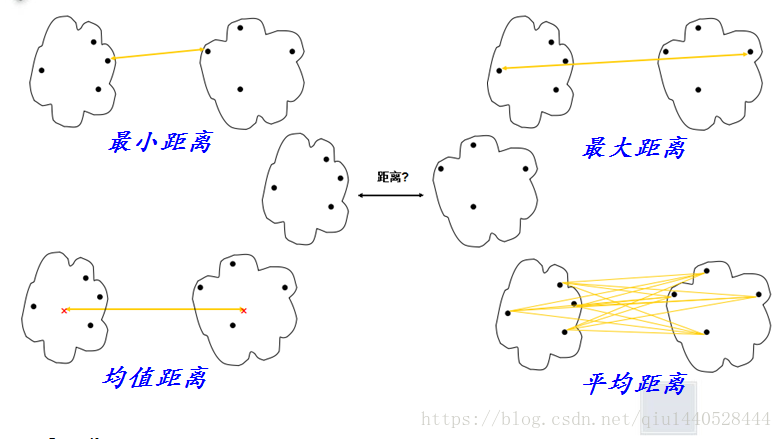
图示如下：

• 当算法使用最小距离衡量簇间距离时，有时称它为最近邻聚类算法。此外，如果当最近的簇之间的距离超过某个任意的阈值时聚类过程就会终止，则称其为单连接算法（single linkage）。
• 当一个算法使用最大距离度量簇间距离时，有时称为最远邻聚类算法。如果当最近簇之间的最大距离超过某个任意阈值时聚类过程便终止，则称其为全连接算法 (complete linkage)。

距离度量的特性

• 最小度量和最大度量代表了簇间距离度量的两个极端。它们趋向对离群点或噪声数据过分敏感。
• 使用均值距离和平均距离是对最小和最大距离之间的一种折中方法，而且可以克服离群点敏感性问题。
• 尽管均值距离计算简单，但是平均距离也有它的优势，因为它既能处理数值数据又能处理分类数据。

纯粹的层次聚类方法的困难之处

• 层次聚类方法尽管简单，但经常会遇到合并或分裂点选择的困难。这样的决定是非常关键的，因为一旦一组对象合并或者分裂，下一步的处理将对新生成的簇进行。
• 不具有很好的可伸缩性，因为合并或分裂的决定需要检查和估算大量的对象或簇。

层次聚类的改进方法

BIRCH (Balanced Iterative Reducing and Clustering using Hierarchies)

Basic Idea

首先用树结构对对象进行层次划分，其中叶节点或者低层次的非叶节点可以看作是由分辨率决定的“微簇”，然后使用其它的聚类方法对这些微簇进行聚类。

BIRCH克服了简单的层次聚类方法的两个缺点：

1. 可伸缩性
2. 不能撤销前一步所做的工作

适用：BIRCH算法比较适合于数据量大，类别数K较多的情况，运行速度快，只需要单遍扫描数据集就能进行聚类。

Method

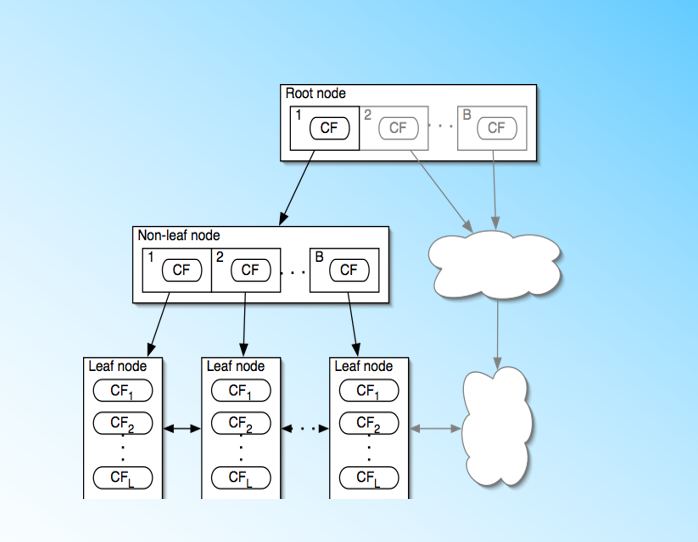
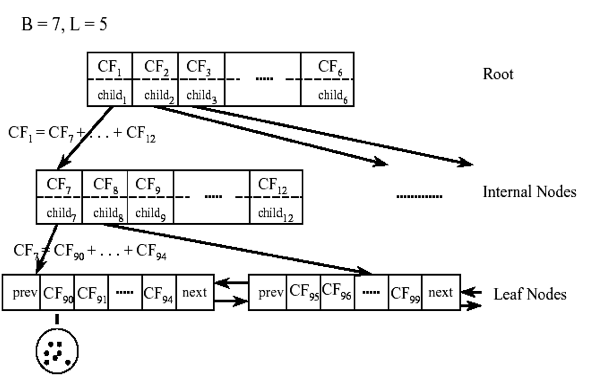
BIRCH算法利用了一个树结构来帮助我们快速的聚类，这个数结构类似于平衡B+树，一般将它称之为聚类特征树(Clustering Feature Tree，简称CF Tree)。这颗树的每一个节点是由若干个聚类特征(Clustering Feature，简称CF)组成。从下图我们可以看看聚类特征树是什么样子的：每个节点包括叶子节点都有若干个CF，而内部节点的CF有指向孩子节点的指针，所有的叶子节点用一个双向链表链接起来。

有了聚类特征树的概念，我们再对聚类特征树和其中节点的聚类特征CF做进一步的讲解。

CF and CF Tree

CF 定义：

每个CF是一个三元组，可以用 (N, LS, SS) 表示。
其中，N代表这个CF中的样本点的数量；LS代表了这个CF中拥有的样本点各特征维度的和向量；SS代表了这个CF中拥有的样本点各特征维度的平方和。
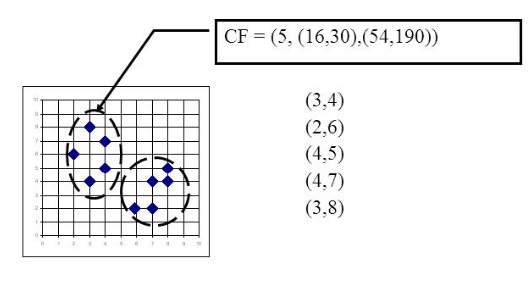
举个例子如下图，在CF Tree中的某一个节点的某一个CF中，有下面5个样本(3,4), (2,6), (4,5), (4,7), (3,8)。则它对应的：
N=5；
LS=(3+2+4+4+3,4+6+5+7+8)=(16,30)；
SS =(32+22+42+42+32+42+62+52+72+82)=(54+190)=244。

CF有一个很好的性质，就是满足线性关系，也就是$C{F}_1+C{F}_2=(N_1+N_2,L{S}_1+L{S}_2,S{S}_1+S{S}_2)$。这个性质从定义也很好理解。如果把这个性质放在CF Tree上，也就是说，在CF Tree中，对于每个父节点中的CF节点，它的(N,LS,SS)三元组的值等于这个CF节点所指向的所有子节点的三元组之和。如下图所示：

从上图中可以看出，根节点的CF1的三元组的值，可以从它指向的6个子节点（CF7 – CF12）的值相加得到。这样我们在更新CF Tree的时候，可以很高效。

对于CF Tree，我们一般有几个重要参数:

1. 每个内部节点的最大CF数$B$
2. 每个叶子节点的最大CF数$L$
3. 第三个参数是针对叶子节点中某个CF中的样本点来说的，它是叶节点每个CF的最大样本半径阈值$T$，也就是说，在这个CF中的所有样本点一定要在半径小于T的一个超球体内。

对于上图中的CF Tree，限定了B=7， L=5， 也就是说内部节点最多有7个CF，而叶子节点最多有5个CF。

CF Tree的生成

下面我们看看怎么生成CF Tree。我们先定义好CF Tree的参数： 即内部节点的最大CF数B， 叶子节点的最大CF数L， 叶节点每个CF的最大样本半径阈值T。

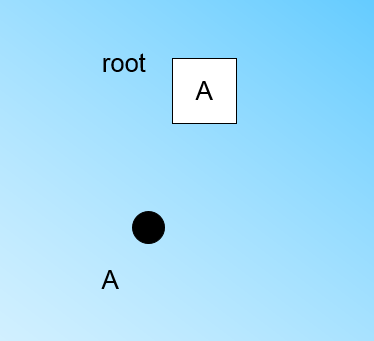
在最开始的时候，CF Tree是空的，没有任何样本，我们从训练集读入第一个样本点，将它放入一个新的CF三元组A，这个三元组的N=1，将这个新的CF放入根节点，此时的CF Tree如下图：

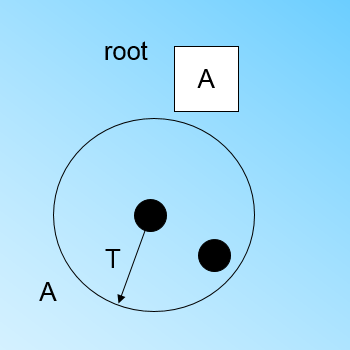
现在我们继续读入第二个样本点，我们发现这个样本点和第一个样本点A，在半径为T的超球体范围内，也就是说，他们属于一个CF，我们将第二个点也加入CF A,此时需要更新A的三元组的值。此时A的三元组中N=2。此时的CF Tree如下图：

此时来了第三个节点，结果我们发现这个节点不能融入刚才前面的节点形成的超球体内，也就是说，我们需要一个新的CF三元组B，来容纳这个新的值。此时根节点有两个CF三元组A和B，此时的CF Tree如下图：

当来到第四个样本点的时候，我们发现和B在半径小于T的超球体，这样更新后的CF Tree如下图：

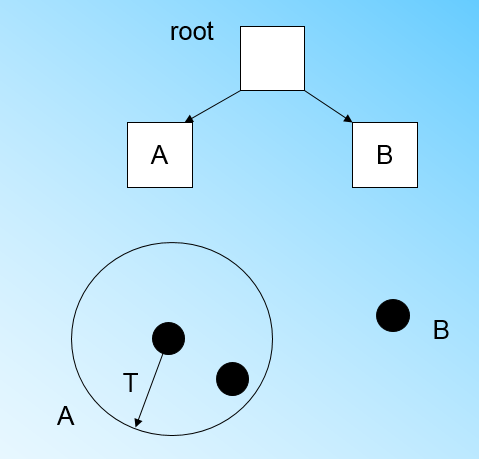
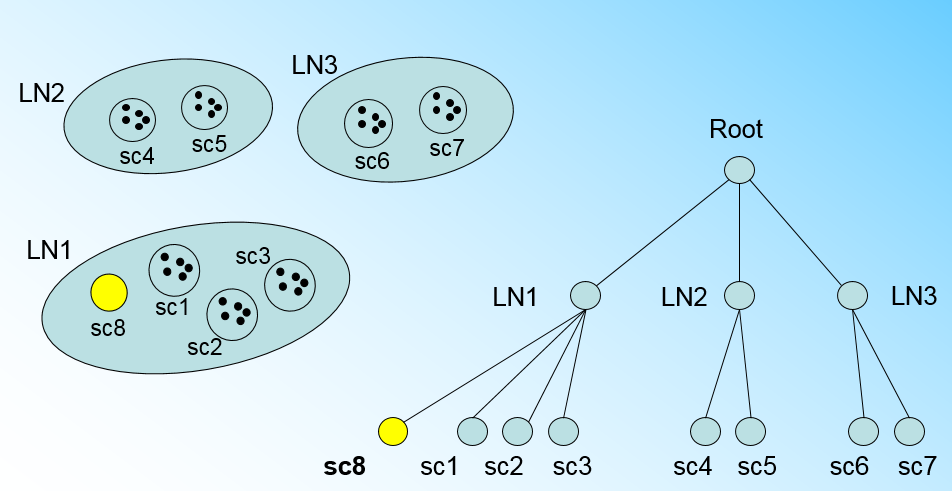
那个什么时候CF Tree的节点需要分裂呢？假设我们现在的CF Tree 如下图， 叶子节点LN1有三个CF， LN2和LN3各有两个CF。我们的叶子节点的最大CF数L=3。此时一个新的样本点来了，我们发现它离LN1节点最近，因此开始判断它是否在sc1,sc2,sc3这3个CF对应的超球体之内，但是很不幸，它不在，因此它需要建立一个新的CF，即sc8来容纳它。问题是我们的L=3，也就是说LN1的CF个数已经达到最大值了，不能再创建新的CF了，怎么办？此时就要将LN1叶子节点一分为二了。

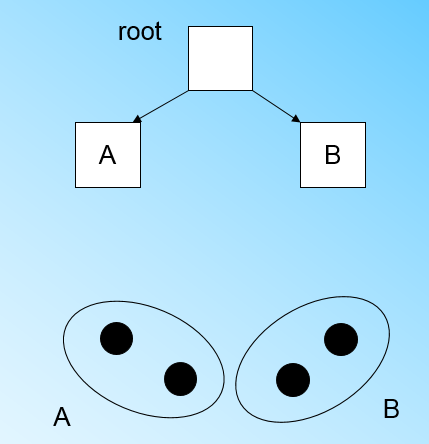
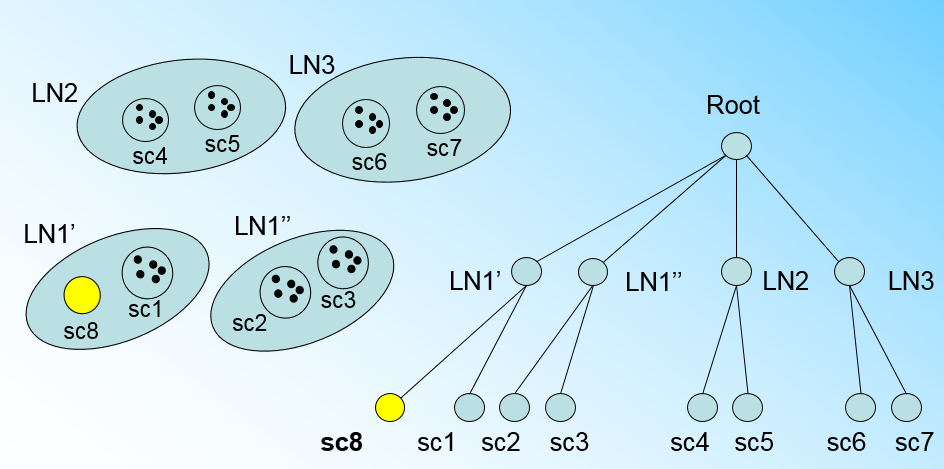
我们将LN1里所有CF元组中，找到两个最远的CF做这两个新叶子节点的种子CF，然后将LN1节点里所有CF sc1, sc2, sc3，以及新样本点的新元组sc8划分到两个新的叶子节点上。将LN1节点划分后的CF Tree如下图：

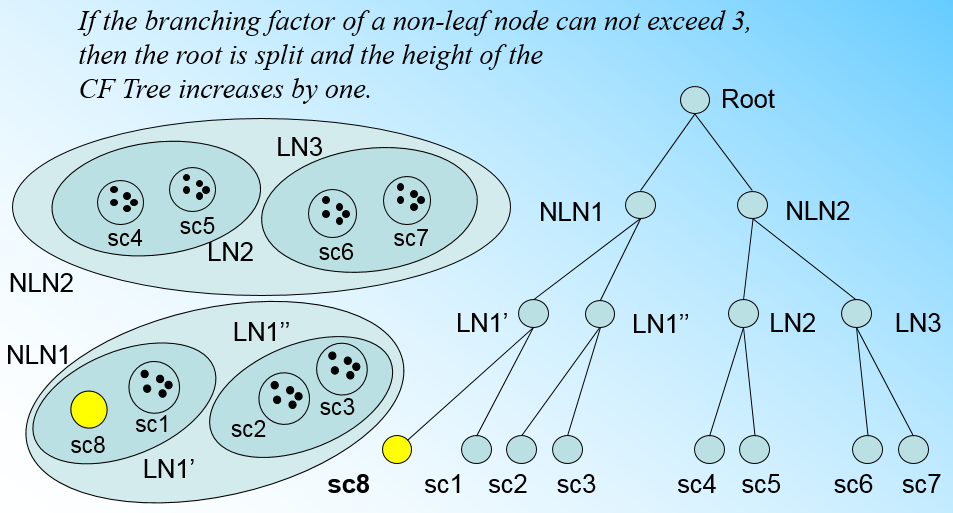
如果我们的内部节点的最大CF数B=3，则此时叶子节点一分为二会导致根节点的最大CF数超了，也就是说，我们的根节点现在也要分裂，分裂的方法和叶子节点分裂一样，分裂后的CF Tree如下图：

有了上面这一系列的图，相信对于CF Tree的插入就没有什么问题了，总结下CF Tree的插入：

1. 从根节点向下寻找和新样本距离最近的叶子节点和叶子节点里最近的CF节点
2. 如果新样本加入后，这个CF节点对应的超球体半径仍然满足小于阈值T，则更新路径上所有的CF三元组，插入结束。否则转入3.
3. 如果当前叶子节点的CF节点个数小于阈值L，则创建一个新的CF节点，放入新样本，将新的CF节点放入这个叶子节点，更新路径上所有的CF三元组，插入结束。否则转入4。
4. 将当前叶子节点划分为两个新叶子节点，选择旧叶子节点中所有CF元组里超球体距离最远的两个CF元组，分布作为两个新叶子节点的第一个CF节点。将其他元组和新样本元组按照距离远近原则放入对应的叶子节点。依次向上检查父节点是否也要分裂，如果需要按和叶子节点分裂方式相同。

BIRCH 算法

上面讲了半天的CF Tree，终于我们可以步入正题BIRCH算法，其实将所有的训练集样本建立了CF Tree，一个基本的BIRCH算法就完成了，对应的输出就是若干个CF节点，每个节点里的样本点就是一个聚类的簇。也就是说BIRCH算法的主要过程，就是建立CF Tree的过程。

当然，真实的BIRCH算法除了建立CF Tree来聚类，其实还有一些可选的算法步骤的，现在我们就来看看 BIRCH算法的流程。

1. 将所有的样本依次读入，在内存中建立一颗CF Tree, 建立的方法参考上一节。
2. （可选）将第一步建立的CF Tree进行筛选，去除一些异常CF节点，这些节点一般里面的样本点很少。对于一些超球体距离非常近的元组进行合并。
3. （可选）利用其它的一些聚类算法比如K-Means对所有的CF元组进行聚类，得到一颗比较好的CF Tree.这一步的主要目的是消除由于样本读入顺序导致的不合理的树结构，以及一些由于节点CF个数限制导致的树结构分裂。
4. （可选）利用第三步生成的CF Tree的所有CF节点的质心，作为初始质心点，对所有的样本点按距离远近进行聚类。这样进一步减少了由于CF Tree的一些限制导致的聚类不合理的情况。

从上面可以看出，BIRCH算法的关键就是步骤1，也就是CF Tree的生成，其他步骤都是为了优化最后的聚类结果。

BIRCH算法的参数：

1. 每个内部节点的最大CF数B （枝平衡因子）。
2. 每个叶子节点的最大CF数L （叶平衡因子）。
3. 每个CF的最大样本半径阈值T （空间阀值T）。

小结

BIRCH算法可以不用输入类别数K值，这点和K-Means，Mini Batch K-Means不同。如果不输入K值，则最后的CF元组的组数即为最终的K，否则会按照输入的K值对CF元组按距离大小进行合并。

一般来说，BIRCH算法适用于样本量较大的情况，这点和Mini Batch K-Means类似，但是BIRCH适用于类别数比较大的情况，而Mini Batch K-Means一般用于类别数适中或者较少的时候。BIRCH除了聚类还可以额外做一些异常点检测和数据初步按类别规约的预处理。但是如果数据特征的维度非常大，比如大于20，则BIRCH不太适合，此时Mini Batch K-Means的表现较好。

对于调参，BIRCH要比K-Means，Mini Batch K-Means复杂，因为它需要对CF Tree的几个关键的参数进行调参，这几个参数对CF Tree的最终形式影响很大。

最后总结下BIRCH算法的优缺点：

BIRCH算法的优点：

1. 节约内存，所有的样本都在磁盘上，CF Tree仅仅存了CF节点和对应的指针。
2. 聚类速度快，只需要一遍扫描训练集就可以建立CF Tree，CF Tree的增删改都很快。
3. 可以识别噪音点，还可以对数据集进行初步分类的预处理。

BIRCH算法的主要缺点有：
4. 由于CF Tree对每个节点的CF个数有限制，导致聚类的结果可能和真实的类别分布不同。
5. 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means。
6. 如果数据集的分布簇不是类似于超球体，或者说不是凸的，则聚类效果不好。

Reference

https://www.cnblogs.com/pinard/p/6179132.html
https://blog.csdn.net/qiu1440528444/article/details/80709663

Reference

python实现一个聚类算法

Clustering by fast search and find of density peaks

2014 Science

工具

PyClustering

官网

sklearn

基于sklearn的聚类算法的聚类效果指标

sklearn 中文教程

Reference

https://blog.csdn.net/xc_zhou/article/details/88316299

知乎：哪种聚类算法可以不需要指定聚类的个数，而且可以生成聚类的规则？

这个写的不错：https://www.cnblogs.com/LittleHann/p/6595148.html

今天的文章clustering 聚类算法分享到此就结束了，感谢您的阅读。