圆形的面积怎么算_圆表面积「建议收藏」

人教版是从生活情境提出圆面积的概念，体会在实际生活中计算圆面积的必要性。学生以前学过的图形都是多边形(如三角形、长方形、正方形、平行四边形和梯形等)，都是直边图形，像圆这样的曲线图形的面积计算，学生还是第一次接触到，理解起来比较困难。教材直接给出明确的提示，让把圆平均分成若干等份，拼一拼。教师把重点放在了拼和拼后找关系上，忽略了圆的面积的转化过程，求圆的面积人类经过了漫长的过程，其中中国数学家刘徽的“割圆术”以出入相补的归纳思想计算圆的面积，和西方的欧几里得的演绎风格迥然不同却相辅相成。现在的问题是，怎样才能让学生在简单经历割圆术的思想方法的基础上想到如何进行剪拼。我们在人教版、青岛版、北师大版教材上都能看到“割圆术”的影子，怎样在求圆的面积时从这个角度进行教学呢？

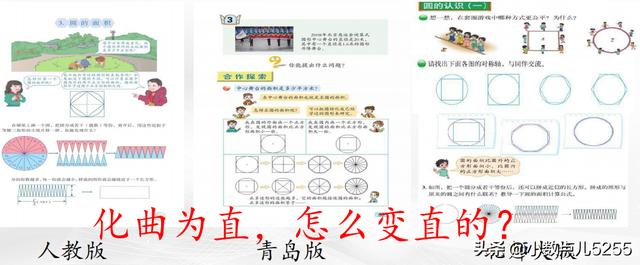
我们可以尝试这样引导：师：怎样计算圆的面积呢？

生：转化成已经学过的图形。

师：可圆是曲线图形，不能直接转化成学过的图形，怎么办呢？

生：……

师：虽然不能直接转化，我们可以用学过的图形进行研究，比如我们在圆内画一个最大的正方形，这个正方形的面积和圆的面积比较？

生：圆的面积大于里面正方形的面积。

师：这一点我们在圆的认识时就知道了，而且还知道……？

生：圆的面积小于外接正方形的面积。

师：如果内接和外接的正多边形边越多，我们会发现？

课件出示，生：最后和圆重合，就是圆的面积。

师：我们试着把圆分割一下，正方形的时候分割成了四个扇形，随着正多边形的边数不断增多，把圆分割成了很多什么图形？

生1：小三角形，生2：终于分成了学过的图形。

师：正多边形的边数越多，越接近三角形，把这些三角形取下来拼一拼看看你们能发现什么？

……

事实上，把圆转化成直边图形单靠学生主动探究是很难实现的，从极限的角度他们是很难跨过这个思想鸿沟的，即使按照上述的方法引导有意识的，能朝着正确的方向去做，但最后也会因为数量和表象达不到效果，或者从宏观上解释：是现实操作与理想数学之间的冲突导致的难以持续研究。所以我认为，圆的面积是前面平面图形面积教学的一次全面提升，它应该是让学生经历和掌握圆面积公式的由来，更重要的是体会，平面图形间从“无限”的角度能够实现转化，以及了解有关圆的历史探究知识，在思维上是一次飞跃。(化曲为直、怎么变直的？变直的过程是课堂上研究的重点)

最早计算圆面积的是中国数学家刘徽，距离我们近二千年，比祖冲之稍早一些，他写的一本数学著作《九章算术》。刘徽最突出的数学成就就是“割圆术”，祖冲之就是利用刘徽的割圆术发现圆周长与直径的比值是3倍多一些，方便我们计算圆的周长。而刘徽利用割圆术发现圆面积的计算方法，面积的计算公式是刘徽的贡献。他把圆分割为若干小扇形，他从正六边形出发，将边数逐次加倍，并逐步计算正多边形的面积。他说“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失”。圆面积的计算还表现刘徽另一数学原理“出入相补”：一个几何图形被分割为若干后，面积或体积保持不变。此时刘徽已有极限思想。

史宁中教授指出，数学最上位的思想主要是归纳和演绎，“几何测量”教学中，教学的主体思想不应该忽视演绎推理，那就是重视让学生经历公式(算法)的形成过程。