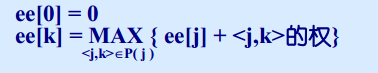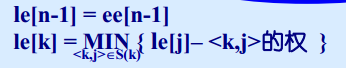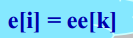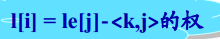AOV网的定义
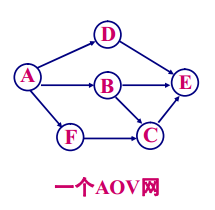
以顶点表示活动,以有向边表示活动之间的优先关系的有向图称为顶点表示活动的网(Activity On Vertex Network),简称AOV网,如下:
在AOV网中,若顶点i到顶点j之间有路径,则称顶点i为顶点j的前驱,顶点j为顶点i的后继;
若顶点i到顶点j之间为一条有向边,则称顶点i为顶点j的直接前驱,顶点j为顶点i的直接后继
在AOV网中,最重要的两个知识点就是拓扑排序和关键路径,其中拓扑排序用于判断AOV网中是否存在回路,有回路则活动永远也结束不了,关键路径可以得出关键活动以及完成整个活动的最短时间,下面分别介绍这两个知识点。
拓扑排序
检测工程能否正常进行,首先要判断对应的AOV网中是否存在回路,达到该目的最有效的方法之一是对AOV网构造其顶点的拓扑序列,即对AOV网进行拓扑排序
什么是拓扑排序?
拓扑排序在离散数学中的定义如下:
由某个集合上的一个偏序得到该集合上的一个全序的操作称为拓扑排序;
是不是有些难以理解?忽略上述定义,看如下更易懂的定义:
构造AOV网的一个顶点序列,使得该顶点序列满足下列条件:
1、若在AOV网中,顶点i 优先于顶点j,则在该序列中顶点i 仍然优先于顶点j;
2、若在AOV网中,顶点i 与顶点j之间不存在优先关系,则在该序列中建立它们的优先关系,即顶点i优先于顶点j,或者顶点j 优先于顶点i;
3、若能构造出这样的拓扑序列,则拓扑序列包含AOV网的全部顶点,说明AOV网中没有回路;若构造不出这样的序列,说明AOV网中存在回路
拓扑排序的核心思想
拓扑排序的核心思想如下:
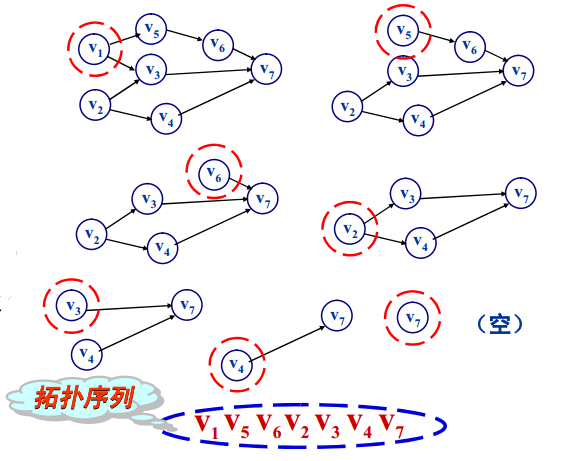
1、 从AOV网中任意选择一个没有前驱的顶点;
2、 从AOV网中去掉该顶点以及以该顶点为出发点的所有边;
3、 重复上述过程,直到AOV网中的所有顶点都被去掉(AOV网中无回路),或者AOV网中还有顶点,但不存在入度为0 的顶点(AOV网中存在回路)。
上述方法的图示如下:
注:拓扑序列不一定唯一;
用堆栈实现拓扑排序算法
AOV图采用邻接表存储方式,使用堆栈实现拓扑排序的算法步骤如下:
1、首先建立一个入度为0的顶点堆栈,将网中所有入度为0的顶点分别进栈;
2、当堆栈不空时,反复执行以下动作:
2.1、从顶点栈中退出一个顶点,并输出它;
2.2、从AOV网中删去该顶点以及以它发出的所有边,并分别将这些边的终点的入度减1;
2.3、若此时边的终点的入度为0,则将该终点进栈;
3、若输出的顶点个数少于AOV网中的顶点个数,则报告网中存在回路,否则,说明该网中不存在回路;
Q:除了进行拓扑排序,还可以采用什么方法判断一个有向图是否存在回路?
A:还可以对AOV网图进行深度优先遍历。若从某个顶点v出发,遍历结束前出现了从顶点u到顶点v的回边,则可以断定图中包含顶点v到顶点u的回路。(广度优先不可以)
AOE网的定义
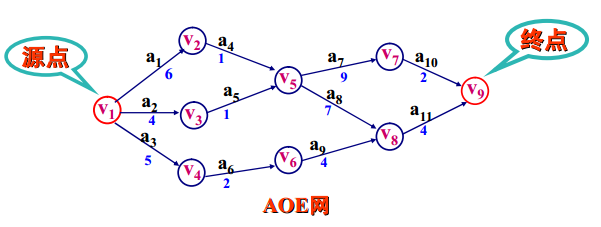
AOE(Activity On Edge)网为一个带权的有向无环图,其中,以顶点表示 事件,有向边表示 活动 ,边上的权值表示活动持续的时间 ,如下图:
1、正常情况下,AOE网中只有一个入度为0的顶点,称之为 源点;有一个出度为0 的顶点,称之为 终点;
2、只有在某个顶点所代表的事件发生以后,该顶点引发的活动才能开始;
3、进入某事件的所有边代表的活动都已完成,该顶点代表的事件才能发生;
关键路径
关键路径的定义和特点
从源点到终点的路径中具有最大长度的路径为关键路径;关键路径上的活动称为关键活动。
关键路径的特点:
1、关键路径的长度(路径上的边的权值之和)为完成整个工程所需要的最短时间;
2、关键路径的长度变化(即任意关键活动的权值变化)将影响整个工程的进度,而其他非关键活动在一定范围内的变化不会影响工期;
关键路径算法
核心思想:
1、e[i] — 活动ai的最早开始时间;
2、l[i] — 活动ai的最晚开始时间;
若l[i]–e[i]=0,则说明活动ai为一个关键活动;所有的关键活动连接起来即为关键路径;
注:活动指的是AOE网络中的边;事件指的是AOE网络中的结点;
对于事件和活动,有如下结论:
事件k的最早发生时间ee[k] = 活动的ai最早开始时间e[i];
事件k的最晚发生时间le[k] = 活动的ai最晚开始时间l[i];
求关键路径的步骤
AOE图使用邻接矩阵的存储方式
求关键路径的步骤如下:
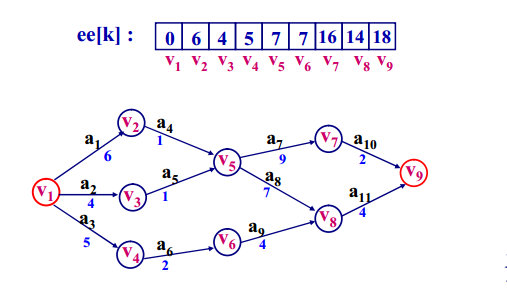
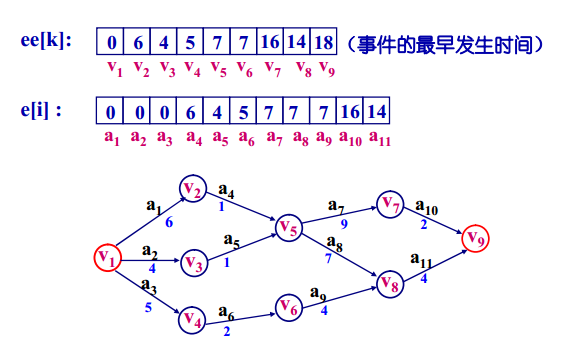
1、计算事件k的最早发生时间ee[k]
事件k的最早发生时间决定了由事件k出发的所有活动的最早开始时间;该时间是指从源点到顶点(事件)k的最大路径长度,计算方法如下图:
样例如下:
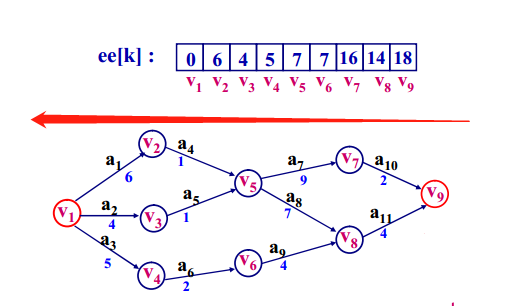
2、计算事件k的最晚发生时间le[k]
所谓事件k的最晚发生时间是指不影响整个工期的前提下事件k必须发生的最晚时间,它必须保证从事件k发出的所有活动的终点事件的最迟发生时间,该过程是一个从终点到源点的反推计算过程,计算方法如下:
样例如下:
3、计算活动 i 的最早开始时间e[i]
所谓活动i的最早开始时间实际上是事件k发生的最早时间,即只有事件k发生,活动i才能开始,计算方法如下:
样例如下:
4、计算活动 i 的最晚开始时间l[i]
所谓活动i的最晚开始时间是指不推迟整个工期的前提下活动i开始的最晚时间,计算方法如下:
样例如下:
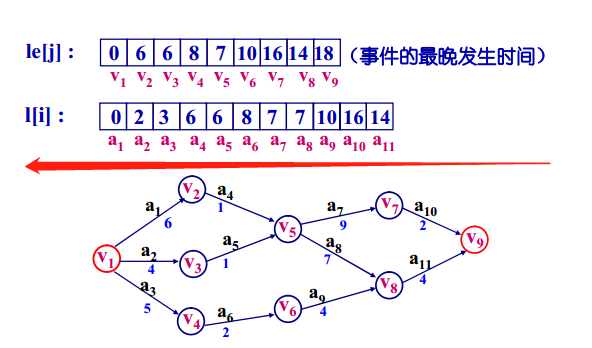
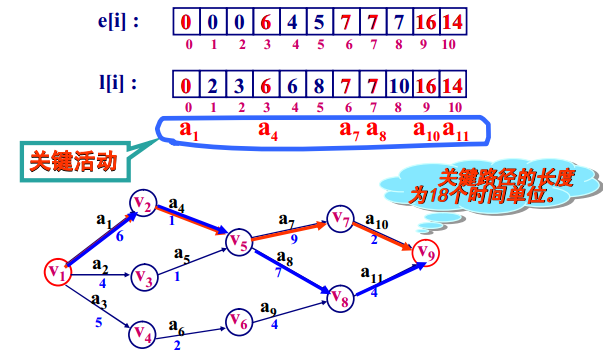
5、求出关键活动与关键路径
找出所有l[i] = e[i] 的活动,则这些关键活动组成关键路径,如下:
今天的文章aov网的拓扑序列_树形网络拓扑图「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/88659.html