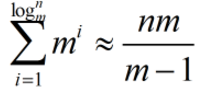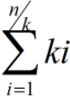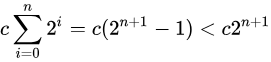vector扩充容量_id4热成型钢板比例

我们知道，vector 在插入新的元素时但是之前的内存已经满的时候需要扩容，在 VS 下是 1.5倍，在 GCC 下是 2 倍。那么会产生两个问题：
（1）为什么是成倍增长，而不是每次增长一个固定大小的容量呢？
（2）为什么是以 2 倍或者 1.5 倍增长，而不是以 3 倍或者 4 倍等增长呢？

1、第一个问题 ：
如果以成倍方式增长
假定有 n 个元素,倍增因子为 m； 完成这 n 个元素往一个 vector 中的 push_back​操作，需要重新分配内存的次数大约为logm(n)，就是说如果这n个元素都需要扩容才可以加入，那么最坏的情况下也是需要分配内存的次数是logm(n)；
第 i 次重新分配将会导致复制 m^(i) (也就是当前的vector.size() 大小)个旧空间中元素; n 次 push_back 操作所花费的时间复制度为O(n)，如下图所示：

m / (m – 1)，这是一个常量，均摊分析的方法可知，vector 中 push_back 操作的时间复杂度为常量时间.​

但是如果一次增加固定值大小
假定有 n 个元素,每次增加k个；第i次增加复制的数量为为：100i ；n 次 push_back 操作所花费的时间复杂度为O(n^2):

均摊下来每次push_back 操作的时间复杂度为O(n)；
总结对比
可以发现采用采用成倍方式扩容，可以保证常数的时间复杂度，而增加指定大小的容量只能达到O(n)的时间复杂度，因此，使用成倍的方式扩容。

2、第二个问题

有人回答说：vector最关键在于查询，使用移位（2的幂）直接得到哈希链以及节点长度，然后相减直接得到键值，复杂度为O(2)，性能近似于数组，插入删除可动态，这就是vector设计的基本目的。

显然，增长的倍数不可能很大，也不会比 1 小，那么，它的最佳上限是多少呢？如果以 大于2 倍的方式扩容，下一次申请的内存会大于之前分配内存的总和，导致之前分配的内存不能再被使用。所以，最好的增长因子在 （1,2）之间。

知乎上有这样一段解释：
C++ STL中vector内存用尽后，为啥每次是两倍的增长，而不是3倍或其他数值？

使用 k=2 增长因子的问题在于，每次扩展的新尺寸必然刚好大于之前分配的总和：

也就是说，之前分配的内存空间不可能被使用。这样对于缓存并不友好。最好把增长因子设为 1 < k < 2

当 k =1.5 时，在几次扩展以后，可以重用之前的内存空间了
以上内容转自：
STL vector(四) vector 扩容为什么要以1.5倍或者2倍扩容

至于为什么当k = 1.5的时候可以重用之前的内存空间呢？博主并没有做出详细的解释
我看了上面提到的知乎那篇问答中也有好多朋友在问知乎的那位大神这个问题（我在此再次膜一下^ – ^），当然也有好多dalao在盖楼解答，开始的时候不是很理解，多次阅读后我谈一下自己的理解：
这个和等比数列的概念有关：
我们知道等比数列的第n项的通项公式：an=a1*q^(n-1)
前n项和公式是：Sn = a1*(1-q^n)/(1-q)
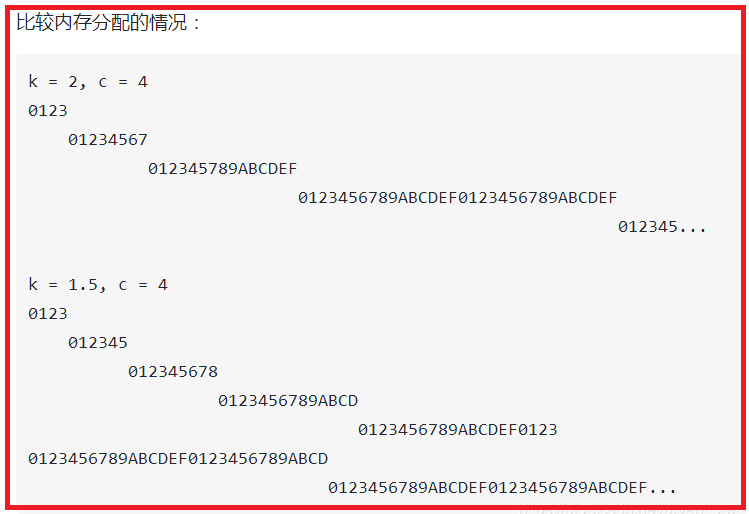
就还用上面的红色框中的图片说说：c = 4

• 当k = 2时:
  第n次扩容的时候需要分配的内存是：an = a1*q^(n-1) = 4*2^(n-1)
  而前n-1项的内存和为：Sn = a1*(1-q^(n-1))/(1-q) = 4*(1-2^(n-1)) /(1-2) = 4*2^(n-1)-4

  差值 = an - Sn = 4 > 0
  

  所以第n次扩容需要的空间恰好比前n-1扩容要求的空间总和要大，那么即使在前n-1次分配空间都是连续排列的最好情况下，也无法实现之前的内存空间重用

• 当k = 1.5时:

  第n次扩容的时候需要分配的内存是：an = a1*q^(n-1) = 4*1.5^(n-1)
  而前n-1项的内存和为：Sn = a1*(1-q^(n-1))/(1-q) = 4*(1-1.5^(n-1)) /(1-1.5) = 8*1.5^(n-1)-8

  差值 = an - Sn = 8 - 4*1.5^(n-1)
  当n增长到一定的数值后，差值就会变为小于0，此时便可以实现内存空间复用
  

今天的文章vector扩充容量_id4热成型钢板比例分享到此就结束了，感谢您的阅读。