《C语言》字符串匹配（BF算法+KMP算法）

字符串匹配

【问题描述】
对于字符串S和T，若T是S的子串，返回T在S中的位置（T的首字符在S中对应的下标），否则返回-1.

【问题求解】

● ㈠ BF算法

该直接穷举算法从字符串S的每一个字符开始查找，看字符串T是否会出现。
第一步：把T[0] 跟S [0] 匹配，如果相同则匹配下一个字符；
第二步：当出现字符不相同，丢弃前面的已匹配信息 ，T[1] 跟 S[0]匹配，循环进行，直到主串结束，或者出现匹配成功的情况。
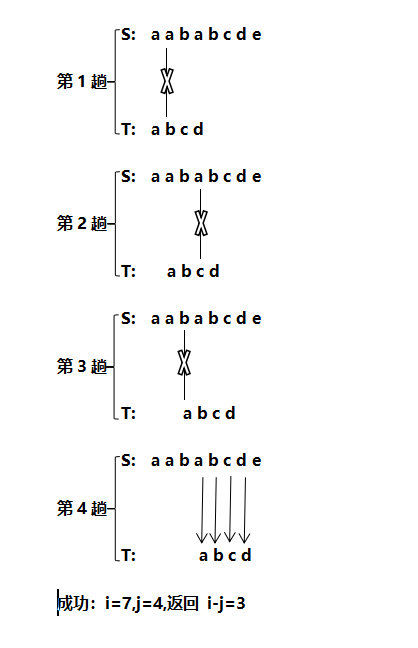
例如：S=“aababcde”,T=“abcd”；过程如下：

【BF算法代码】

#include<stdio.h> 
#include<string.h>
int BF(char s[],char t[])  //字符串匹配
{ 
    int i=0,j=0;
while (i<strlen(s)&&j<strlen(t))
{ 
   
	if(s[i]==t[j]){ 
           //比较两个字符串相同时 
		i++;
		j++;
	}
	else{ 
                     //比较两个字符串不相同时 
		i=i-j+1;           //i回退到原来i的下一个位置 
		j=0;               //j从0开始 
	}
 }
 if(j==strlen(t))          //t的字符比较完毕 
    return i-j;            //t是s的子串，返回位置 
 else                      //t不是s的子串 
    return -1;             //返回-1 
}
int main(){ 
   
	char S[]="abaacababcac";
	char T[]="ababc";
	printf("T在S中出现的起始位置： %d\n",BF(S,T));
}

【程序结果】

★时间复杂度：O（n*m）.
☆算法缺陷：丢弃前面的匹配信息的方法，极大地降低了匹配效率。

● ㈡ KMP算法

〖定义〗：Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串T 的出现位置。
〖算法描述〗：

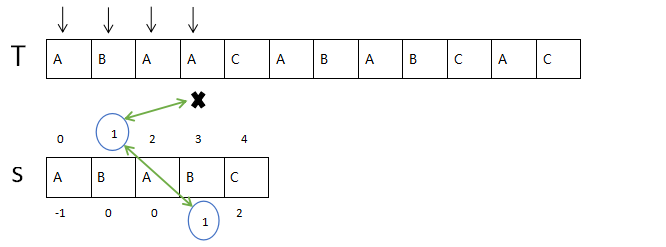
设主串T为：A B A A C A B A B C A C

模式串S为：A B A B C

第一次匹配
设主串T为：A B A A C A B A B C A C

模式串S为：A B A B C

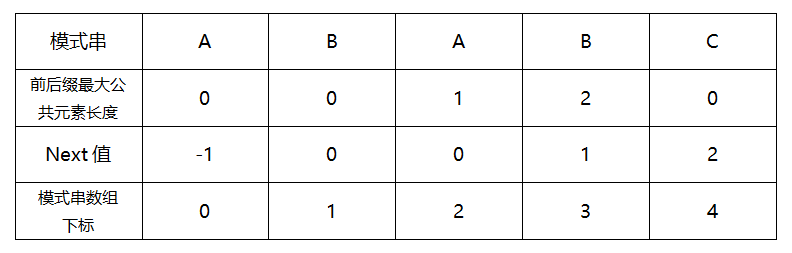
①寻找前缀后缀最长公共元素长度 .
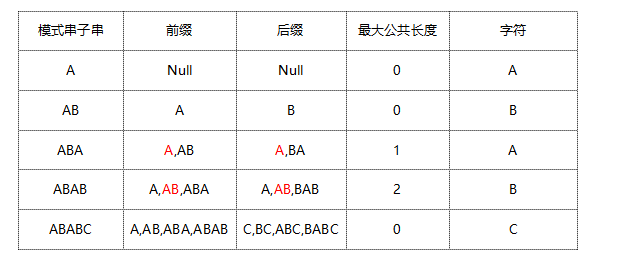
由于T[3]≠S[3]，而T[0] ~T[2]相同；则移动找出最长的相同的前缀和后缀并使他们重叠，计算过程和方法如下表格所示：

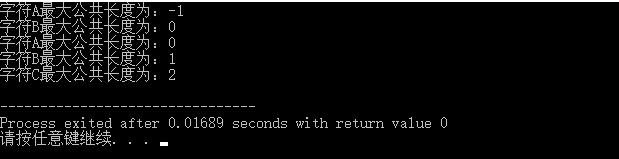
[程序思想举例]：
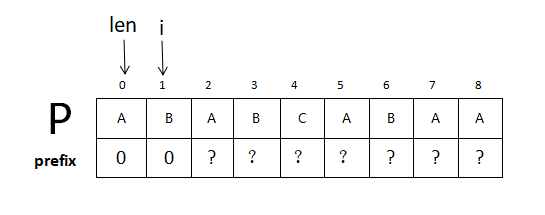
<1>.len和i为用来比较的变量，pattern[i] == pattern[len]，len++，prefix[i]=len的值，prefix[i] = len的值，i继续向下比较。

<2>.当pattern[i] ≠pattern[len]时，且len>0的情况下，向左逐次移动，再次进行循环比较，可计算得A代表的公共长度为1；直至结束即可

【算法代码①】
注：prefix_table（前缀后缀最长公共元素长度表）

void prefix_table(char pattern[],int prefix[],int n){ 
    //1.要匹配的子串表，2.前缀表，3.表长 
	 prefix[0] = 0;	            //定义第一个字符最长公共长度为0；
	 int len = 0;               //用来比较的长度
	 int i   = 1;
	 while(i<n){ 
   
	 	if(pattern[i] == pattern[len]){ 
   
	 		len++;
	 		prefix[i] = len;
	 		i++;
		 }else{ 
                             //当pattern[i]≠pattern[len]时
		 	if(len > 0){ 
                     //避免向左校对时出界
		 		len = prefix[len - 1];    
		 }else{ 
                              
		 	prefix[i]=len;
		 	i++;
		 }
	   }
    } 
}

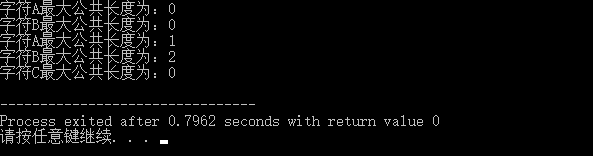
【程序结果】

②求next数组.
next 数组考虑的是除当前字符外的最长相同前缀后缀，所以通过第①步骤求得各个前缀后缀的公共元素的最大长度后，只要稍作变形即可：将第①步骤中求得的值整体右移一位，然后初值赋为-1，如下表格所示：

【算法代码②】
注：Next（前缀移动方法）

void Next(int prefix[],int n){ 
     //前缀表移动 
	int i;
	for(i=n-1;i>0;i--){ 
   
		prefix[i]=prefix[i-1];
	}
	prefix[0]=-1;
}

【程序结果】

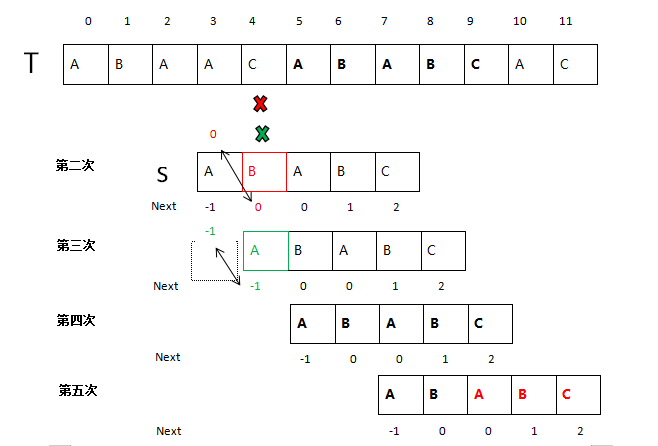
③根据next数组继续进行匹配.
<1>. 根据第一次匹配分析，当T[3]≠S[3],字符B对应的Next值=1，即移动S子串，S[1]移动于T[3]下，继续进行匹配；

<2>.当S[1]≠T[4]时，字符B对应的Next值=0，即将S[0]移动于T[4]下匹配；
<3>.当S[0]≠T[4]时，字符A对应的Next值=-1，即将虚拟的S[-1]向右移一位至T[4]下，等价于S[0]移动于T[5]下匹配；
<4>.匹配成功，继续寻找；匹配成功的最后一位字符C对应的Next值=2，把对应的S[2]移动于T[9]下匹配；
<5>.匹配结束；返回子串对应的起始位置：5。
匹配过程和方法表如下：

【KMP算法代码】

注==：完整算法代码

#include<stdio.h>
#include<malloc.h>
#include<string.h>
void prefix_table(char pattern[],int prefix[],int n){ 
    //1.要匹配的子串表，2.前缀表，3.表长 
	 prefix[0] = 0;	   //定义第一个字符最长公共长度为0； 
	 int len = 0;      //用来比较的长度
	 int i   = 1;
	 while(i<n){ 
   
	 	if(pattern[i] == pattern[len]){ 
   
	 		len++;
	 		prefix[i] = len;
	 		i++;
		 }else{ 
   
		 	if(len > 0){ 
                   //避免向左校对时出界
		 		len = prefix[len - 1];  //当pattern[i]≠pattern[len]时
		 }else{ 
   
		 	prefix[i]=len;
		 	i++;
		 }
	   }
    } 
}

void Next(int prefix[],int n){ 
     //前缀表移动 
	int i;
	for(i=n-1;i>0;i--){ 
   
		prefix[i]=prefix[i-1];
	}
	prefix[0]=-1;
}

void kmp_search(char text[],char pattern[]) { 
     //text为母表，patter为子表
	int n=strlen(pattern);
	int m=strlen(text);
	int* prefix=(int*)malloc(sizeof(int)*n);  //创建数组
	prefix_table(pattern,prefix,n);
	Next(prefix,n);
	
	//text[i] 定位表示 len(text) =m
	//pattern[j], 定位表示len(pattern )= n 
	int i=0;
	int j=0;
	while(i<m){ 
   
		if(j == n-1 && text[i] == pattern[j]){ 
   
			printf("子串匹配于母串起始位置： %d\n",i-j);
			j=prefix[j];
		}
		if(text[i] == pattern[j]){ 
   
			i++;
			j++;
		}else{ 
   
			j=prefix[j];
			if(j==-1){ 
   
				i++;
				j++;
			}
		}
	}
}

int main(){ 
   
	char pattern[]="ABABC";
	char text[]   ="ABAACABABCAC";
	kmp_search (text,pattern);
	return 0;
} 

【算法结果】

★时间复杂度：O（n+m）.

假如李白会编程，夸张字符随意配；暴力美学最简易，KMP经典最美丽。

今天的文章《C语言》字符串匹配（BF算法+KMP算法）分享到此就结束了，感谢您的阅读。