Matlab拟合——Curve Fitting工具

这两天也简单地用了matlab去拟合离散数据，感觉还是非常方便的。这里记录一下自己使用matlab拟合的流程，也希望你太清楚matlab拟合用法的小伙伴能有所收获。

1 打开工具

打开matlab，点击左上角的APP，找到Curve Fitting工作（当然打开它的方式有很多，不做展开）。

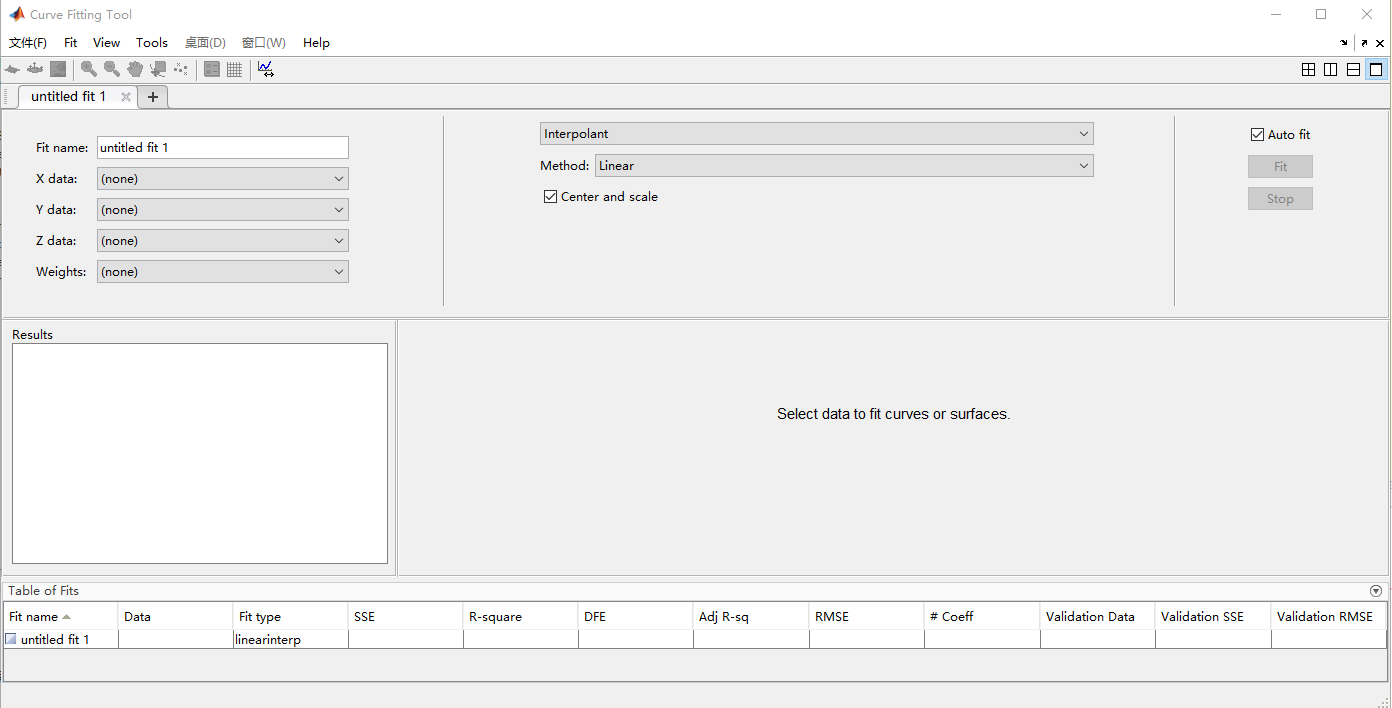
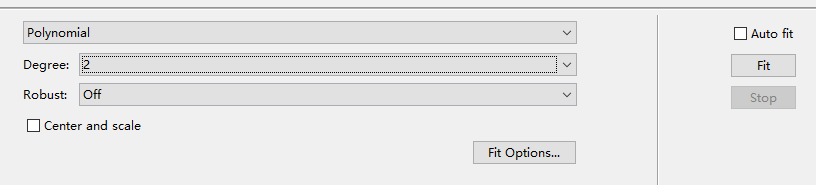
打开以后的窗口如图

这个窗口里有的选项也是超级多，但我会得不多，只是去摸索了一些够自己用的东西。

2 用函数表达式拟合数据

拟合数据前，肯定是要先有数据，因此咱们先做点数据。

x = 1:0.2:4;
y = x.^2 + rand(1,size(x,2));
plot(x,y,'+');

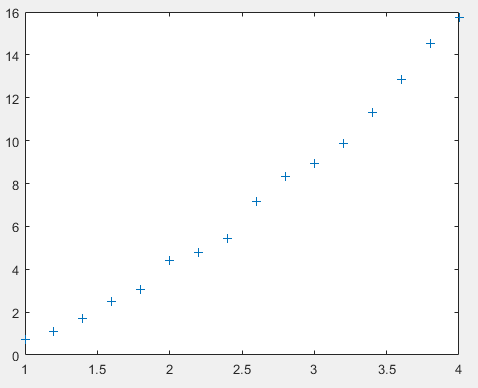
(x,y)就是我们创建的离散数据，数据的分布如下图：

因为加入了噪声，所以数据点的形状存在一些波动。那么现在用Curve Fitting工具来对这些离散数据做拟合。打开Curve Fitting工具，看到窗口的左边有【Fit name】、【X data】、【Y data】、【Z data】等等东西（我没有写的东西不是我忘写了，是我也不知道是干啥的）。

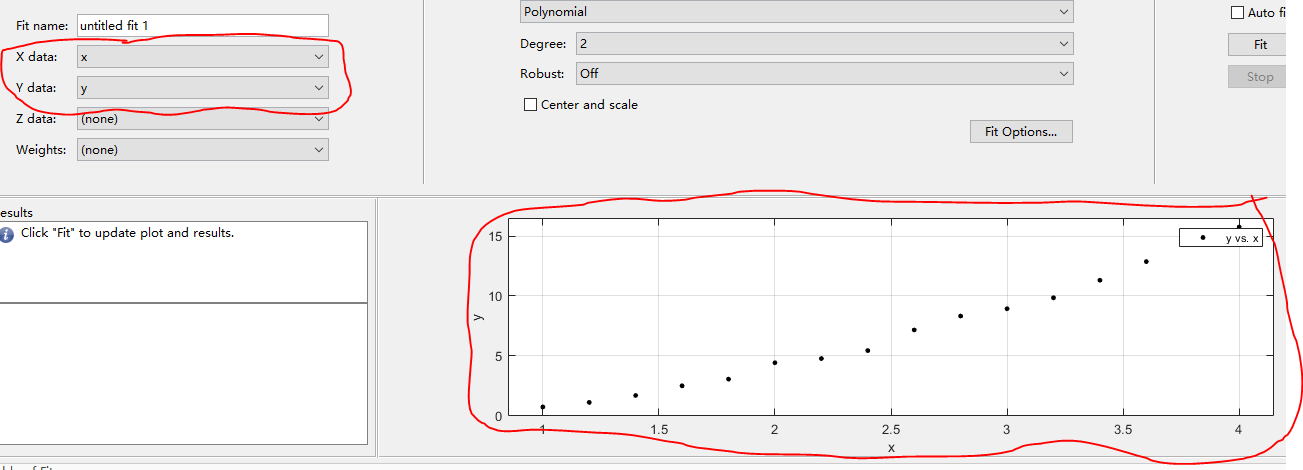
主要来看【X data】和【Y data】，这里是要输入要拟合的离散数据，那么【X data】就选刚刚创建的x序列，【Y data】就选刚刚船舰的y序列，画面上就会出现这些数据的分布了，如下图

然后看到窗口的中上部分，这里可以选择拟合的方式，关于拟合方式的详细介绍，大家可以看这篇文章，因为是人家整理的东西，我也不好直接复制过来。

各种拟合方式说明

这里，我们希望它能拟合成一个二次函数，所以选择【Polynomail(多项式拟合)】，【Degree（阶数）】选择为2，然后点击窗口右边的【fit】，就得到拟合的函数曲线和拟合的参数了。

拟合完以后，窗口上会显示的东西有，1）拟合的曲线；2）拟合后的参数；3）拟合误差的评估，如下图

可以看到（可能看不到，我图片都是复制的，不是导入的，应该巨糊……），给出的拟合结果是
f(x) = p1x^2 + p2x + p3，
p1 =0.8882 ，p2 =0.6097 ，p3 = -0.8021

这个拟合结果很垃圾，我们希望的结果应该是p1接近1，而p2和p3接近0。那么为什么会这样呢？首先第一个原因当然是因为加入了噪声的干扰，使得数据有偏差。其次，数据点太少了。

既然如此，那么就增多数据点，将x=1:0.2:4;改为x=1:0.01:4；数据一下增加了好多倍，而得到的拟合结果如下：

拟合的结果是
f(x) = p1x^2 + p2x + p3，
p1 = 1.035，p2 = -0.2087，p3 =0.261

这个结果虽然还有不足，但比起第一次的结果又好很多了。那还有什么问题造成拟合效果不好呢？就是x的范围太小了，只有[1,4]，如果增加x的取值范围，那么拟合效果又会进一步提升。

上述只是一个很简单的例子，除了多项式拟合，这个工具还有很多其他的拟合方式，大家都可以尝试一下。

3 拟合设置

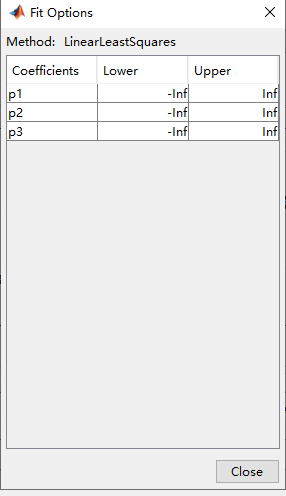
在窗口的中上位置，有一个【Fit Options】的按钮，点击它，就可以对拟合过程进行一些设置。

我们上个例子是一个很简答的拟合过程，因此这里的拟合设置，可以控制的量也比较少，只有拟合参数的Lower(上限)和Upper(下限)设置。有些拟合方式还有又拟合参数的初值设置。有时候，设置一个好的处置和上下限，可以让拟合的结果收敛得更好。

这里只是和大家提一下有这个【Fit Options】设置，详细内容我知道也不多，就不展开了。

4 自定义函数拟合

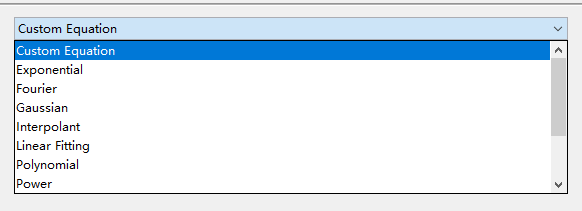
在窗口得中上位置，选择拟合方式这里，可以选择【Custom Equation】，这个表示得是用户自定义一个函数进行拟合。

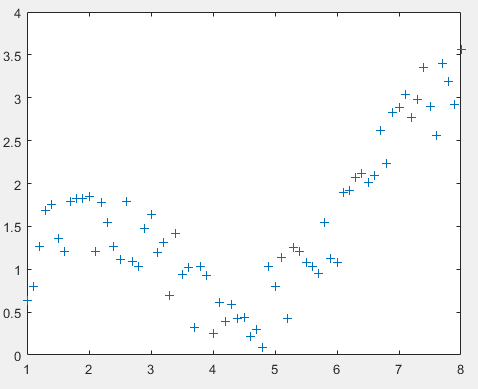
我们先生成一些离散样本，这里，我们生成得样本y是一个Curve Fitting工具里面没有得一个拟合函数，离散样本的分布如下图。

x = 1:0.1:8;
y = sin(x)+log(x)+rand(1,71)-0.5;
plot(x,y,'+');

我透，加了这个噪声以后，这啥也不是。不过好在我们知道我们要拟合的函数时什么样的。

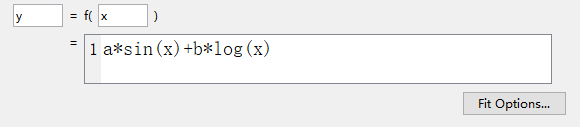
选择【Custom Equation】的拟合方式，自定义一个拟合函数，如下图：

我们定义的拟合函数是f(x)=asinx+blogx，这里的a与b就是拟合工具要给我们拟合出来的参数。

点击右侧的【Fit】，就可以得到拟合的曲线和拟合的参数了，如下图：

拟合的结果为：
f(x) = asin(x)+blog(x)
a=1.061，b=1.029。

哦哟，拟合的效果竟然这么好？

5 无函数表达式的插值拟合

有些时候我们并不是需要一个准确的函数表达式，只是想由这些离散的数据，得到一个平滑的连续的曲线，那这时候可以用”插值“的方式来实现。

比如一个温度曲线，它是没有准确的函数表达式的，就是很多零散的观测点，而通过插值，我们可以得到哪些出在观测时间点中间时候的温度情况。

自行拟定一个温度的序列

x = 1:10;
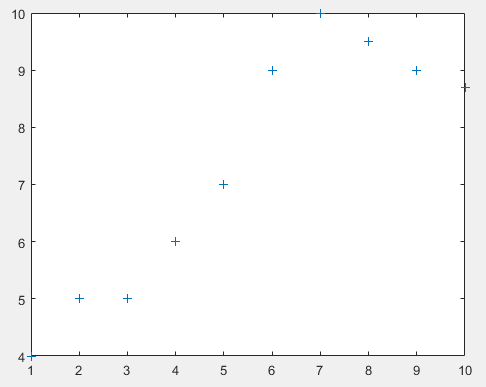
y = [4,5,5,6,7,9,10,9.5,9,8.7];
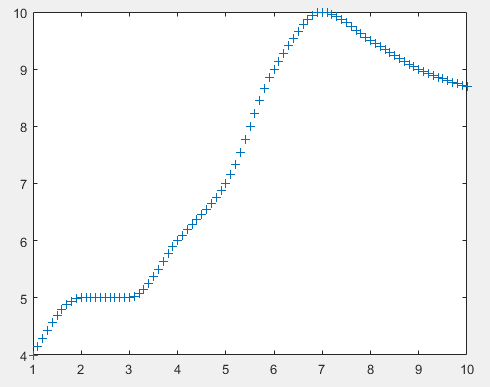
plot(x,y,'+');

这是一个温度变化的曲线，没有很准确的函数表达式，我们现在就是想通过插值拟合的方式，推测不是整点时间点的温度。

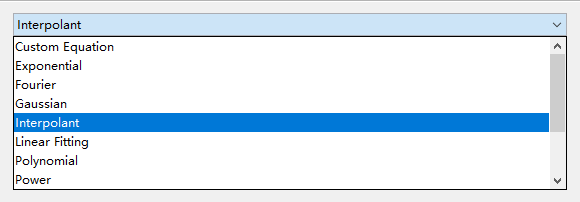
选择拟合方式为【Interpolant】

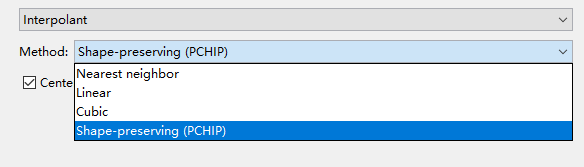
在下栏的【Method】还可以选择插值的方式，这个我具体就不做展开了。这里我们选择【Shape-preserving(PCHIP】。

点击右侧的【Fit】，就得到了拟合的曲线。这种拟合方式是没有函数表达式的，因此没有拟合的参数。

6 导出拟合函数（拟合关系）

前面讲了3个例子，1）用一个二次多项式拟合；2）设置一个自定义函数去拟合；3）用插值的方式拟合了一条连续的曲线。

对于前两个，由于拟合的是有确定表达式的函数，在我们获得拟合参数以后，我们可以把这些参数套到函数里面去，就想怎么用就怎么用了。但对于第三种，它没有函数表达式，我们虽然拟合出来一个很好看的曲线，但用不上，怎么办呢？

其实，不管有没有函数表达式，拟合出来的拟合关系都是可以导出使用的。

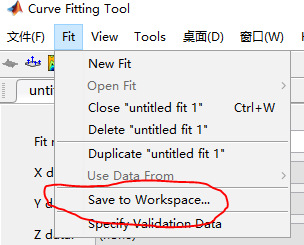
当我们拟合出了一条曲线以后，点击Curve Fitting窗口右上角的【Fit】-【Sava to Workspace】


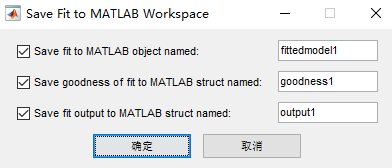
上图的三个选项种，第一个表示导出拟合函数（拟合关系），剩下两个我没去研究过，就不做展开了。点击确定以后，拟合函数（拟合关系）就保存到工作区了。

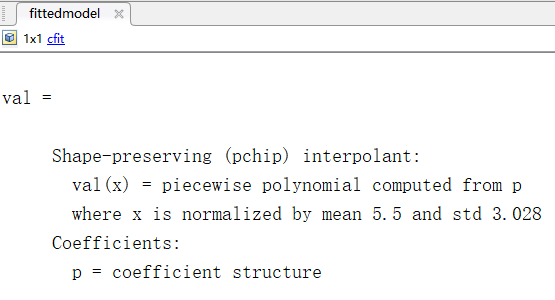
主要cfit格式的数据，就是我们保存下来的拟合关系，双击它可以查看详情。我这里保存的是拟合温度变化的拟合关系，是插值拟合，所以没有函数关系，只写明了是PCHIP插值。

那要怎么用这个拟合关系呢？它既然是一个关系，就需要自变量与因变量才能体现。如代码所演示：

% 设置自变量
xm=1:0.1:10;
% 将自变量套入刚刚保存的拟合关系里
ym=fittedmodel(xm);
plot(xm,ym,'+');

欸，这就是我们刚刚保存下来的拟合关系了，就是自变量与因变量的关系了，这种关系虽然没有准确的表达式，但也是一种映射关系，所以也能称之为函数吧。

其实，这个工具就是用可视化操作的方式来进行拟合工作，而写代码，用函数，写参数，也是可以完成拟合工作，而且可以设置的选项还会更多一些。时间所限，今天就先记录一下这个Curve Fitting工具的使用，等后面有空，再补充一下fittype函数的使用，也是用来拟合数据的。

今天的文章Matlab拟合——Curve Fitting工具分享到此就结束了，感谢您的阅读。