一、定义
顾名思义
向量的数乘运算,就是数量与向量相乘的运算
λ a → \mathop{a}\limits ^{\rightarrow} a→,λ∈R
二、λ a → \mathop{a}\limits ^{\rightarrow} a→的性质
1、长度
|λ|*| a → \mathop{a}\limits ^{\rightarrow} a→| = |λ a → \mathop{a}\limits ^{\rightarrow} a→|
2、方向
λ a → \mathop{a}\limits ^{\rightarrow} a→ 一定与 a → \mathop{a}\limits ^{\rightarrow} a→ 共线(平行)
λ > 0,λ a → \mathop{a}\limits ^{\rightarrow} a→的方向与 a → \mathop{a}\limits ^{\rightarrow} a→同向
λ = 0,λ a → \mathop{a}\limits ^{\rightarrow} a→ = 0 → \mathop{0}\limits ^{\rightarrow} 0→
λ < 0,λ a → \mathop{a}\limits ^{\rightarrow} a→的方向与 a → \mathop{a}\limits ^{\rightarrow} a→反向
3、数乘相关运算法则
符合交换律和分配率

注意
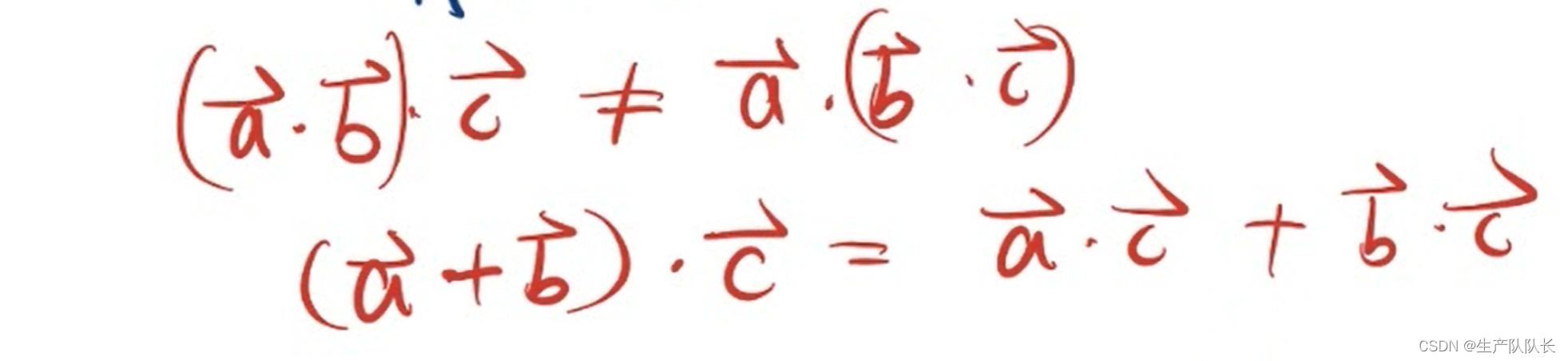
4、共线相关结论

三、练习
例题1

证明1:
省略号处是相似三角形的相关知识运用,通过三角形的相似,证明出MN∥BC

证明2:


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/81561.html