有限方法（冯康首次发现时称为基于变分原理的差分方法），是一种用于求解微分方程组或积分方程组数值解的数值技术。这一解法基于完全消除微分方程，即将微分方程转化为代数方程组（稳定情形）；或将偏微分方程（组）改写为常微分方程（组）的逼近，这样可以用标准的数值技术（例如欧拉法，龙格－库塔法等）求解。

有限方法的发展开始于五十年代中后期使用在机身框架和结构分析上，并于六十年代通过斯图加特大学的John Argyris和柏克莱加州大学的Ray W. Clough在土木工程中的应用工作中积累经验。1965年，冯康将其成果发表成论文。

FEM在理解起来并不困难，下面通过一个简单的例子，结合code，在说明这样一个问题。
1、首先考虑下面这样一个偏微分问题，物理建模过程略：

2、对于这个方程，任意找一个函数乘方程两边并进行积分，再利用分布积分公式，得到一个带积分的等式。进而，选取一组基函数，将$u$和$v$线性表出后代入，可将问题变为一个求解一个线性方程组问题。过程如下：

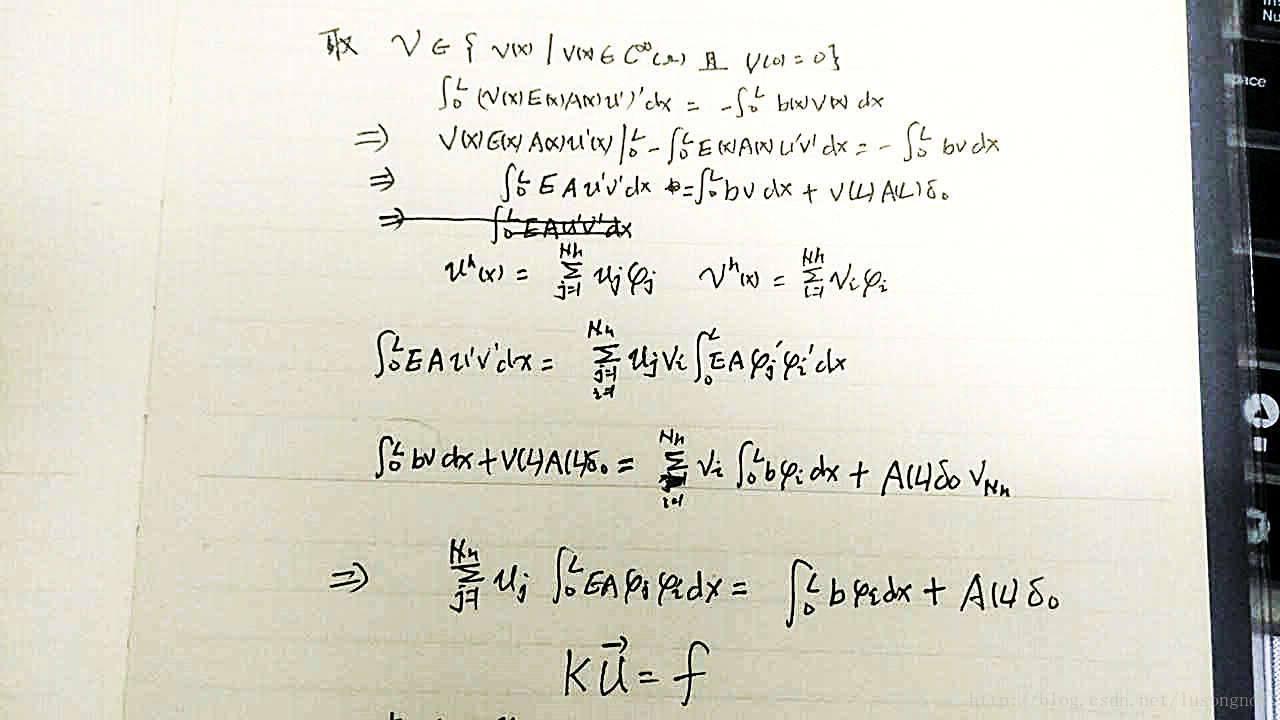
3、进一步，考虑到固有边界条件（$u(0)=u_0$），最后要对刚度矩阵和载荷向量进行校正，如下：

有限就是这么地简单，假如你认真看上面图片的话，应该能体会到。

下面给出这个问题的matlab代码：

主程序，调用了求解方程的函数：

%clear all; close all; L = 3; numel = 6; u_0 = 0; sigma_0 = 1; etype = 'linear'; fem1d(L,numel,u_0,sigma_0,etype); % Exact and numerical solution will be plotted. Exact solution for these % parameters can be found in exactsolution.m 

fem1d.m如下，给出了一个求解该问题的函数，相信注释比较清楚了，多余的东西就不说了。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Scientific Computing : Computational Methods for Nonlinear % Eigenvalue Problems, LSEC, Chinese Academy of Sciences, Beijing, China. %============================================================================ % % Finite Element Code for One-Dimensional Elasticity % -------------------------------------------------- % Author : Song Lu, LSEC % E-mail : lusongcool@163.com % %============================================================================ % % MODEL 1D Problem (Strong Form) % ============================== % One-dimensional Matlab finite element program to solve the following model % problem (one-dimetttttttttttttttt6nsional elasticity): % % (EAu')' + b = 0 in \Omega = (0,L) % where E(x) is the Young's modulus, A(x) is the cross-sectional area, and % b(x) is the body force per unit length. The functions for E, A and b are % set in m-files youngsmodulus.m, area.m and bodyforce.m, respectively. % % with boundary conditions % % u(0) = u_0 (essential boundary condition) % E(L)u'(L) = sigma_0 (natural boundary condition) % % FE Approximation % ================ % Galerkin method with linear finite elements % % ---------------------------------------- % USAGE: fem1d(L,numel,u_0,sigma_0,etype) % ---------------------------------------- % L : length of the bar % numel : number of elements (nodes are equi-spaced) % u_0 : essential BC at x = 0 % sigma_0 : traction at x = L % etype : element type (only option 'linear' is currently available) % Default : L = 3; numel = 6; u_0 = 0; sigma_0 = 1; etype = 'linear' % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function fem1d(L,numel,u_0,sigma_0,etype) clc; % clear command window close all; % close all figures % default values if nargin < 5, help(mfilename), %展示注释 L = 3; numel = 6; u_0 = 0; sigma_0 = 1; etype = 'linear'; fprintf('Executing with default settings \n \n'); end if L < 0, error('L must be positive'); end if numel < 1, error('Number of elements must be a natural number (1,2,...)'); end numnod = numel + 1; % no_of_nodes = no_of_elements + 1 (linear elements) % % check if element type (etype) is valid % switch lower(etype)%选择的类型，目前只有线性的。 case 'linear' nel = 2; disp('------------------------------------'); disp('FEM analysis with linear elements'); disp('------------------------------------'); case 'quadratic' nel = 3; disp('---------------------------------------'); disp('FEM analysis with quadratic elements'); disp('---------------------------------------'); error('Quadratic element type not coded yet'); otherwise fprintf('Element type = %s not defined\n',etype); error('Aborting!'); end % % Gauss quadrature (number of quadrature points) % nsp = 2; % Gauss-rule (nsp-point rule is used)%高斯点的个数 % nodal discretization coord = linspace(0,L,numnod)'; % `numnod' equally-spaced nodes between 0 and L %节点的坐标 % nodal connectivity array for elements in the FE mesh (numel x 2 matrix) connect = [1:(numnod-1); 2:numnod]'; %连接矩阵，表示哪些节点表示的基函数是连接的。 % essential boundaries ebcdof = [1]; % first node at x = 0 is constrained ebcval = [u_0]; % prescribed value %在第一个点的地方为u0 % initialize coefficient matrix [K] and external force vector {f} bigk = sparse(numnod,numnod); % stiffness matrix (initialized to zero) for [K] fext = sparse(numnod,1); % force vector (initialized to zero) for {f} % % element loop BEGIN % for e = 1:numel ke = elemstiff(e,nel,nsp,coord,connect); fe = elemforce(e,nel,nsp,coord,connect); sctr = connect(e,:); % % assemble element stiffness matrix % bigk(sctr,sctr) = bigk(sctr,sctr) + ke; % % assemble element force vector % fext(sctr) = fext(sctr) + fe; end % % element loop END % % % incorporate the traction boundary term in the force vector (refer to the % weak form) % xend = coord(numnod); fext(numnod) = fext(numnod) + area(xend)*sigma_0; % % essential boundary conditions % % modify rows in K and f to incorporate the essential boundary condition %根据本质边界条件进行校正 for i = 1:length(ebcdof) n = ebcdof(i); for j = 1:numnod if (isempty(find(ebcdof == j))) % dof j is not found in ebcdof vector fext(j) = fext(j) - bigk(j,n)*ebcval(i); end end bigk(n,:) = 0.0; bigk(:,n) = 0.0; bigk(n,n) = 1.0; fext(n) = ebcval(i); end % % solve for nodal unknowns % u_coeff = inv(bigk)*fext; % % determine derivative of approximation in each element : for linear elements % the strain (u') is a constant in each element and is given by the difference % of the nodal displacements divided by the length of the element % %求数值解的导数，因为用直线逼近，每一段都是一个常数 for e = 1:numel he = coord(connect(e,2)) - coord(connect(e,1)); uprime(2*e-1) = (u_coeff(connect(e,2)) - u_coeff(connect(e,1)))/he; uprime(2*e) = uprime(2*e-1); xp(2*e-1) = coord(connect(e,1)); xp(2*e) = coord(connect(e,2)); end % % exact solution : see exactsolution.m % % % number of sampling point to compute the exact solution for plotting purposes nsamp = 101; % xsamp = linspace(0,L,nsamp); for j = 1:length(xsamp) [uex,uexder] = exactsolution(xsamp(j)); uexact(j) = uex; uprimeexact(j) = uexder; end % % plot results % if (numel > 20) plot(coord,u_coeff,'-',xsamp,uexact,'--'); else plot(coord,u_coeff,'-',xsamp,uexact,'--',... coord,zeros(numnod,1),'mo','MarkerEdgeColor','k',... 'MarkerFaceColor',[0.5 1 0.6],'MarkerSize',10); end h = legend('FE solution','Exact solution','location','best'); set(h,'fontsize',14); title('Comparison of FE and Exact Solutions'); xt = get(gca,'XTickLabel'); set(gca,'XTickLabel',xt,'fontsize',12); yt = get(gca,'XTickLabel'); set(gca,'XTickLabel',yt,'fontsize',12); xlabel('$x$','Interpreter','latex','fontsize',16) ylabel('$u^h , u$','Interpreter','latex','fontsize',16); figure; if (numel > 20) plot(xp,uprime,'-',xsamp,uprimeexact,'--'); else plot(xp,uprime,'-',xsamp,uprimeexact,'--',... coord,zeros(numnod,1),'mo','MarkerEdgeColor','k',... 'MarkerFaceColor',[0.5 1 0.6],'MarkerSize',10); end h = legend('FE derivative','Exact derivative','location','best'); set(h,'fontsize',14); title('Comparison of FE and Exact Derivative Solutions'); title('Comparison of FE and Exact Derivative Solutions'); xt = get(gca,'XTickLabel'); set(gca,'XTickLabel',xt,'fontsize',12); yt = get(gca,'XTickLabel'); set(gca,'XTickLabel',yt,'fontsize',12); xlabel('$x$','Interpreter','latex','fontsize',16) ylabel('$u_{,x}^h , u_{,_x}$','Interpreter','latex','fontsize',16); return end 

一些子函数：

elemstiff.m function [ke] = elemstiff(e,nel,nsp,coord,connect) % % Purpose % ======= % Element stiffness matrix for one-dimensional fem % % Input % ----- % e : element number % nel : nodes per element % nsp : no of Gauss points % coord : coordinates of the nodes % connect : nodal connectivity  %  % Output % ------ % Element stiffness matrix ke (nel x nel matrix) % % % initialize element stiffness matrix to zero % ke = zeros(nel,nel); nodes = connect(e,:); xe = coord(nodes); % x-coordinate of nodes Le = xe(nel) - xe(1);%connect只有两列，这里为什么要用nel，考虑到隔一个也有交叉的基函数 detj = Le/2; % % loop over Gauss points in xi-direction % xi = gauss_points(nsp);%-1到1上的高斯点 weight = gauss_weights(nsp);%高斯权重 for i = 1:nsp % % shape function and derivative of N (B-matrix) % N = [ 0.5*(1 - xi(i)) 0.5*(1 + xi(i))];%基函数在高斯点上的值 B = 1/Le*[-1 1]; % detj = L/2 求基函数的在高斯点的导数，即斜率 xg = N*xe; %表示xe区间上高斯点的坐标 % % assemble element stiffness matrix ke  % Ax = area(xg);%界面面积一般和位置也有关 Ex = youngsmodulus(xg);%杨氏模量和位置有关 ke = ke + weight(i)*Ex*Ax*B'*B*detj; end return end elemforce.m function [fe] = elemforce(e,nel,nsp,coord,connect) % % Purpose % ======= % Element force vector for one-dimensional fem % % Input % ----- % e : element number % nel : nodes per element % nsp : no of Gauss points % coord : coordinates of the nodes % connect : nodal connectivity  %  % Output % ------ % Element force vector fe (nel x 1 vector) % % % initialize element force vector to zero % fe = zeros(nel,1); nodes = connect(e,:); xe = coord(nodes); % x-coordinate of nodes Le = xe(nel) - xe(1); detj = Le/2; % % loop over Gauss points in xi-direction % xi = gauss_points(nsp); weight = gauss_weights(nsp); for i = 1:nsp % % shape function N % N = [ 0.5*(1 - xi(i)) 0.5*(1 + xi(i)) ]; xg = N*xe; % % assemble element force vector ke % bx = bodyforce(xg); fe = fe + weight(i)*bx*N'*detj; end return end guass_points.m function x = guass_points(n); % % function x = gauss_points(n) % % For 1 <= n <= 20, returns the abscissas x of an n point % Gauss-Legendre quadrature rule over the interval [-1,1]. % x = ones(1,n); if ( n == 1 ) x(1) = 0.0; elseif ( n == 2 ) x(1) = - 0.; x(2) = 0.; elseif ( n == 3 ) x(1) = - 0.; x(2) = 0.000000000000000; x(3) = 0.; elseif ( n == 4 ) x(1) = - 0.; x(2) = - 0.; x(3) = 0.; x(4) = 0.; elseif ( n == 5 ) x(1) = - 0.; x(2) = - 0.; x(3) = 0.0; x(4) = 0.; x(5) = 0.; elseif ( n == 6 ) x(1) = - 0.0; x(2) = - 0.; x(3) = - 0.0; x(4) = 0.0; x(5) = 0.; x(6) = 0.0; elseif ( n == 7 ) x(1) = - 0.; x(2) = - 0.; x(3) = - 0.0; x(4) = 0.0; x(5) = 0.0; x(6) = 0.; x(7) = 0.; elseif ( n == 8 ) x(1) = - 0.; x(2) = - 0.; x(3) = - 0.; x(4) = - 0.; x(5) = 0.; x(6) = 0.; x(7) = 0.; x(8) = 0.; elseif ( n == 9 ) x(1) = - 0.; x(2) = - 0.; x(3) = - 0.0; x(4) = - 0.; x(5) = 0.0; x(6) = 0.; x(7) = 0.0; x(8) = 0.; x(9) = 0.; elseif ( n == 10 ) x(1) = - 0.; x(2) = - 0.; x(3) = - 0.; x(4) = - 0.; x(5) = - 0.; x(6) = 0.; x(7) = 0.; x(8) = 0.; x(9) = 0.; x(10) = 0.; elseif (n == 11) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.; x(6)= 0; x(7)= 0.; x(8)= 0.; x(9)= 0.; x(10)= 0.; x(11)= 0.; elseif (n == 12) x(1)=-0.; x(2)=-0.0; x(3)=-0.; x(4)=-0.0; x(5)=-0.; x(6)=-0.; x(7)= 0.; x(8)= 0.; x(9)= 0.0; x(10)= 0.; x(11)= 0.0; x(12)= 0.; elseif (n == 13) x(1)=-0.; x(2)=-0.; x(3)=-0.0; x(4)=-0.0; x(5)=-0.; x(6)=-0.; x(7)= 0; x(8)= 0.; x(9)= 0.; x(10)= 0.0; x(11)= 0.0; x(12)= 0.; x(13)= 0.; elseif (n == 14) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.; x(6)=-0.; x(7)=-0.; x(8)= 0.; x(9)= 0.; x(10)= 0.; x(11)= 0.; x(12)= 0.; x(13)= 0.; x(14)= 0.; elseif (n == 15) x(1)=-0.0; x(2)=-0.0; x(3)=-0.0; x(4)=-0.0; x(5)=-0.; x(6)=-0.0; x(7)=-0.; x(8)= 0; x(9)= 0.; x(10)= 0.0; x(11)= 0.; x(12)= 0.0; x(13)= 0.0; x(14)= 0.0; x(15)= 0.0; elseif (n == 16) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.0; x(5)=-0.; x(6)=-0.; x(7)=-0.; x(8)=-0.0; x(9)= 0.0; x(10)= 0.; x(11)= 0.; x(12)= 0.; x(13)= 0.0; x(14)= 0.; x(15)= 0.; x(16)= 0.; elseif (n == 17) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.0; x(6)=-0.; x(7)=-0.; x(8)=-0.; x(9)= 0; x(10)= 0.; x(11)= 0.; x(12)= 0.; x(13)= 0.0; x(14)= 0.; x(15)= 0.; x(16)= 0.; x(17)= 0.; elseif (n == 18) x(1)=-0.0; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.0; x(6)=-0.; x(7)=-0.; x(8)=-0.; x(9)=-0.0; x(10)= 0.0; x(11)= 0.; x(12)= 0.; x(13)= 0.; x(14)= 0.0; x(15)= 0.; x(16)= 0.; x(17)= 0.; x(18)= 0.0; elseif (n == 19) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.; x(6)=-0.; x(7)=-0.; x(8)=-0.; x(9)=-0.0; x(10)= 0; x(11)= 0.0; x(12)= 0.; x(13)= 0.; x(14)= 0.; x(15)= 0.; x(16)= 0.; x(17)= 0.; x(18)= 0.; x(19)= 0.; elseif (n == 20) x(1)=-0.; x(2)=-0.; x(3)=-0.; x(4)=-0.; x(5)=-0.0; x(6)=-0.; x(7)=-0.0; x(8)=-0.; x(9)=-0.; x(10)=-0.00; x(11)= 0.00; x(12)= 0.; x(13)= 0.; x(14)= 0.0; x(15)= 0.; x(16)= 0.0; x(17)= 0.; x(18)= 0.; x(19)= 0.; x(20)= 0.; else error('GAUSS_WEIGHTS - Fatal error! Illegal value of n.') end return end gauss_weights.m function w = gauss_weights(n); % % function w = gauss_weights(n); % % For 1 <= n <= 20, returns the weights W of an % n point Gauss-Legendre quadrature rule over the interval [-1,1]. % w = ones(1,n); if ( n == 1 ) w(1) = 2.0; elseif ( n == 2 ) w(1) = 1.0; w(2) = w(1); elseif ( n == 3 ) w(1) = 0.; w(2) = 0.; w(3) = 0.; elseif ( n == 4 ) w(1) = 0.; w(2) = 0.; w(3) = 0.; w(4) = 0.; elseif ( n == 5 ) w(1) = 0.; w(2) = 0.; w(3) = 0.; w(4) = 0.; w(5) = 0.; elseif ( n == 6 ) w(1) = 0.; w(2) = 0.; w(3) = 0.; w(4) = 0.; w(5) = 0.; w(6) = 0.; elseif ( n == 7 ) w(1) = 0.; w(2) = 0.; w(3) = 0.; w(4) = 0.0; w(5) = 0.; w(6) = 0.; w(7) = 0.; elseif ( n == 8 ) w(1) = 0.0; w(2) = 0.; w(3) = 0.; w(4) = 0.; w(5) = 0.; w(6) = 0.; w(7) = 0.; w(8) = 0.0; elseif ( n == 9 ) w(1) = 0.0; w(2) = 0.; w(3) = 0.; w(4) = 0.00006584; w(5) = 0.; w(6) = 0.00006584; w(7) = 0.; w(8) = 0.; w(9) = 0.0; elseif ( n == 10 ) w(1) = 0.0; w(2) = 0.0; w(3) = 0.; w(4) = 0.; w(5) = 0.; w(6) = 0.; w(7) = 0.; w(8) = 0.; w(9) = 0.0; w(10) = 0.0; elseif ( n == 11 ) w(1)= 0.0; w(2)= 0.; w(3)= 0.; w(4)= 0.; w(5)= 0.0; w(6)= 0.; w(7)= 0.0; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.0; elseif ( n == 12 ) w(1)= 0.0; w(2)= 0.; w(3)= 0.; w(4)= 0.; w(5)= 0.; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.; w(12)= 0.0; elseif ( n == 13 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.0; w(4)= 0.; w(5)= 0.; w(6)= 0.; w(7)= 0.0; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.0; w(12)= 0.0; w(13)= 0.0; elseif ( n == 14 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.; w(4)= 0.0; w(5)= 0.; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.0; w(12)= 0.; w(13)= 0.0; w(14)= 0.0; elseif ( n == 15 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.; w(4)= 0.0; w(5)= 0.00; w(6)= 0.00; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.00; w(11)= 0.00; w(12)= 0.0; w(13)= 0.; w(14)= 0.0; w(15)= 0.0; elseif ( n == 16 ) w(1)= 0.00; w(2)= 0.0; w(3)= 0.0; w(4)= 0.; w(5)= 0.0; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.; w(12)= 0.0; w(13)= 0.; w(14)= 0.0; w(15)= 0.0; w(16)= 0.00; elseif ( n == 17 ) w(1)= 0.000; w(2)= 0.00; w(3)= 0.0; w(4)= 0.; w(5)= 0.; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.; w(12)= 0.; w(13)= 0.; w(14)= 0.; w(15)= 0.0; w(16)= 0.00; w(17)= 0.000; elseif ( n == 18 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.0; w(4)= 0.; w(5)= 0.; w(6)= 0.0; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.; w(12)= 0.; w(13)= 0.0; w(14)= 0.; w(15)= 0.; w(16)= 0.0; w(17)= 0.0; w(18)= 0.0; elseif ( n == 19 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.0; w(4)= 0.0; w(5)= 0.; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.; w(11)= 0.; w(12)= 0.; w(13)= 0.; w(14)= 0.; w(15)= 0.; w(16)= 0.0; w(17)= 0.0; w(18)= 0.0; w(19)= 0.0; elseif ( n == 20 ) w(1)= 0.0; w(2)= 0.0; w(3)= 0.0; w(4)= 0.0; w(5)= 0.; w(6)= 0.; w(7)= 0.; w(8)= 0.; w(9)= 0.; w(10)= 0.0; w(11)= 0.0; w(12)= 0.; w(13)= 0.; w(14)= 0.; w(15)= 0.; w(16)= 0.; w(17)= 0.0; w(18)= 0.0; w(19)= 0.0; w(20)= 0.0; else error('GAUSS_WEIGHTS - Fatal error! Illegal value of n.') end return end area.m function Ax = area(xg) % % Cross-sectional area % Ax = 1; return end bodyforce.m function bx = bodyforce(xg) % % body force % bx = 1; return end youngsmodulus.m function Ex = youngsmodulus(xg) % % Young's modulus % Ex = 1; return end exactsolution.m function [uexact,uexactder] = exactsolution(xg) % % exact solution for L = 3, b = 1, E = 1, A = 1, u_0 = 0, sigma_0 = 1 % uexact = 4.*xg - xg^2/2.; uexactder = 4. - xg; return end 

需要注意的是，杨氏模量等量需要根据实际物理问题给出，这里设置为常数。另外，高斯点和高斯权重是用于求积分的，程序中直接给出了数据，实际的求法可以做正交多项式，取次数最高项求零点即可，详见我的另外一篇博客。
高斯积分方法

在解偏微分方程的过程中，主要的难点 是如何构造一个方程来逼近原本研究的方程，并且该过程还需要保持数值稳定性。目前有许多处理的方法，他们各有利弊。当区域改变时（就像一个边界可变的固体），当需要的精确度在整个区域上变化，或者当解缺少光滑性时，有限方法是在复杂区域（像汽车、船体结构、输油管道）上解偏微分方程的一个很好的选择。例如，在正面碰撞仿真时，有可能在”重要”区域（例如汽车的前部）增加预先设定的精确度并在车辆的末尾减少精度（如此可以减少仿真所需消耗）;另一个例子是模拟地球的气候模式，预先设定陆地部分的精确度高于广阔海洋部分的精确度是非常重要的。

考虑到方便，变分推导过程就手写了；数学上的表述往往越严格越难理解，为了通俗易懂，有些地方故意说得不是那么严格，甚至懂的人会有看法；为了好理解，尽量避开了符号和专业术语。