编译原理第五章——自下而上分析——算符优先分析
目录
- 一、复习:语法分析的两种方式
- 二、自下而上分析概述
- 1.🐯核心思想:移进-规约
- 2.⛺️规范规约
- 3.🦁规范规约的两个问题
- 三、算符优先分析
- 1.🐸概念辨析-算符文法、算符优先文法
- 2.🐙概念辨析-算符优先分析法、直观算符优先分析法
- 3.🐬概念辨析-算符文法、算符优先文法
- 4.🐳 利用优先关系表用直观算符优先分析法分析算数表达式不考可以跳过
- 5.🐂构造FIRSTVT§和LASTVT§两个集合必考!!
- 6.🐝利用FIRSTVT§和LASTVT§两个集合构造优先关系表必考!!
- 7.🐇素短语
- 8.🐏优先函数感觉不会考,至少掌握下概念吧
前面部分的链接: 编译原理第五章——自下而上分析——概述
三、直观算符优先分析法
1.🐸概念辨析-算符文法、算符优先文法
- 算符文法
- 设有一个文法G,若G中有形如U->Vw的产生式,即它的任意产生式的右部都不含两个相继的非终结符,则称G为算数文法,或称为OG文法。
- 重点:不允许有两个连续的非终结符。
- 算符优先文法

- 符号解释
- 形似><+的符号,没有传递性,也没有反对称性!!!
- 他们只是描述两个终结符的优先关系。
- 读作:a的优先级低于(高于)(等于)b。
2.🐙概念辨析-算符优先分析法、直观算符优先分析法
- 直观算符优先分析法:
- 基于直觉的、手工进行分析的方法,通常用于简单的文法或教学目的。
- 算符优先分析法:
- 是一种自动化的语法分析技术,通常用于编译器设计和实现中。
- 二者本质是一个东西,都是效仿四则运算的计算过程而构造的一种语法分析方法。算符优先分析法的关键是比较两个相继出现的终结符的优先级而决定应采取的动作。
- 优点:简单有效,适合表达式的分析。
- 缺点:只适合于算符优先文法,是一个不大的文法类。
- 算符优先分析过程是自下而上的归约过程,但未必是严格的最左归约。也就是说,算符优先分析法不是一种规范归约法。所谓【算符优先分析法】就是定义算符之间的某种优先关系,借助于这种关系寻找“可归约串”进行归约的一种方法。
- 换言之,我们没有解决自下而上分析的两个问题,只是挑了一种容易分析的文法。
3.🐬 概念辨析-算符文法、算符优先文法
- 概念层面:算符文法是一种文法的类型,而算符优先文法是一种分析方法。算符文法定义了文法的结构,以便可以使用算符优先分析法进行解析。
- 应用范围:算符文法专门针对文法的结构,确保文法适合进行算符优先分析。算符优先文法则更广泛地指代一种分析技术,它可以用来解析满足特定条件的文法。
- 目的:算符文法的目的是为了确保文法的结构允许使用算符优先分析法,而算符优先文法的目的是为了提供一个有效的解析策略,以便能够处理具有优先级规则的表达式。
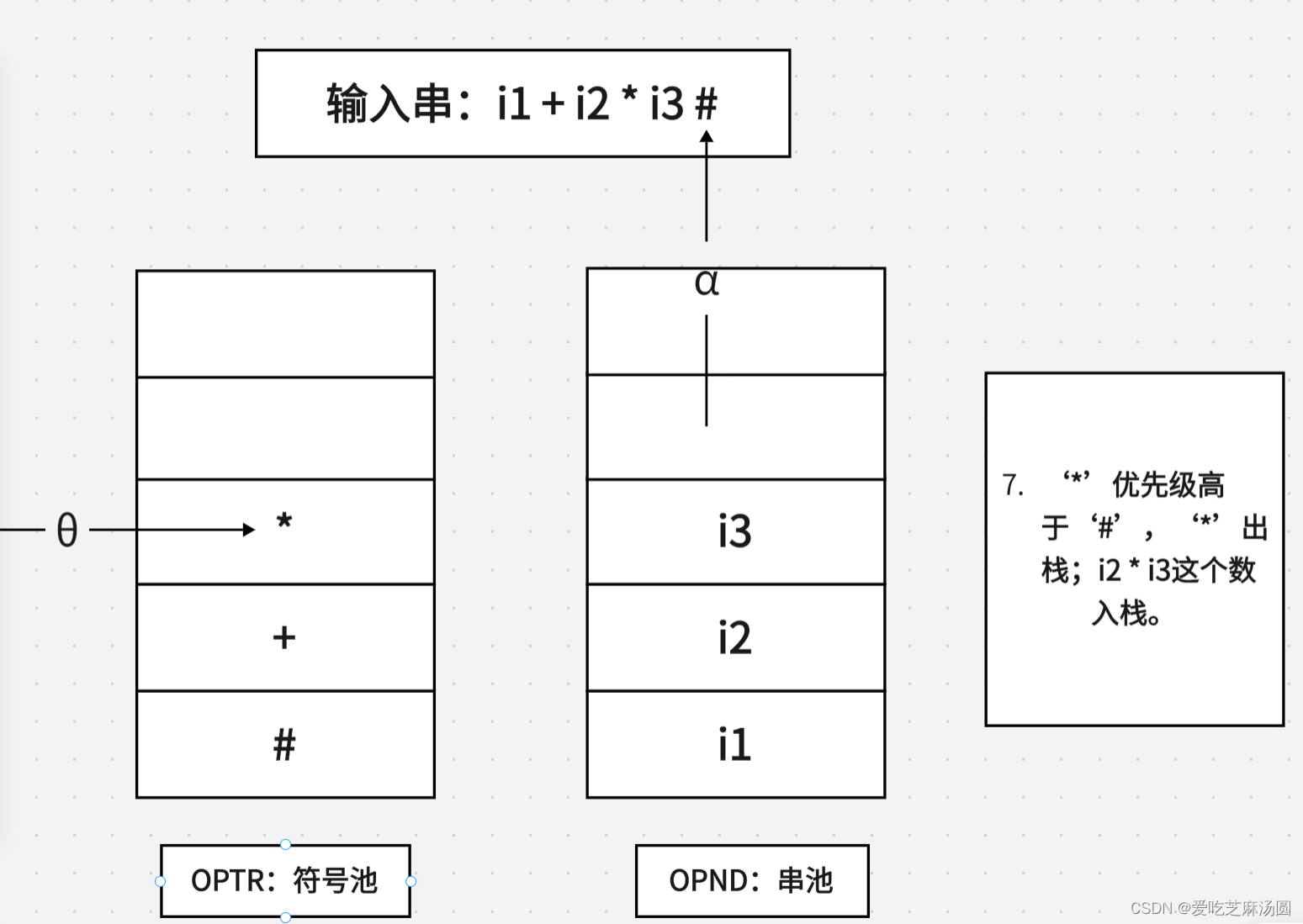
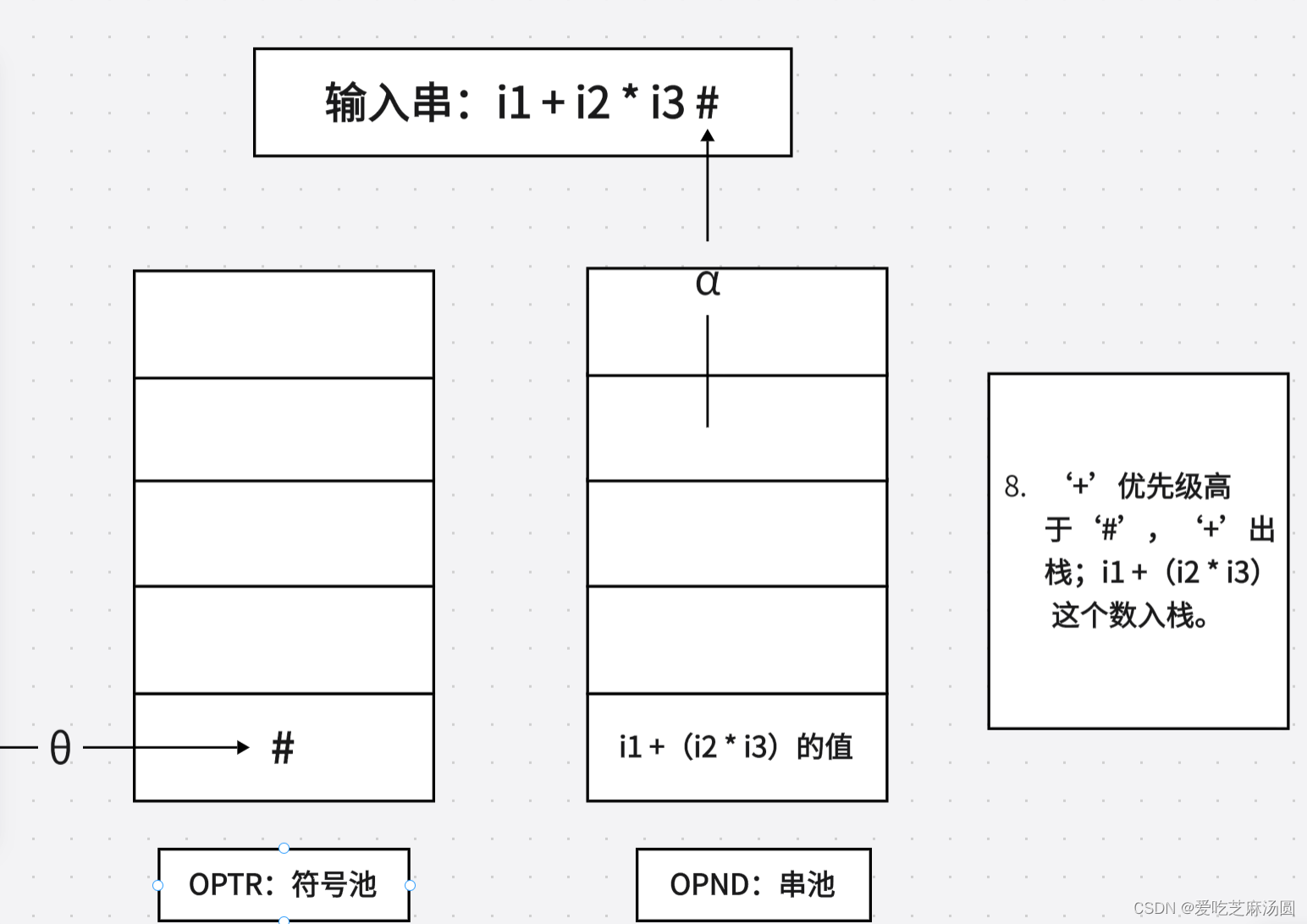
4.🐳 利用优先关系表用直观算符优先分析法分析算数表达式(这玩意不考时间紧可以跳过)
记号使用说明
- #:语句括号(栈底和输入串w后)
- θ:运算符栈的栈顶符
- a:刚读入终结符号
- OPTR:运算符栈
- OPND:操作数栈
分析算法步骤
- 下面的><=都是优先符号
-
- 下一个输入终结符号读至a中。
-
- 若a为i,则a入栈OPND,然后转第一步。
-
- 若0 > a,则调用关于日的处理程序(语义程序),处理子表达式:E(1)0E(2)(其中,E(1)、E(2)分别为操作数OPND栈的次栈顶和栈顶);将上述子表达式的结果再填入OPND栈;然后重新进入第3步。
-
- 若θ = a,则
- 若0 = '('并且a = ‘)’,则逐出OPTR栈顶的‘(’并且放弃a中的‘)’,然后转第1步;
- 若0=a=‘#',则分析成功结束。
- 若θ = a,则
-
- 若θ< a,则a入栈OPTR,然后转第1步。
-
- 若0与a不存在优先关系,则判输入串错误,调出错处理。
- 是不是看不懂,巧了我也是,看例题吧
例题
对于文法G:E->E+E|E*E|E↑E|(E)|i
其终结符的优先关系见下表。 但其实不用看,这里就是算数运算的符号优先级
PS:下面的><=都是优先符号
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | > | > |
| * | > | > | < | < | < | > | > |
| ↑ | > | > | < | < | < | > | > |
| i | > | > | > | > | > | ||
| ( | < | < | < | < | < | = | |
| ) | > | > | > | > | > | ||
| # | < | < | < | < | < | = |





5.🐂构造FIRSTVT§和LASTVT§两个集合
牢记:FIRSTVT和LASTVT的意义:首/尾终结符集
FIRSTVT构造方法:
- 若有产生式 P -> a …或者P -> Q a …,那么a属于FIRSTVT§。
- 若a属于FIRSTVT(Q),且有产生式P -> Q…,那么a属于FIRSTVT§。
例 文法
E -> T | E + T
T -> F | T * F
F -> P | P ↑ F
P -> i | ( E )
构造FIRSTVT和LASTVT。
解
- 首先利用FIRSTVT构造方法的1,从上往下,得到:
- FIRSTVT(E)={+}
- FIRSTVT(T)={*}
- FIRSTVT(F)={↑}
- FIRSTVT§={i , (}
- 然后利用FIRSTVT构造方法的2,从下往上,得到:
- FIRSTVT(E)={+ , * , ↑ , i , (}
- FIRSTVT(T)={* , ↑ , i , (}
- FIRSTVT(F)={↑ , i , (}
- FIRSTVT§={i , (}
- FIRSTVT与LASTVT构造方式完全对称,直接给出:
- LASTVT(E)={+ , * , ↑ , i , )}
- LASTVT(T)={* , ↑ , i , )}
- LASTVT(F)={↑ , i , )}
- LASTVT§={i , )}
6.🐝利用FIRSTVT§和LASTVT§两个集合构造优先关系表
优先关系表构造方法:
#和#一定相等,直接填入

例 文法
E -> T | E + T
T -> F | T * F
F -> P | P ↑ F
P -> i | ( E )
构造其优先关系表。
解
- 1.先找优先级相等的关系:#和#一定相等,直接填入,P -> ( E ),则( = )。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | |||||||
| * | |||||||
| ↑ | |||||||
| i | |||||||
| ( | = | ||||||
| ) | |||||||
| # | = |
- 2.然后从上往下分析,E -> E + T,其中E +符合第四条,那么LASTVT(E)的每个素优先级>+。
- 这个怎么理解呢?首先我们知道,优先级表的第一列是前面那个非终结符,第一行是后面那个终结符;其次我们可以这样理解,非终结符优先规约,那么E的终结符的优先级更高;那到底选是E的LASTVT还是FIRSTVT呢,因为+在后面,肯定选LASTVT。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | ||||||
| * | > | ||||||
| ↑ | > | ||||||
| i | > | ||||||
| ( | = | ||||||
| ) | > | ||||||
| # | = |
- 同理继续分析,这里我多写几个帮助理解,E -> E + T,其中+ T符合第三条,那么+的优先级小于FIRSTVT(T)。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | ||
| * | > | ||||||
| ↑ | > | ||||||
| i | > | ||||||
| ( | = | ||||||
| ) | > | ||||||
| # | = |
- 同理继续分析,T ->T F,其中T符合第四条,那么LASTVT(T)的每个素优先级> *。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | ||
| * | > | > | |||||
| ↑ | > | > | |||||
| i | > | > | |||||
| ( | = | ||||||
| ) | > | > | |||||
| # | = |
- 同理继续分析,T ->T F,其中 F符合第三条,那么*的优先级小于FIRSTVT(F)的每个素。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | ||
| * | > | > | < | < | < | ||
| ↑ | > | > | |||||
| i | > | > | |||||
| ( | = | ||||||
| ) | > | > | |||||
| # | = |
- 同理继续分析,给出差最后一步的答案:
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | > | |
| * | > | > | < | < | < | > | |
| ↑ | > | > | < | < | < | > | |
| i | > | > | > | > | |||
| ( | < | < | < | < | < | = | |
| ) | > | > | > | > | |||
| # | = |
- 好滴,千万不要忘记最后一步:S -> # E #,满足# E,那么#的优先级低于FIRSTVT(E)的每一个素,满足E #,那么LASTVT(E)的每一个素优先级都大于#。
| + | * | ↑ | i | ( | ) | # | |
|---|---|---|---|---|---|---|---|
| + | > | < | < | < | < | > | > |
| * | > | > | < | < | < | > | > |
| ↑ | > | > | < | < | < | > | > |
| i | > | > | > | > | > | ||
| ( | < | < | < | < | < | = | |
| ) | > | > | > | > | > | ||
| # | < | < | < | < | < | = |
至此构造完成!
7.🐇素短语
素短语概念
- 所谓素短语是指这样一个短语,它至少含有一个终结符,并且除自身之外不再含任何更小的素短语。
- 句型最左边的那个素短语叫最左素短语。
- 注意:素短语和直接短语很类似,但没有啥关系。
- 注意:素短语是算符优先文法中的概念,因此可以说素短语是算符优先文法特有的。
- 判断方式1:根据语法树判断:
- 素短语递归定义,满足三个条件:
① 素短语是短语。
② 素短语中必须包含至少一个终结符。
③ 素短语中不能包含其它素短语。 - 判断方式2:根据优先关系判断:被优先关系符号所包裹(看例题吧讲不清定义又太复杂)
例 文法
E -> T | E + T
T -> F | T F
F -> P | P ↑ F
P -> i | ( E )
对于句型:i_1(i_2 + i_3)
解1
语法树如下:

- 短语:i_1,i_2,i_3,i_2+i_3,(i_2+i_3),i_1*(i_2+i_3)
- 素短语:i_1,i_2,i_3
- 最左素短语:i_1
- 这玩意复杂度堪称炸裂级别的,所以十分不建议使用方法一去解。
解2
直接扣图,看图~

哈哈真简单(所以我为什么要费那么大劲去构造语法树😢😢😢)
8.🐏优先函数
定义
- 我们把每个终结符θ与两个自然数f(θ)和g(θ)相对应,使得:
- 若θ_1 < θ_2,则f(θ_1) < g(θ_2)
- 若θ_1 = θ_2,则f(θ_1) = g(θ_2)
- 若θ_1 > θ_2,则f(θ_1) > g(θ_2)
- 函数f称为入栈优先函数,g称为比较优先函数。
使用优先函数的优缺点
- 优:便于比较运算;节省存储空间。
- 缺:对不存在优先关系的两个终结符,由于与自然数相对应,变成可比较。
优先函数的性质
- 正确性:优先函数掩盖了矩阵中出错素对,若f(id) < g(id),暗示id < id,但id之间无优先关系,因此失去发现错误能力,但并未严重到妨碍在可解地方使用优先函数。
- 存在性:并非总能把表映射到优先函数,例如下面这个:
| a | b | |
|---|---|---|
| a | = | > |
| b | = | = |
- 唯一性:如果存在一个优先函数,则有无数多对,原因在于:加任一常数,不等式仍成立。
构造优先函数的方式
- 对每个a(包括#)属于V_T,对应两个符号f_a,g_a.
- 把符号尽可能划分为许多组:
- 若a = b,则f_a和g_b就在一组;
- 若a = b,c = b,则f_a和f_c。同组;
- 建立一个有向图,其结点是上一步中找出的组。
- 对于任何a和b,若 a > b,画 f_a -> g_b弧,意味着f(a) > g(b);
- 若a < b,画 g_b -> f_a弧,意味着f(a) < g(b)。
- 如果上一步结果构成环,则f,g不存在;
- 否则 f(a) = 从f组开始的路径和;
- g (b)= 从sb组开始的路径和。
具体例子不再给出,应该不考,不是重点。
今天的文章 编译原理第五章——自下而上分析——算符优先分析(超全)分享到此就结束了,感谢您的阅读。


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/83502.html