前言

赋值法是高中数学中比较常用的一种方法，使用“赋值法”的数学素材和知识点，散落在高中数学的几乎各个章节中，现对其进行整理，以便于学习。比如学习函数时可以赋值法给出单调性，奇偶性，周期性等，求函数的值，

一、赋值法的理论依据

比如给定\(R\)上的函数\(f(x)\)，满足条件\(f(x+y)=f(x)+f(y)\)，则我们就可以令\(x=1，y=1\)，得到\(f(2)=f(1)+f(1)=2f(1)\)；当然也可以令\(x=1，y=0\)，得到\(f(1)=f(1)+f(0)\)，从而得到\(f(0)=0\)，实际上由于是\(R\)上的函数\(f(x)\)，那么我们给\(x、y\)任意赋值都是合理的，这样就能得到无穷个等式，但是我们解题不需要这么多，只需要有针对性的一两个，所以我们其实是有目的的赋值的，那么到底该怎么赋值呢，这要结合具体题目来分析，需要一定的数学素养。

二、使用赋值法的数学素材

1、判断抽象函数性质

例1-单调性

如定义在\(R\)上的函数\(f(x)\)满足\(f(x+y)=f(x)+f(y)\)，且\(x >0\)时，\(f(x)<0\)，判定函数单调性。

分析：令\(x_1> x_2\)，则\(x_1-x_2>0\)，故\(f(x_1-x_2)<0\)，

则有$ f(x_1) = f(x_1-x_2+x_2) = f(x_1-x_2)+f (x_2) < f( x_2) $，

故函数\(f(x)\)在\(R\)上单调递减。

已知函数\(f(x)\)满足\(f(1)=\cfrac{1}{2}\)，且\(f(x+y)+f(x-y)=2f(x)f(y)\)，判断函数的奇偶性；

分析：令\(x=y=0\)，则有\(2f(0)=2f^2(0)\)，得到\(f(0)=0或f(0)=1\)；

再令\(x=1，y=0\)，则有\(2f(1)=2f(1)f(0)\)，得到\(f(0)=1\)；

又题目已知\(f(1)=\cfrac{1}{2}\)，

若令\(x=0\)，则得到\(f(y)+f(-y)=2f(0)f(y)=2f(y)\)，

所以\(f(-y)=f(y)\)，可知函数是偶函数。

比如已知定义在\(R\)上的函数满足\(f(x+6)=f(x)+f(3)\)，且函数\(f(x)\)是偶函数，试判断函数的周期性。

分析：由于\(f(x+6)=f(x)+f(3)\)，

令\(x=-3\)，则\(f(-3+6)=f(-3)+f(3)\)，

即\(f(-3)=0\)，又由于\(f(-x)=f(x)\)，

则有\(f(-3)=f(3)=0\)，那么原式变为

\(f(x+6)=f(x)\)，即\(T=6\)；

引申：已知\(f(x+6)=f(x)+nf(3)(n\in N^*)\)，再加上\(f(x)\)是偶函数，\(\Longrightarrow T=6\)

提示：用赋值法，令\(x=-3\)，\(f(-3+6)=f(-3)+nf(3)\)推出\(f(3)=0\)，

从而\(f(x+6)=f(x)，\)故\(T=6\)。

例4-对称性

已知函数\(f(x)=\cfrac{2^x}{1+a\cdot 2^x}(a\in R)\)的图像关于点\((0，\cfrac{1}{2})\)对称，则\(a=\)_______。

分析：由题目可知，\(f(x)+f(-x)=1\)，

法1，定义法，对定义域内的任意\(x\)，必须恒有\(f(x)+f(-x)=1\)，由\((a-1)[2^{2x}+(a-1)2^x+1]=0\)恒成立，故必须\(a-1=0\)，从而得到\(a=1\)；

法2，赋值法，比如\(f(0)+f(-0)=1\)，变形为\(\cfrac{2}{1+a}=1\)，得到\(a=1\)，当然这个方法要注意定义域。

2、抽象函数求值

例5【2019届高三理科函数的奇偶性周期性课时作业第13题】

设定义在\(R\)上的函数\(f(x)\)同时满足以下条件：

①\(f(x)+f(-x)=0\)；

②\(f(x)=f(x+2)\)；

③当\(0\leq x<1\)时，\(f(x)=2^x-1\)，

则\(f(\cfrac{1}{2})+f(1)+f(\cfrac{3}{2})+f(2)+f(\cfrac{5}{2})\)的值是_________。

分析：由①知，函数为奇函数，在利用③先做出\([0，1)\)上的图像，

再利用奇函数，做出\((-1，0]\)上的图像，一个周期基本完成，就差端点值\(f(-1)\)和\(f(1)\)的值未确定；

难点是求\(f(1)\)的值，可以通过以下几个思路求解，

法1：图像法，假设\(f(1)=\cfrac{1}{2}\)，则\(f(-1)=-\cfrac{1}{2}\)，奇偶性是说的通的，

但是周期性不满足，因为向右平移一个周期后，素\(1\)对应\(\cfrac{1}{2}\)，还对应\(-\cfrac{1}{2}\)，

出现了一对多，不是函数了，故只能有\(f(1)=0\)，即也有\(f(-1)=0\)，

这样在一个周期上奇偶性和周期性都是满足的。

法2：题中没有明确告诉，但是由①②可知，

\(f(x+2)=-f(-x)\)，即\(f(x+2)+f(-x)=0\)，即对称中心是\((1，0)\)，

这时要么函数在\((1，0)\)处没有定义，这个不满足题意；

要么必有\(f(1)=0\)，则\(f(-1)=0\)；其余就好处理了。

法3：赋值法，由\(f(x)+f(-x)=0\)，令\(x=1\)，得到\(f(1)+f(-1)=0\)①，

令\(x=-1\)，由\(f(x)=f(x+2)\)得到，\(f(-1)=f(1)\)②，

故有\(f(1)=f(-1)=0\)，

在此基础上，做出函数的大致图像，可知\(f(1)=f(2)=f(0)=0\)，

\(f(\cfrac{3}{2})+f(\cfrac{5}{2})=0\)，\(f(\cfrac{1}{2})=\sqrt{2}-1\)，

故\(f(\cfrac{1}{2})+f(1)+f(\cfrac{3}{2})+f(2)+f(\cfrac{5}{2})=\sqrt{2}-1\)。

例6

周期性给定\(f(x+2)=f(x)\)，则可知函数\(f(x)\)的周期为\(T=2\)，那么给定\(f(x-1)=f(x+1)\)，给其中的\(x\)赋值\(x+1\)，变换得到\(f(x)=f(x+2)\)，也说明\(f(x-1)=f(x+1)\)刻画的是周期性，且周期为\(T=2\)；

练习：①\(f(x+1)=f(x+5)\)，则\(T=4\)，说明：给其中的\(x\)赋值\(x-1\)，得到\(f(x)=f(x+4)\)，则\(T=4\)；

②\(f(2-x)=f(4-x)\)，则\(T=2\)，说明：给其中的\(x\)赋值\(-x\)，得到\(f(x+2)=f(x+4)\)，给其中的\(x\)赋值\(x-2\)，得到\(f(x)=f(x+2)\)，则\(T=2\)；

③\(f(x+a)=f(x+b)(a<b)\)，则\(T=b-a\)，说明：给其中的\(x\)赋值\(x-1\)，得到\(f(x)=f(x+4)\)，则\(T=4\)；

3、 求函数的解析式

• 已知定义在\(R\)上的函数\(f(x)\)满足条件\(f(x-y)=f(x)-y(2x-y+1)\)，且\(f(0)=1\)，求\(f(x)\)的解析式；
  

分析：令\(y=x\)，代入原式得到\(f(x-x)=f(x)-x(2x-x+1)\)，

即\(f(0)=f(x)-x(x+1)\)，

即\(f(x)=x^2+x+1\)

• 函数\(f(x)\)对一切实数\(x、y\)均有\(f(x+y)-f(y)=x(x+2y+1)\)成立，且\(f(1)=0\)．求函数\(f(x)\)的解析式．
  

分析：注意到\(f(1)=0\)，故令\(y=1\)，代入原式得到\(f(x+1)-f(1)=x(x+2\times +1)=x^2+3x\)，

即\(f(x+1)=x^2+3x\)，令\(x+1=t\)，则\(x=t-1\)，代入上式，得到\(f(t)=(t-1)^2+3(t-1)=t^2+t-2\)，

即\(f(x)=x^2+x-2\)。

• 已知函数\(f(x)=x^2+2f'(2)\cdot x+1\)，求函数的解析式\(f(x)\).
  

分析：给原式两边同时求导，可得\(f'(x)=2x+2f'(2)\)，

再令\(x=2\)得到\(f'(2)=4+2f'(2)\)，解得\(f'(2)=-4\)，可知\(f(x)=x^2-8x+1\)。

• 已知函数\(f(x)=1+f(\cfrac{1}{2})\cdot log_2x\)，求函数\(f(x)\)的解析式及\(f(2)\)的值。

分析：令\(x=\cfrac{1}{2}\)，则\(f(\cfrac{1}{2})=1+f(\cfrac{1}{2})\cdot log_2\cfrac{1}{2}\)，

即\(f(\cfrac{1}{2})=1-f(\cfrac{1}{2})\)，解得\(f(\cfrac{1}{2})=\cfrac{1}{2}\)，

故所求解析式为\(f(x)=1+\cfrac{1}{2}log_2x\)，

则\(f(2)=1+\cfrac{1}{2}=\cfrac{3}{2}\)。

4、数列中求通项公式

• 如\(a_{n+m}=a_n\cdot a_m\)，\(a_1=2\)，求通项公式\(a_n\)；
  

令\(m=1\)得到\(a_{n+1}=a_n\cdot a_1=a_1\cdot a_n\)，

即\(\cfrac{a_{n+1}}{a_n}=a_1=2\)

不就是等比数列嘛；故\(a_n=2\cdot 2^{n-1}=2^n\)

• 如\(a_{n+m}=a_n+ a_m\)，\(a_1=2\)，求通项公式\(a_n\)；
  

令\(m=1\)得到\(a_{n+1}=a_n+ a_1\)，

即\(a_{n+1}-a_n=a_1=2\)，不就是等差数列嘛；

故\(a_n=2+(n-1)\times 2=2n\)

• 等差数列\(\{a_n\}\)，\(a_n>0\)，且数列\(\{\cfrac{1}{a_na_{n+1}}\}\)的前\(n\)项和为\(\cfrac{n}{2(n+2)}\)，求数列\(\{a_n\}\)的通项公式；

分析：当\(n=1\)时，\(\cfrac{1}{a_1a_2}=\cfrac{1}{2\times3}=\cfrac{1}{6}\)①；

当\(n=2\)时，\(\cfrac{1}{a_1a_2}+\cfrac{1}{a_2a_3}=\cfrac{2}{2\times4}=\cfrac{1}{4}\)②；

①-②得到\(\cfrac{1}{a_2a_3}=\cfrac{1}{12}\)

则有\(a_1\cdot (a_1+d)=6\)③；\((a_1+d)(a_1+2d)=12\)④，

由③④解得\(a_1=2\)，\(d=1\)；故\(a_n=n+1\)；

5、不等式大小比较

设\(0< b < a <1\)，则下列不等式成立的是【】

A、\(ab < b^2<1\;\;\;\;\;\) B、\(log_\frac{1}{2}b < log_\frac{1}{2}a <0\;\;\;\;\;\) C、\(2b < 2a < 2\;\;\;\;\;\) D、\(a^2 < ab <1\;\;\;\;\;\)

【法2】赋值法，由题设令\(b=\cfrac{1}{4}\)，\(a=\cfrac{1}{2}\)，

对选项A而言，\(ab=\cfrac{1}{2}\times \cfrac{1}{4}=\cfrac{1}{8}\)，\(b^2=\cfrac{1}{4}\times \cfrac{1}{4}=\cfrac{1}{16}\)，\(\cfrac{1}{8}>\cfrac{1}{16}\)， 故A错；

对选项B而言，\(log_\frac{1}{2}b=log_\frac{1}{2} \cfrac{1}{4}=2>0\)，故B错；

对选项D而言，\(a^2=(\cfrac{1}{2})^2=\cfrac{1}{4}\) ； $ ab=\cfrac{1}{2}\times \cfrac{1}{4}=\cfrac{1}{8}< a^2$，故D错；

例8-1若\(x\in (e^{-1}，1)\)，\(a=lnx\)，\(b=(\cfrac{1}{2})^{lnx}\)，\(c=e^{lnx}\)，则其大小关系为__________。

分析：借助赋值法，令\(x=\cfrac{1}{2}\)，则可知\(b=(\cfrac{1}{2})^{lnx}>1\)，\(a=lnx<0\)，\(c=e^{lnx}=\cfrac{1}{2}\)，故大小关系为\(b>c>a\)；

6、二项式系数求和

若\((1+x)(a-x)^6=a_0+a_1x+a_2x^2+\cdots+a_7x^7\)，其中\(a=\int_0^{\pi}(sinx-cosx)dx\)，

则\(a_0+a_1+a_2+\cdots+a_6\)的值为__________.

分析：先求得\(a=(-cosx-sinx)|_0^{\pi}=2\)，

代入已知表达式，再赋值\(x=1\)，

得到\(a_0+a_1+a_2+\cdots+a_6+a_7=(1+1)(2-1)^6=2\)，

又\(C_6^6\cdot 2^0\cdot (-x)^6\cdot x=x^7\)，故\(a_7=1\)，

从而解得\(a_0+a_1+a_2+\cdots+a_6=1\).

二项式定理将赋值法的使用发挥到了极致。

相关链接：1、二项式定理； 2、二项式定理的相关习题；

7、集合的关系判断

例10

已知集合\(M=\{x\mid x=\cfrac{k}{2}+\cfrac{1}{4}，k\in Z \}\)，\(N=\{x\mid x=\cfrac{k}{4}+\cfrac{1}{2}，k\in Z \}\)，则两个集合的关系是【】

\(A. N\subsetne M \;\;\;\;\;\) \(B. M\subsetne N \;\;\;\;\;\) \(C. M= N \;\;\;\;\;\) \(D. M\cap N=\varnothing \;\;\;\;\;\)

分析：【法1】赋值法，由于\(k\in Z\)，故我们给\(k\)赋值\(\cdots，-2，-1，0，1，2，\cdots\)，这样就分别得到了两个无限集合了。

\(M=\{\cdots，-\cfrac{3}{4}，-\cfrac{1}{4}，\cfrac{1}{4}，\cfrac{3}{4}，\cfrac{5}{4}，\cfrac{7}{4}，\cdots，\}\)，素之间的间隔为\(\cfrac{2}{4}=\cfrac{1}{2}\)，素少

\(N=\{\cdots，-\cfrac{1}{4}，0，\cfrac{1}{4}，\cfrac{2}{4}，\cfrac{3}{4}，\cfrac{4}{4}，\cdots，\}\)，素之间的间隔为\(\cfrac{1}{4}\)，素多

这样我们就很容易发现关系为\(M\subsetne N\)，故选\(B\)。

【法2】数列法，如果我们经常将数列当成函数来理解，那么我们可以看到，两个无限集合可以看成数列

集合\(M\)的素可以看成公差为\(\cfrac{1}{2}\)，其中某一项为\(\cfrac{1}{4}\)的无穷等差数列，

合\(N\)的素可以看成公差为\(\cfrac{1}{4}\)，其中某一项为\(\cfrac{1}{2}\)的无穷等差数列，

我们画两条平行的数轴，在上面依照两个集合的素取点时，就会发现关系为\(M\subsetne N\)，故选\(B\)。

8、三角函数

已知\(f(x)=2Acos^2(\omega x+\phi)(A>0,\omega>0,0<\phi<\cfrac{\pi}{2})\)，直线\(x=\cfrac{\pi}{3}\)和点\((\cfrac{\pi}{12},0)\)
分别是函数\(f(x)\)图象上相邻的一条对称轴和一个对称中心，求函数\(f(x)\)的解析式。

分析：由\(f(x)=2Acos^2(\omega x+\phi)=A[cos2(\omega x+\phi)+1]-A=Acos(2\omega x+2\phi)\)，

故其周期为\(T=\cfrac{2\pi}{2\omega}=\cfrac{\pi}{\omega}\)，

又由题目可知\(\cfrac{T}{4}=\cfrac{\pi}{3}-\cfrac{\pi}{12}=\cfrac{\pi}{4}\)，则\(T=\pi=\cfrac{\pi}{\omega}\)，

故\(\omega=1\)，则函数简化为\(f(x)=Acos(2x+2\phi)\)，再利用直线\(x=\cfrac{\pi}{3}\)是函数\(f(x)\)图象上的一条对称轴，

故\(2\times \cfrac{\pi}{3}+2\phi=k\pi,(k\in Z)\),解得\(\phi=\cfrac{k\pi}{2}-\cfrac{\pi}{3}\)，

令\(k=1\)，则\(\phi=\cfrac{\pi}{6}\in (0,\cfrac{\pi}{2})\)，满足题意，

故\(f(x)=Acos(2x+2\phi)=Acos(2x+\cfrac{\pi}{3})\).

9、解决抽象函数不等式问题

例12【2019届宝鸡中学高三文科第一次月考第22题】

设函数\(f(x)\)是增函数，对于任意\(x，y\in R\)都有\(f(x+y)=f(x)+f(y)\)，

（1）求\(f(0)\)；

分析：考查赋值法，令\(x=y=0\)，得到\(f(0+0)=f(0)+f(0)\)，即\(f(0)=0\)。

（2）证明函数\(f(x)\)是奇函数；

分析：由题目可知，定义域关于原点对称，

令\(y=-x\)，代入已知得到\(f(x-x)=f(x)+f(-x)\)，即\(f(x)+f(-x)=0\)，

即\(f(-x)=-f(x)\)，故函数\(f(x)\)是奇函数；

（3）解不等式\(\cfrac{1}{2}f(x^2)-f(1-x) <\cfrac{1}{2}f(3x)\)；

分析：先将已知变形为\(f(x^2)-2f(1-x) < f(3x)\)；

再变形为\(f(x^2)-f(3x)< 2f(1-x)\)，

（提示：上式变形的最终形式应该是\(f(M) < f(N)\)的形式，为此需要将\(-f(3x)\)变形，需要将\(2f(1-x)\)变形）

由于任意\(x，y\in R\)都有\(f(x+y)=f(x)+f(y)\)，

令\(x=y\)，得到\(f(2x)=f(x)+f(x)=2f(x)\)，应用到题目中，有\(2f(1-x)=f(2-2x)\)

又\(-f(x)=f(-x)\)，应用到题目中，有\(-f(3x)=f(-3x)\)，

故\(f(x^2)-f(3x)<2f(1-x)\)可以再次变形，得到

\(f(x^2)+f(-3x)< f(2-2x)\)，即\(f(x^2-3x)< f(2-2x)\)，

由于函数\(f(x)\)是\(R\)上的增函数，故由单调性有

\(x^2-3x< 2-2x\)，即\(x^2-x-2<0\)，

解得\(-1< x <2\)，即解集为\(x\in (-1，2)\)。

函数\(f(x)\)对任意的\(m，n\in R\)，都有\(f(m+n)=f(m)+f(n)-1\)，并且\(x>0\)，恒有\(f(x)>1\)。

（1）求证：\(f(x)\)在\(R\)上是增函数；

证明：设\(x_1，x_2\in R\)，且\(x_1 < x_2\)，则\(x_2-x_1 >0\)，

由题目当\(x >0\)，恒有\(f(x) >1\)，则\(f(x_2-x_1)>1\)，

\(f(x_2)=f[(x_2-x_1)+x_1]=f(x_2-x_1)+f(x_1)-1\)

则\(f(x_2)-f(x_1)=f(x_2-x_1)-1>0\)，

故\(f(x_1)< f(x_2)\)，即\(f(x)\)在\(R\)上是增函数；

（2）若\(f(3)=4\)，解不等式\(f(a^2+a-5)<2\)。

分析：\(m，n\in R\)，都有\(f(m+n)=f(m)+f(n)-1\)，

令\(m=n=1\)，则\(f(1+1)=f(1)+f(1)-1\)，即\(f(2)=2f(1)-1\)，

又由已知\(f(3)=4\)，即\(4=f(2+1)=f(2)+f(1)-1\)，

即\(3f(1)-2=4\)，即\(f(1)=2\)，也即\(2=f(1)\)

故\(f(a^2+a-5)<2=f(1)\)，又\(f(x)\)在\(R\)上是增函数；

则有\(a^2+a-5<1\)，解得\(a\in (-3，2)\)。

【解后反思】：解抽象函数不等式的一般步骤：

①(定性)确定函数\(f(x)\)在给定区间上的单调性；

②(转化)将抽象函数不等式转化为\(f(M) < f(N)\)的形式；

③(脱去\(f\))利用单调性去掉函数符号\(\large{f}\)，转化为一般的不等式(组)；

④(求解)求解上述的不等式组；

⑤(反思)反思回顾，查看关键点，易错点及解题规范。OK!

10、公式证明中用到赋值法

① 由\(cos(\alpha-\beta)=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\)，用\(-\beta\)替换\(\beta\)，或者给\(\beta\)赋值\(-\beta\)，

得到\(cos(\alpha+\beta)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\)，

②由\(sin(\alpha+\beta)\)推导\(sin(\alpha-\beta)\)；

③由\(f(x+4)=f(-x)\)等价于\(f(x+3)=f(-x+1)\)；

④由\(a^3+b^3\)推导\(a^3-b^3\)；

11、正态分布中用到赋值法

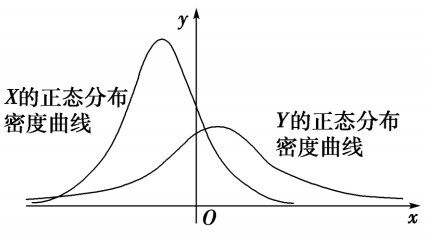
例3【2015·高考湖北卷】设\(X\sim N(\mu_1，\sigma_1^2)\)，\(Y\sim N(\mu_2，\sigma_2^2)\)，这两个正态分布密度曲线如图所示．下列结论中正确的是【】

\(A.P(Y\ge \mu_2)\ge P(Y\ge \mu_1)\)

\(B.P(X\leq \sigma_2)\ge P(X\leq \sigma_1)\)

\(C\).对任意实数\(t\)，\(P(X\leq t)\ge P(Y\leq t)\)

\(D\).对任意实数\(t\)，\(P(X\ge t)\ge P(Y\ge t)\)

分析：根据正态密度曲线可知，\(\mu_1<\mu_2\)，\(\sigma_1<\sigma_2\)，

则有\(P(Y\ge \mu_2)< P(Y\ge \mu_1)\)，故\(A\)错； 且有\(P(X\leq \sigma_2)< P(X\leq \sigma_1)\)，故\(B\)错；

对\(C\)选项而言，不妨赋值，设\(t=\mu_1\)，由图可知，必有\(P(X\leq t)\ge P(Y\leq t)\)，故\(C\)正确；

对\(D\)选项而言，不妨赋值，设\(t=\mu_1\)，由图可知，必有\(P(X\ge t)< P(Y\ge t)\)，故\(D\)错误；

综上所述，选\(C\)。