geohash简介文章参见
地理空间索引:GeoHash原理
优化线段的编码效率参见
地理空间索引:线段的GeoHash编码优化
在上一篇博客地理空间索引:GeoHash原理中,我们讨论了如何将一个经纬度坐标转化为GeoHash编码,但是出于很多工作上的需要,我们需要在此基础上对线段与多边形进行编码,本文就探讨这个话题。
1. 编码直线与多边形
这里首先规定一下线段和多边形的输入格式:
- 线段:用起点和终点的经纬度表示,
[(108.940430, 34.343436), (116.411133, 39.909736)] - 多边形:用围绕多边形的顶点经纬度表示,相邻顶点的连线是多边形的一条边,首尾顶点重合,
[(108.940430, 34.343436), (116.411133, 39.909736), (120.168457, 30.278044), (114.323730, 30.581179), (108.940430, 34.343436)]
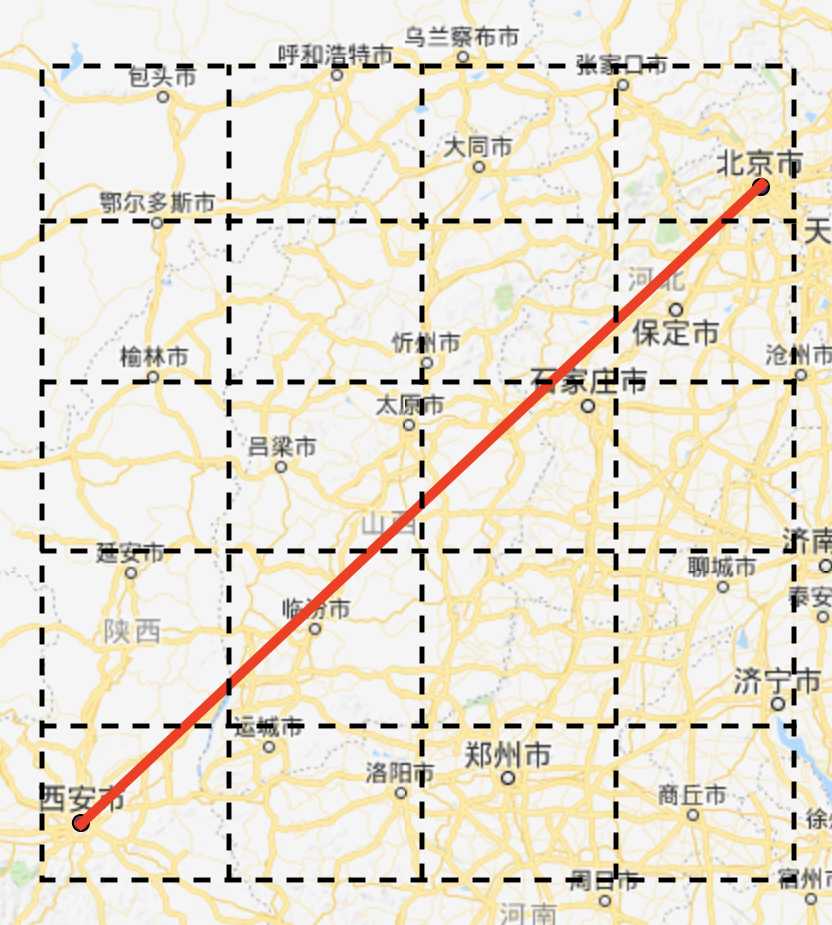 图1 线段 图1 线段 |
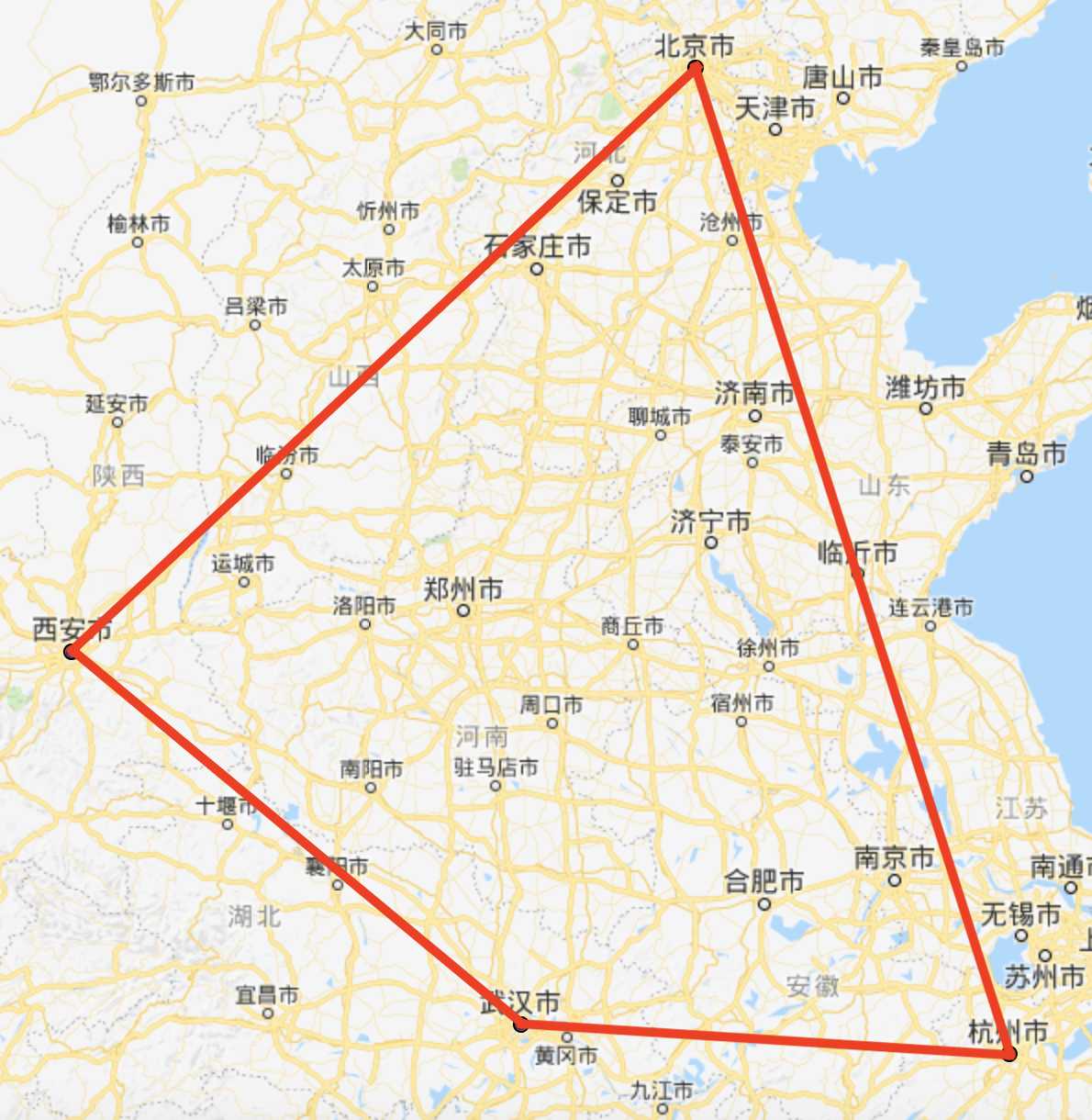 图2 多边形 图2 多边形 |
实际上多边形的边就是线段,与线段的编码一致,只不过多边形内部也需要编码,因此首先讨论线段的编码方式。
在同一编码长度下,GeoHash将地图打上同尺寸的矩形网格,那么一条线段所穿过所有网格的hash值集合就是该线段GeoHash编码结果。根据这个思路,我们首先将线段所在的外包矩形bbox(Bounding box)找到,将bbox按照GeoHash编码打上网格,然后判断每个网格是否被线段穿过。因为网格是矩形,线段穿过矩形只有两种情况:线段与矩形的边相交,或线段在矩形内部。由此可见,我们需要从更基本的判定方法进行准备。
2. 基本几何相交的判定方法
首先我们定义好点和线段的Python类方便后续代码实现,Point类具有经纬度坐标,同时可以比较大小;Line类具有起终点,同时具有向量的坐标。同时我们定义了向量的叉乘和点乘便于后续使用。
class Point(object):
def __init__(self, x, y):
self.x, self.y = float(x), float(y)
def __lt__(self, other):
if self.x != other.x:
return self.x < other.x
return self.y < other.y
def __eq__(self, other):
return self.x == other.x and self.y == other.y
class Line(object):
def __init__(self, start, end):
self.start, self.end = start, end
self.x = end.x - start.x
self.y = end.y - start.y
def cross_product(line1, line2):
return line1.x * line2.y - line2.x * line1.y
def dot_product(line1, line2):
return line1.x * line2.x + line1.y * line2.y
1.1 判定两条线段相交
两条线段之间的关系可以分别通过快速排斥实验和跨立实验进行确定:互相排斥的线段,以它们为对角线的矩形没有重合(如图3);互相跨立的线段,以它们为对角线的矩形有重合,且两线段有交点(如图4)。
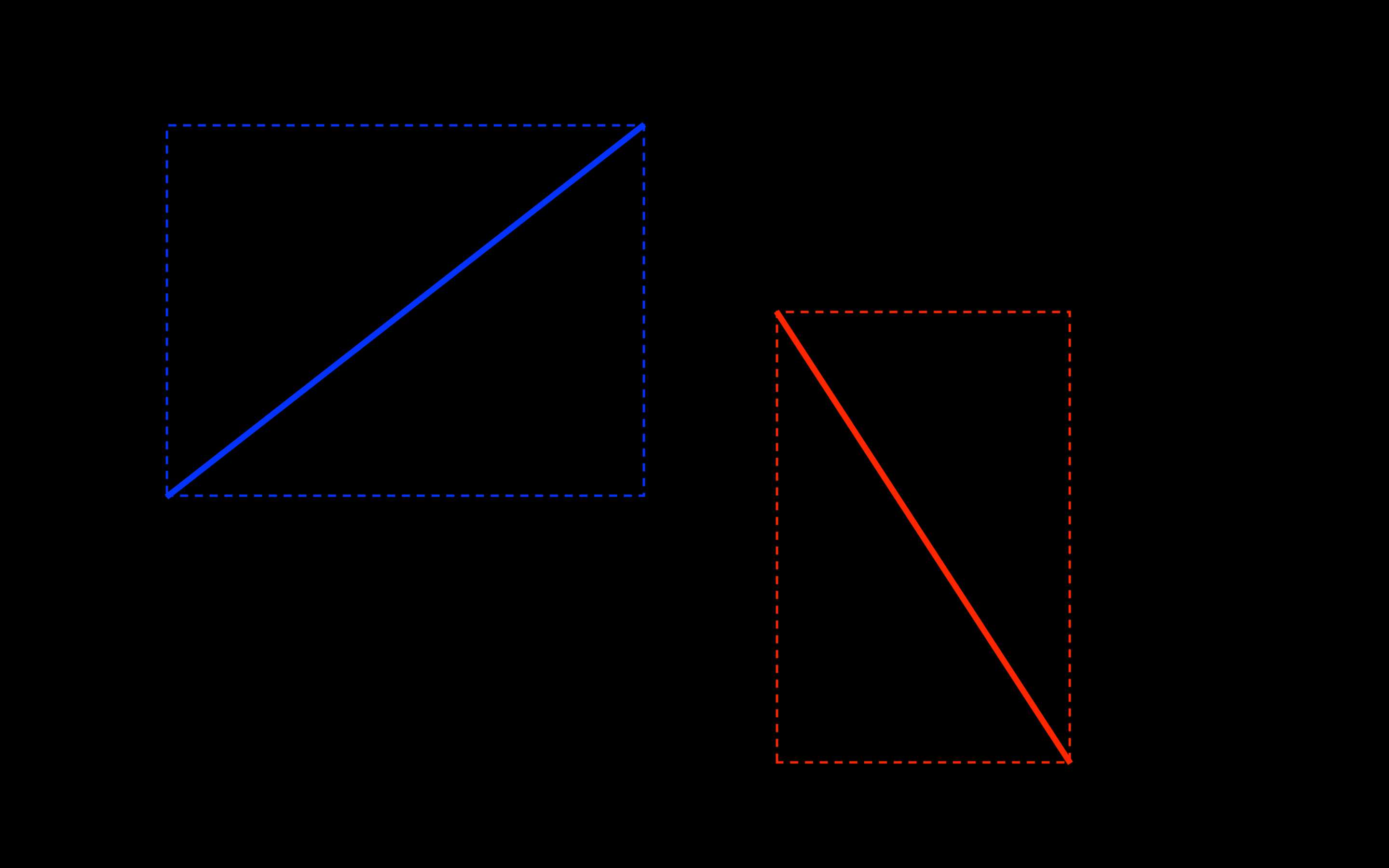 图3 排斥 图3 排斥 |
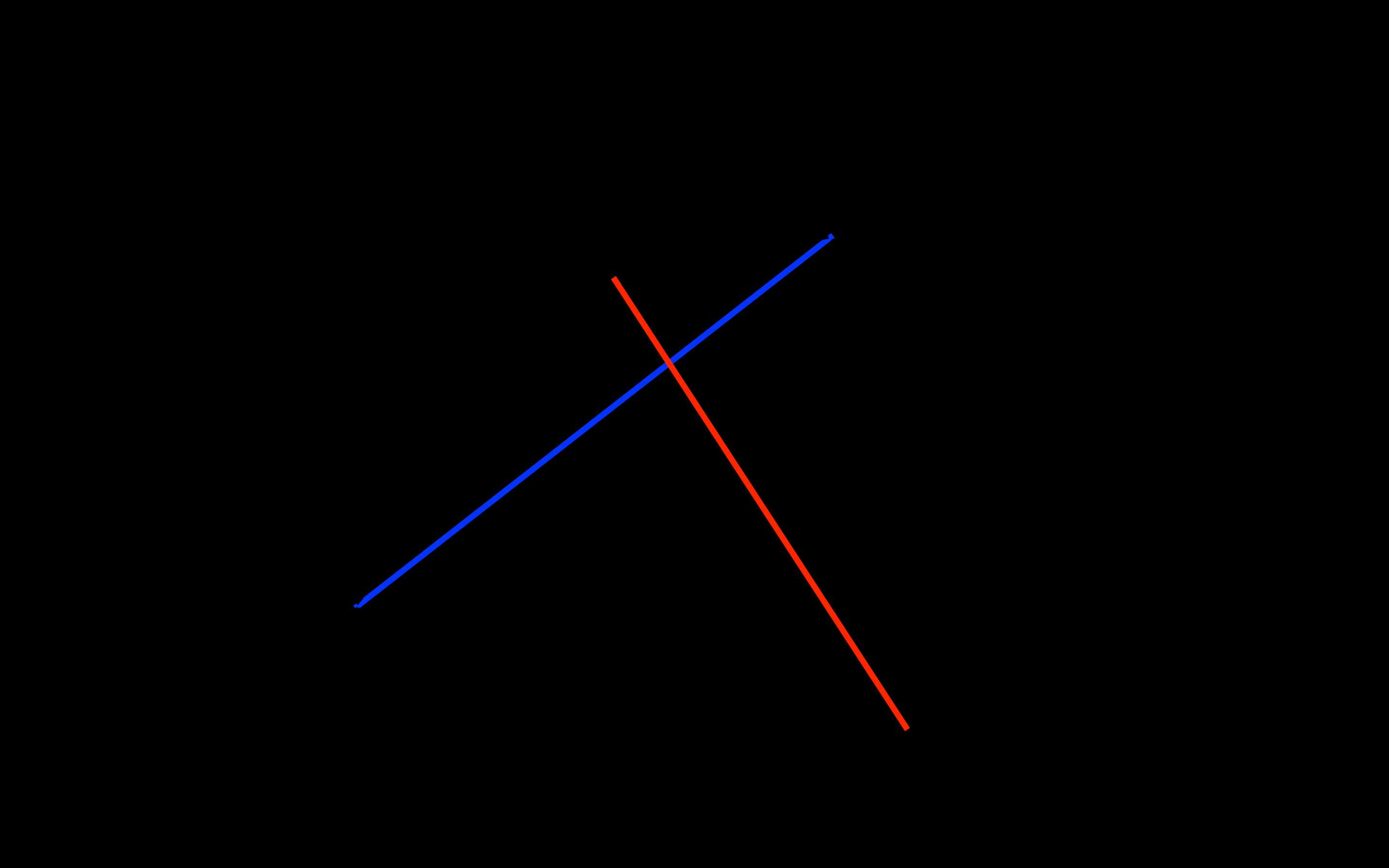 图4 跨立 图4 跨立 |
对图3中互相排斥的线段AB和CD,其关系可以根据其为对角线的矩形来判定:
def is_included(line1, line2):
return min(line1.start.x, line1.end.x) <= max(line2.start.x, line2.end.x) and \
min(line2.start.x, line2.end.x) <= max(line1.start.x, line1.end.x) and \
min(line1.start.y, line1.end.y) <= max(line2.start.y, line2.end.y) and \
min(line2.start.y, line2.end.y) <= max(line1.start.y, line1.end.y)
对图4中互相跨立的线段AB和CD,向量AC、AD以及BC、BD一定分居线段AB两侧;向量AC、BC以及AD、BD一定分居线段CD两侧,判定跨立则可以通过向量叉乘的符号来判定:
def is_crossed(line_ab, line_cd):
line_ac = Line(line_ab.start, line_cd.start)
line_ad = Line(line_ab.start, line_cd.end)
line_bc = Line(line_ab.end, line_cd.start)
line_bd = Line(line_ab.end, line_cd.end)
return cross_product(line_ac, line_ad) * cross_product(line_bc, line_bd) <= 0 and \
cross_product(line_ac, line_bc) * cross_product(line_ad, line_bd) <= 0
从而
def is_lines_intersected(line_ab, line_cd):
return is_included(line1, line2) and is_crossed(line_ab, line_cd)
1.2 判定线段与矩形相交
线段与矩形相交,要么线段与矩形的4条边相交,要么线段在矩形内部。在这里我们定义矩形为字典rect = {'w': min_x, 'e': max_x, 's': min_y, 'n': max_y},定义矩形的边为字典rect_sides = {'w': west_line, 'e': east_line, 's': south_line, 'n': north_line}。为了加快运算速度,我们记录下了矩形每条边与线段的相交情况,具体标记在下一节解释。
def is_rect_has_intersected_side(rect_sides):
return any(map(lambda side: side[1] == 1, rect_sides.values()))
def is_point_within_rect(point, rect):
return rect['w'] <= point.x <= rect['e'] and rect['s'] <= point.y <= rect['n']
def is_line_rect_intersected(line, rect, rect_sides):
if is_point_within_rect(line.start, rect) or is_point_within_rect(line.end, rect):
return True
for k, side in rect_sides.iteritems():
if side[1] == -1 and is_lines_intersected(line, side[0]):
rect_sides[k][1] = 1
return is_rect_has_intersected_side(rect_sides)
3. 线段的GeoHash编码
在基本判定方法齐全后,我们终于可以设计线段的GeoHash编码了。我们将线段的外包矩形找到,以外包矩形的西(w)南(s)点坐标作为种子点进行GeoHash编码,并按照该编码的经纬度间隔向地图上打网格,并要求完全涵盖外包矩形。接着只需要挨个判定规定线段是否和网格矩形相交,记录下相交矩形的GeoHash编码就完成了线段的编码。
接下来有一个优化点:因为网格里的边是固定的,但我们是按照逐个网格矩形来判定的,因此会有网格内部的边都会被判断两遍。为了节省重复计算,我们将网格所有的边以及它们与线段的相交情况全部记录下来并不断更新。相交情况分为三种1:已判定相交,0:已判定不相交和-1:未判定,那么初始化时网格外边缘记录为0,而内部边记录为-1,每次只需要对标记为-1的未判定的边进行判定即可。
import numpy as np
import geohash
def bounding_rect(line_points_list):
north = east = 0.
south = west = np.inf
for lng, lat in line_points_list:
if lat > north: north = lat
if lat < south: south = lat
if lng > east: east = lng
if lng < west: west = lng
return {
'w': west, 'e': east, 'n': north, 's': south}
def init_grid_lines(lng_list, lat_list):
n_lng, n_lat = len(lng_list), len(lat_list)
lng_lines_list = []
for i in xrange(n_lng):
lng = lng_list[i]
sign = 0 if i == 0 or i == n_lng - 1 else -1
line_list = [[Line(Point(lng, lat_list[j]), Point(lng, lat_list[j + 1])), sign]
for j in xrange(n_lat - 1)]
lng_lines_list.append(line_list)
lat_lines_list = []
for i in xrange(n_lat):
lat = lat_list[i]
sign = 0 if i == 0 or i == n_lat - 1 else -1
line_list = [[Line(Point(lng_list[j], lat), Point(lng_list[j + 1], lat)), sign]
for j in xrange(n_lng - 1)]
lat_lines_list.append(line_list)
return lng_lines_list, lat_lines_list
def get_rect(rect_sides): # 辅助函数,由rect_sides获取rect
start, end = rect_sides['w'][0].start, rect_sides['e'][0].end
return {
'w': start.x, 'e': end.x, 's': start.y, 'n': end.y}
def line_to_geohash(line_points_list, precision):
rect = bounding_rect(line_points_list)
seed_code = geohash.encode(rect['s'], rect['w'], precision)
seed_bbox = geohash.bbox(seed_code)
lng_delta, lat_delta = seed_bbox['e'] - seed_bbox['w'], seed_bbox['n'] - seed_bbox['s']
lng_list = np.arange(seed_bbox['w'], rect['e'] + lng_delta, lng_delta)
lat_list = np.arange(seed_bbox['s'], rect['n'] + lat_delta, lat_delta)
lng_lines_list, lat_lines_list = init_grid_lines(lng_list, lat_list)
hash_list = []
for i in xrange(len(lng_lines_list) - 1):
for j in xrange(len(lat_lines_list) - 1):
west_line, east_line = lng_lines_list[i][j], lng_lines_list[i + 1][j]
south_line, north_line = lat_lines_list[j][i], lat_lines_list[j + 1][i]
rect_sides = {
'w': west_line, 'e': east_line, 's': south_line, 'n': north_line}
rect = get_rect(rect_sides)
if is_line_rect_intersected(rect, rect_sides, line_points_list):
center_lat, center_lng = rect['s'] + rect['n']) / 2, (rect['w'] + rect['e']) / 2
hash_list.append(geohash.encode((center_lat, center_lng, precision))
return hash_list
4. 多边形的GeoHash编码
完成了直线的GeoHash编码,我们再考虑多边形的GeoHash编码。按照上面的思路,我们只需要替换线段矩形相交is_line_rect_intersected为多边形矩形相交is_poly_rect_intersected,同时多边形内部也需要进行编码。我们先从最基本的判定开始。
4.1 判定多边形与矩形相交
多边形是由多个线段来表示的,所以可以逐段判断的方法来确定多边形与矩阵相交情况。
def is_poly_rect_intersected(poly_points_list, rect, rect_sides):
for i in xrange(len(poly_points_list) - 1):
line = to_line(poly_points_list[i], poly_points_list[i + 1])
if is_line_rect_intersected(line, rect, rect_sides): return True
return False
4.2 判定点在多边形内
这里采用经典的射线法,核心思路是从点向X轴无穷远方向发射一条射线,多边形与射线的交点数为奇数则点在多边形内,为偶数则点在多边形外,因为参考资料比较多,这里不再赘述。
def is_ray_intersected(point, start, end):
if start[0] <= point[0] and end[0] <= point[0]: return False # ray left
if start[1] >= point[1] and end[1] >= point[1]: return False # ray up
if end[1] < point[1] and start[1] < point[1]: return False # ray down
x_seg = end[0] - (end[0] - start[0]) * (end[1] - point[1]) / (end[1] - start[1]) # intersect point
if x_seg < point[0]: return False # intersected ray left
return True
def is_point_within_poly(point, poly_points_list):
intersected = False
length = len(poly_points_list)
for i in xrange(length - 1):
if is_ray_intersected(point, poly_points_list[i], poly_points_list[i + 1]):
intersected = not intersected
return intersected
4.3 判定矩形在多边形内
矩形的任意一个顶点在多边形内即认为矩形在多边形内
def is_rect_within_poly(rect, poly_points_list):
if is_point_within_poly((rect['w'], rect['s']), poly_points_list): return True
if is_point_within_poly((rect['w'], rect['n']), poly_points_list): return True
if is_point_within_poly((rect['e'], rect['s']), poly_points_list): return True
if is_point_within_poly((rect['e'], rect['n']), poly_points_list): return True
return False
4.4 最后
def poly_to_geohash(poly_points_list, precision):
rect = bounding_rect(poly_points_list)
seed_code = geohash.encode(rect['s'], rect['w'], precision)
seed_bbox = geohash.bbox(seed_code)
lng_delta, lat_delta = seed_bbox['e'] - seed_bbox['w'], seed_bbox['n'] - seed_bbox['s']
lng_list = np.arange(seed_bbox['w'], rect['e'] + lng_delta, lng_delta)
lat_list = np.arange(seed_bbox['s'], rect['n'] + lat_delta, lat_delta)
lng_lines_list, lat_lines_list = init_grid_lines(lng_list, lat_list)
hash_list = []
for i in xrange(len(lng_lines_list) - 1):
for j in xrange(len(lat_lines_list) - 1):
west_line, east_line = lng_lines_list[i][j], lng_lines_list[i + 1][j]
south_line, north_line = lat_lines_list[j][i], lat_lines_list[j + 1][i]
rect_sides = {
'w': west_line, 'e': east_line, 's': south_line, 'n': north_line}
rect = get_rect(rect_sides)
if is_poly_rect_intersected(poly_points_list, rect, rect_sides) or \
is_rect_within_poly(rect, poly_points_list):
center_lat, center_lng = rect['s'] + rect['n']) / 2, (rect['w'] + rect['e']) / 2
hash_list.append(geohash.encode((center_lat, center_lng, precision))
return hash_list
5. 考虑优化
在这种打网格寻找GeoHash的框架下,对于线段的编码效率比较低下,后续我们会对线段的GeoHash编码方式进行改进,效率可以提升2个数量级!
今天的文章地理空间索引:线段与多边形的GeoHash编码分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/13345.html
