什么是Meshgrid以及如何在python中创建和使用它

这篇文章将展示什么是Meshgrid以及如何在python中创建和使用它。

meshgrid是一个由坐标向量组成的矩形数值网格。
假设你想用坐标向量x和y创建一个Meshgrid。天真的方法是创建一个新的矩形网格，并通过在Meshgrid的每个点上评估函数来分配网格的值。下面的代码说明了这种天真的方法。

Meshgrid 天真方式:

x = [0, 1, 2, 3, 4, 5]
y = [0, 1, 2, 3, 4, 5]
z = [[0 for j in range(len(y))] for i in range(x)]
for i in range(len(x)):
    for j in range(len(y)):
        z[i, j] = func(x[i], y[i])

这种方法的缺点是比较繁琐，而且处理大的坐标向量需要更多的时间。用于科学计算的python库numpy有助于更有效地创建网格。为了创建网格，我们将使用函数numpy.meshgrid。下面是使用numpy的相同解决方案。

$ python3
Python 3.8.5 (default, Mar  8 2021, 13:02:45)
[GCC 9.3.0] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import numpy as np
>>> x = np.linspace(0, 6, 3)
>>> x
array([0., 3., 6.])
>>> y = np.linspace(1, 7, 3)
>>> y
array([1., 4., 7.])
>>> xx, yy = np.meshgrid(x, y)
>>> xx
array([[0., 3., 6.],
    [0., 3., 6.],
    [0., 3., 6.]])
>>> xx.shape
(3, 3)

Numpy的矢量操作使其比Python循环更快。矢量化有助于将循环操作委托给内部高度优化的C代码，使其更快。它还表达了对整个数组的操作，而不是数组中的单个元素。

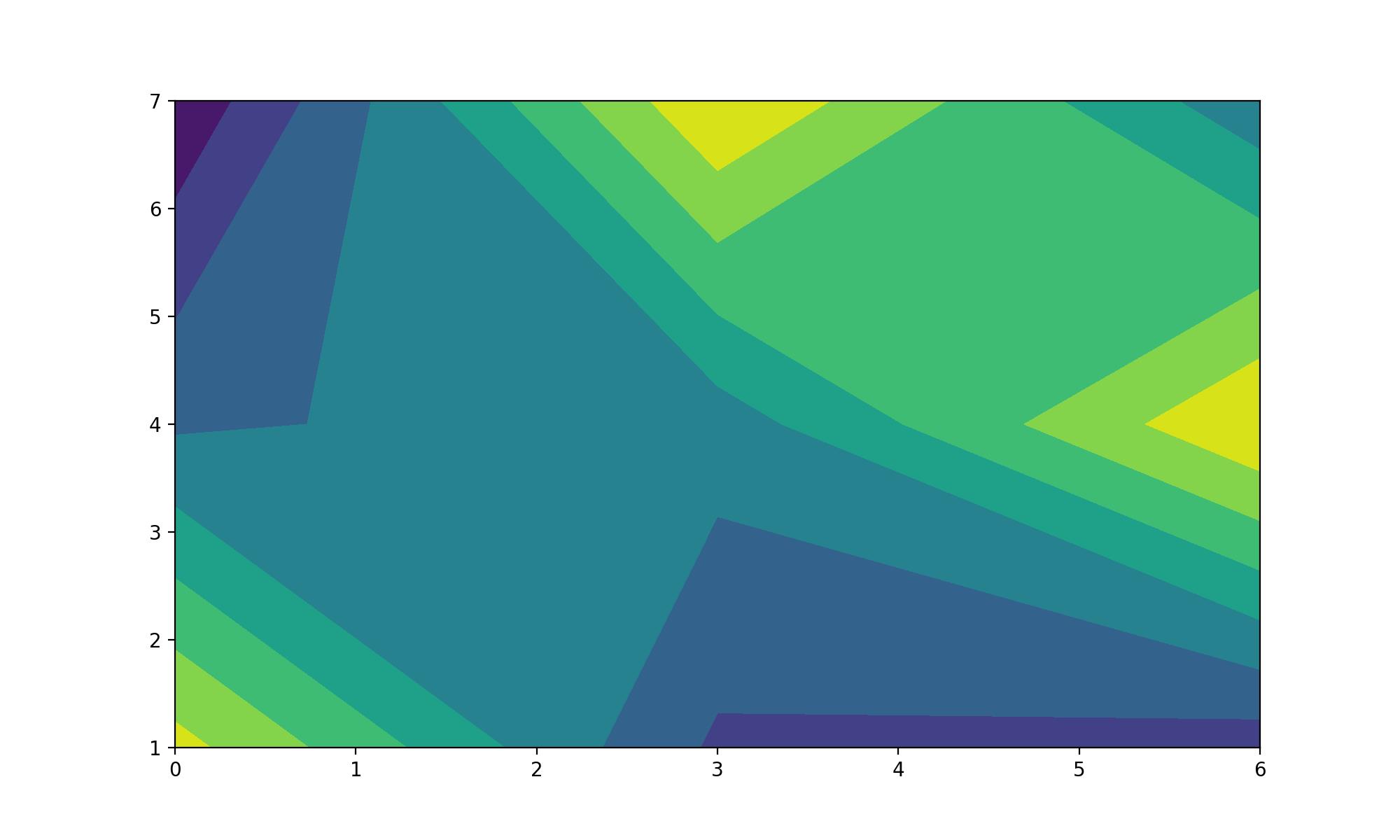
在Meshgrid上评估一个函数是非常容易的。我们所需要做的就是调用函数。我们还将在这里通过使用matplotlib制作一个等高线图来绘制被评估的函数。继续前面的例子。

>>> z = np.sin(xx**2 + yy**2)
>>> import matplotlib.pyplot as plt
>>> plt.figure(figsize=(10, 6))
>>> plt.contourf(xx, yy, z)
>>> plt.colorbar()
>>> plt.show()

如果数组x和y太大，那么数组xx和yy可能会占用大量的空间。这可以用选项sparse=True来优化。

>>> x = np.linspace(0, 5, 6)
>>> y = np.linspace(0, 5, 6)
>>> xx, yy = np.meshgrid(x, y, sparse=False) #default
>>> xx
array([[0., 1., 2., 3., 4., 5.],
    [0., 1., 2., 3., 4., 5.],
    [0., 1., 2., 3., 4., 5.],
    [0., 1., 2., 3., 4., 5.],
    [0., 1., 2., 3., 4., 5.],
    [0., 1., 2., 3., 4., 5.]])
>>> xx.shape
(6, 6)

>>> xx, yy = np.meshgrid(x, y, sparse=True) #default
>>> xx
array([[0., 1., 2., 3., 4., 5.]])
>>> xx.shape
(1, 6)