标题党一次～ 😼

本文首发于 www.shaotianyu.com/article/5ec…

目标是把自己知道的东西讲清楚

1 基本的二分法是什么样子的

二分法的使用场景，其实比较受限，最明显的特点是：

• 绝大情况，查找目标具有单调性质（单调递增、单调递减）
• 有上下边界，并且最好能够通过index下标访问元素

1.1 从头开始，基本的二分法使用

我们从一个最简单的单调递增数组开始说起，问题如下：

在 [1, 2, 3, 4, 5, 6, 7, 8, 9] 中找到 4，若存在则返回下标，不存在返回-1，要求算法复杂度O(logn)

看到上面这题目，O(logn)复杂度的要求，第一反应就是使用二分查找法，怎么做呢？

先在图上模拟以下二分法的大概流程：

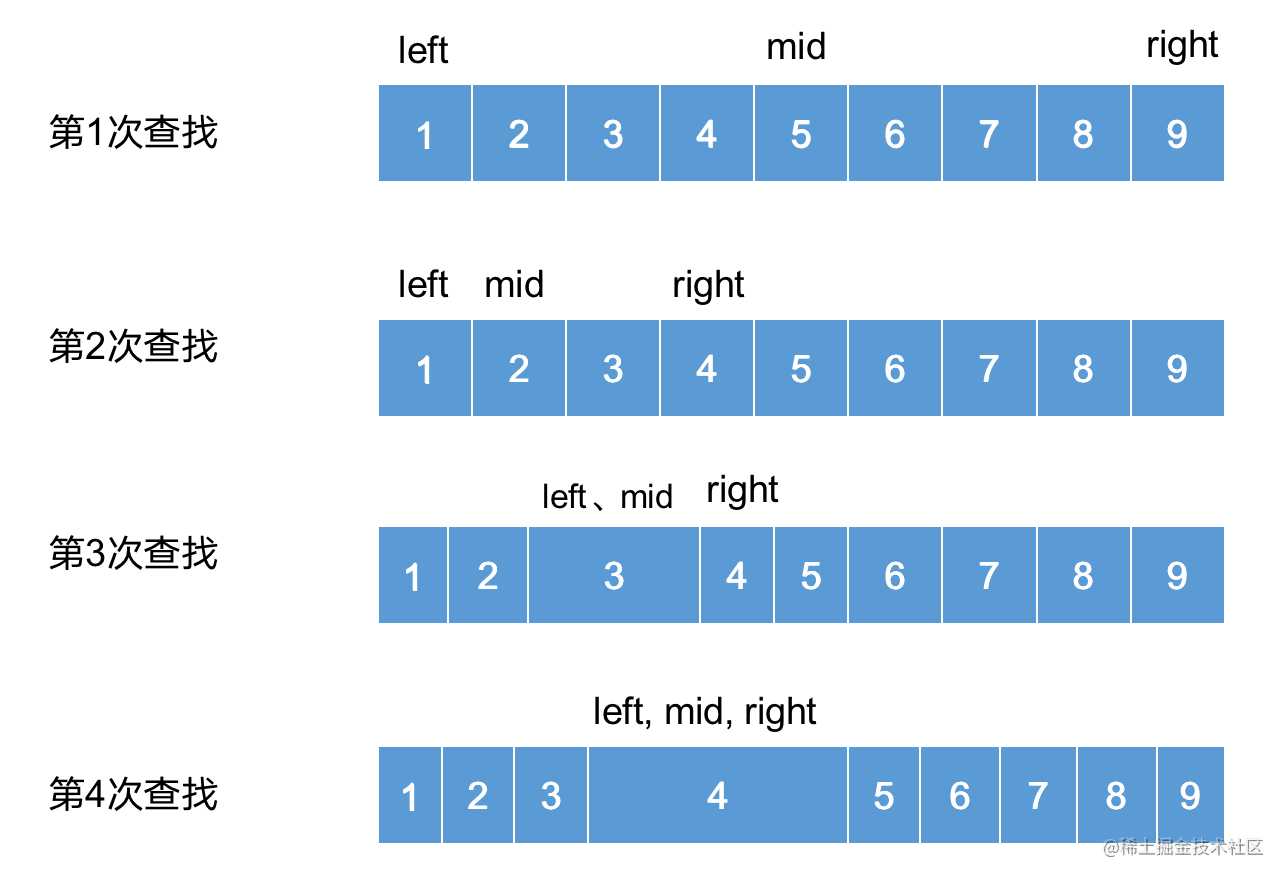
根据图解，代码如下：

function searchNum (target, nums) {
  if (!nums.length) return -1
  let left = 0
  let right = nums.length - 1
  let mid
  while (left <= right) {
      // >> 1 位运算代替 除2 取整 操作
      // 为什么不写成 mid = (left+right)/2 ,因为考虑到left+right的溢出边界情况
      mid = left + ((right - left) >> 1)
      if (nums[mid] === target) {
          return mid
      }
      if (nums[mid] < target) {
          left = mid + 1
      }
      if (nums[mid] > target) {
          right = mid - 1
      }
  }
  return -1
}

1.2 小结二分法的套路

我们可以从上面的问题中，看出点二分法的套路出来，二分法是有律可循的，并且可以推导出基础的模板：

let left = start
let right = end
let mid
while (left <= right) {
    mid = (left + right) / 2
    if (array[mid] === target) {
        return result 或者 break down
    }
    if (array[mid] < target) {
        left = mid + 1
    }
    if (array[mid] > target) {
        right = mid - 1
    }
}

我们得到二分法的基础模板后，就可以顺势解决 x的平方根 这种类型的题目了～

附上 x的平方根 解题代码：

const mySqrt = function(x) {
     if (x < 2) return x
     let left = 1, mid, right = Math.floor(x / 2);
     while (left <= right) {
        mid = Math.floor(left + (right - left) / 2)
        if (mid * mid === x) return mid
        if (mid * mid < x) {
            left = mid + 1
        }else {
            right = mid - 1
        }
     }
     return right
}

2 二分法的扩展

上面说过，二分法的特性之一是，存在明显单调性。这样的话，我们的二分法模板才有用武之地，可是事实上总会存在特殊的情况。

2.1 旋转数组系列 I

题目链接：寻找旋转排序数组中的最小值

题目描述：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。你可以假设数组中不存在重复元素。

解法分析：

• 1、暴力求解，遍历数组，记录最小值，时间复杂度是 O(N)，N是给定数组的大小
• 2、二分法，时间复杂度是 O(logN)，

我们这里怎么使用二分法呢？如何去恰当地利用二分法的特性？如何改进一贯的二分法？

2.1.1 撕开旋转数组的外衣，解析它的规律

首先分解一下题目，题目的前提条件是 升序排序、在未知的某个点旋转，这样的话我们就要首先考虑到，如何判断这个数组最后是升序排列还是已经被旋转打乱顺序？ 我们先画个图看一下：

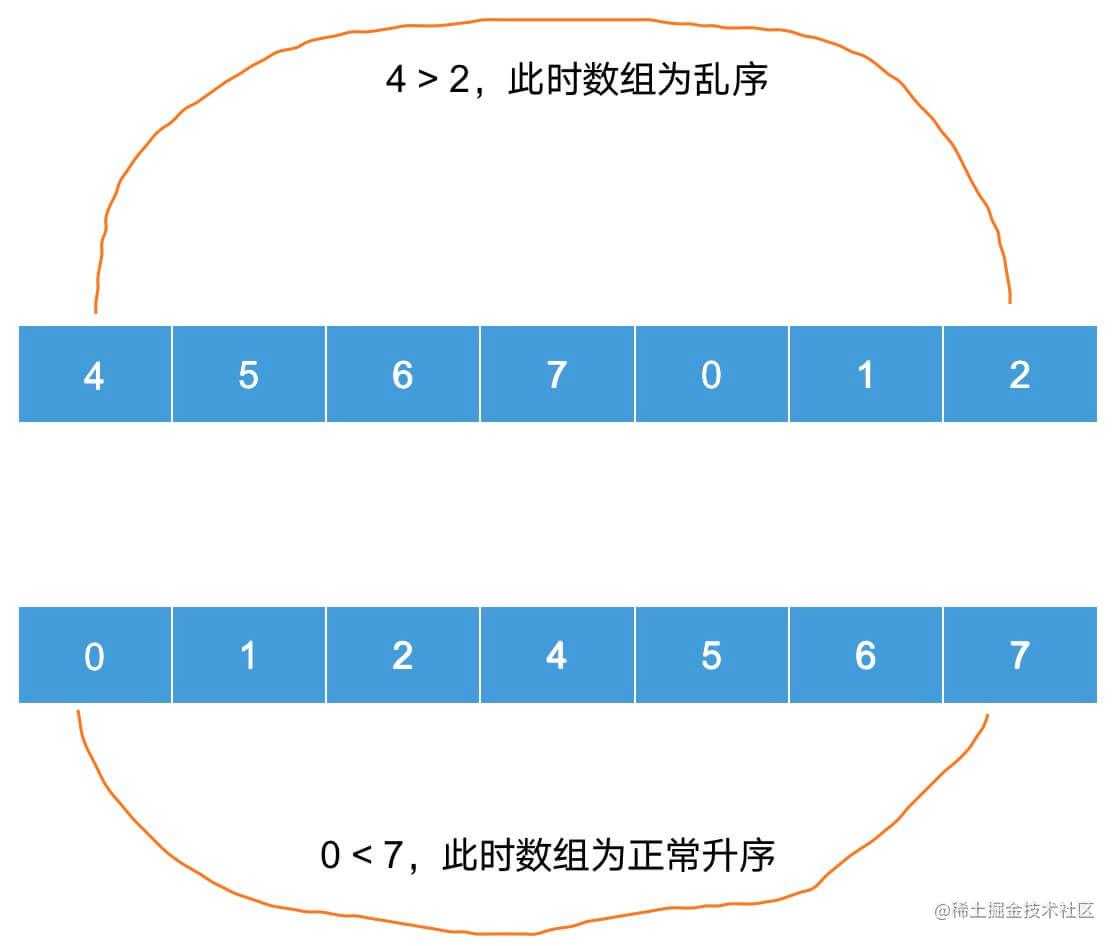
根据上面的图，我们可以直观看出一个规律，如何判断是不是被旋转打乱了？正常升序的前提条件是 first element < last element，而乱序的条件则是：first element > last element

然后再继续挖掘一下乱序数组的规律，那就是乱中有序，如何理解呢 ？

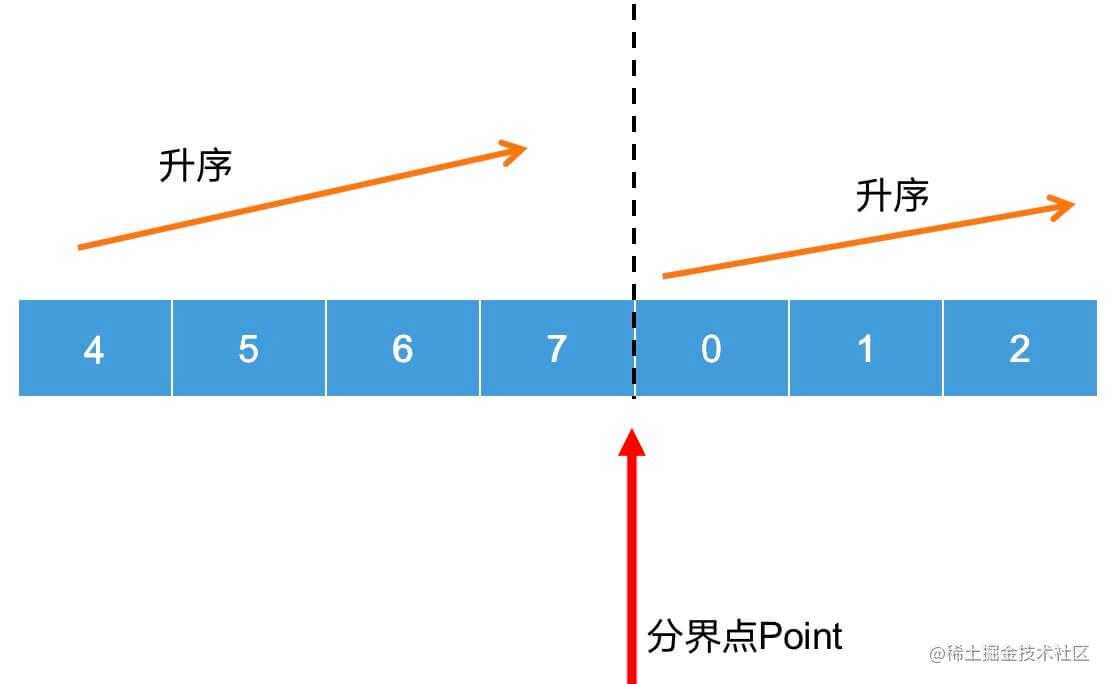
发现了没有，在以黑色虚线为分界点的左右两侧，都是分别升序的，而黑色虚线所在的那个分界点，也就是红色箭头指向的那个 Point，我们可以理解它为 分界点，用来分界两个升序数组。

所以我们可以总结以下规律：

• 1、分界点的左侧元素 >= 第一个元素
• 2、分界点的右侧元素 < 第一个元素

回到问题本身，我们的出发点是要找数组中的最小值，现在看来，我们可以找什么？我们可以找分界点，分界点找到了，最小值就在分界点的旁边，最小值就顺便找到了。

问题的关键找到了，怎么找分界点呢 ？

思路：

第一步：基于二分法的思路，先找mid

第二步：若mid > first element ，说明什么？说明mid的左侧是升序，最小值肯定不在mid左边，此时，我们需要在mid的右边找，所以 left = mid + 1

第三步：若mid < first element ，说明什么？说明最小值肯定在mid左边，此时，我们需要在mid的左边找，所以 right = mid – 1

第四步：终止条件是什么？分两种情况讨论：

• 1、若mid > mid + 1，此时mid + 1就是最小值，返回结果
• 2、若mid < mid – 1，此时mid就是最小值，返回结果

整体思路清楚了，代码就简单了：

const findMin = function (nums) {
    if(!nums.length) return null
    if(nums.length === 1) return nums[0]
    let left = 0, right = nums.length - 1, mid
    // 此时数组单调递增，first element就是最小值
    if (nums[right] > nums[left]) return nums[0]
    while (left <= right) {
        mid = left + ((right - left) >> 1)
        if (nums[mid] > nums[mid + 1]) {
            return nums[mid + 1]
        }
        if (nums[mid] < nums[mid - 1]) {
            return nums[mid]
        }
        if (nums[mid] > nums[0]) {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    return null
}

2.2 旋转数组系列 II

题目链接：搜索旋转排序数组

题目描述：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。你可以假设数组中不存在重复的元素。 你的算法时间复杂度必须是 O(log n) 级别。

算法时间复杂度必须是 O(log n) 级别，二分查找。

这个题目，和上面的很类似，是一类题目，这个题目的解法也有很多种，下面是比较常见的2种：

• 1、根据2.1的最小值的索引，将数组分为两部分有序的数组，再根据num[0]和target的比较关系确定target在分界点的左侧还是右侧，然后在对应的一侧升序数组进行二分查找
• 2、直接对数组进行二分查找，然后在查找中确定分界点的边界关系

如果使用方法2，怎么在二分查找的时候确定边界呢？

由上面2.1中，可以得知，

若mid > first element，说明mid的左侧是升序的；若mid < first element，说明mid的右侧是升序的，而我们通过这规律，就可以区分两段升序的数组，然后在对应的升序区间内，进行二分查找，然后不断调整left和right的位置

我们可以先写一下本道题的思路，思路清楚了，代码就简单了：

思路：

第一步：基于二分法的思路，先找mid

第二步：判断mid 和 first element的大小关系，确立mid所在的区间

第三步：分两部分讨论：

• 在左侧升序区间中，若target >= left 同时 target < mid, 说明target在mid的左侧，应该在[left, mid]之间找，此时执行right = mid – 1；否则target在mid的右侧，在[mid, right]之间找， 此时left = mid + 1;
• 在右侧升序区间中，若target > mid 同时 target <= right , 说明target在mid的右侧，应该在[mid, right]之间找，此时执行left = mid + 1；否则target在mid的左侧，应该在[left, mid]之间找，此时right = mid -1
• 终止条件是，mid element === target，结束

const search = function(nums, target) {
    if (!nums.length) return -1
    let left = 0, right = nums.length - 1, mid
    while (left <= right) {
        mid = left + ((right - left) >> 1)
        if (nums[mid] === target) {
            return mid
        }
        if (nums[mid] >= nums[left]) {
            if (target >= nums[left] && target < nums[mid]) {
                right = mid - 1
            } else {
                left = mid + 1
            }
        } else {
            if (target > nums[mid] && target <= nums[right]) {
                left = mid + 1
            } else {
                right = mid - 1
            }
        }
    }
    return -1
}

2.3 旋转数组系列 III

题目链接：搜索旋转排序数组 II

题目描述：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true，否则返回 false。

这个题目是2.2的变形，思路类似。

不同的点在于这里的数组是含有重复元素的，我们怎么排除重复元素的干扰呢？比如[1,3,1,1,1]这种的数组，很难通过mid和left element的比较界定两个升序区间，不过我们可以通过不断比较mid和left是否相同，来排除重复的干扰项。

思路

若 mid element === left element:
    此时说明具有重复项目，应该调整left指针，使left向右移动，用以去除重复干扰

将上面的思路转化为代码，加入到2.2里面，就可以得到这道题的解：

const search = function(nums, target) {
    if (!nums.length) return false
    let left = 0, right = nums.length - 1, mid
    while (left <= right) {
        mid = left + ((right - left) >> 1)
        if (nums[mid] === target) {
            return true
        }
        if (nums[left] === nums[mid]) {
            ++left
            continue
        }
        if (nums[mid] >= nums[left]) {
            if (target >= nums[left] && target < nums[mid]) {
                right = mid - 1
            } else {
                left = mid + 1
            }
        } else {
            if (target > nums[mid] && target <= nums[right]) {
                left = mid + 1
            } else {
                right = mid - 1
            }
        }
    }
    return false
}

成功AC~

执行用时 :56 ms, 在所有 JavaScript 提交中击败了98.31%的用户

3 小结

上面是对二分法的基础使用案例，和旋转数组系列的基本套路做了一次小汇总，二分法还有很多经典的案例，后续会不断补充。

个人能力有限，若有不足，还望指出。3Q。