树的定义及术语_简述计算之树的定义

树（tree）的定义

简单讲:树就是树,是颜色不一样的烟火…(手动微笑)

关于树的术语(摘自百度百科)

http://baike.baidu.com/link?url=g8V1zMAkQ9cMVxsUJZZpJRT0iBkinqBJWqOUl789tfC3ufE4KvrsHfmwv-2phN9uSYfSeOuAU3QIXvZ2uSTbE2zOFbS55yPr1vc6uU3xHPa

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 叶节点或终端节点：度为0的节点称为叶节点；
• 非终端节点或分支节点：度不为0的节点；
• 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 树的度：一棵树中，最大的节点的度称为树的度；
• 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
• 树的高度或深度：树中节点的最大层次；
• 堂兄弟节点：双亲在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 森林：由m（m>=0）棵互不相交的树的集合称为森林；

完全二叉树

定义

先看二叉树:二叉树是指每个节点只能有两个子节点.
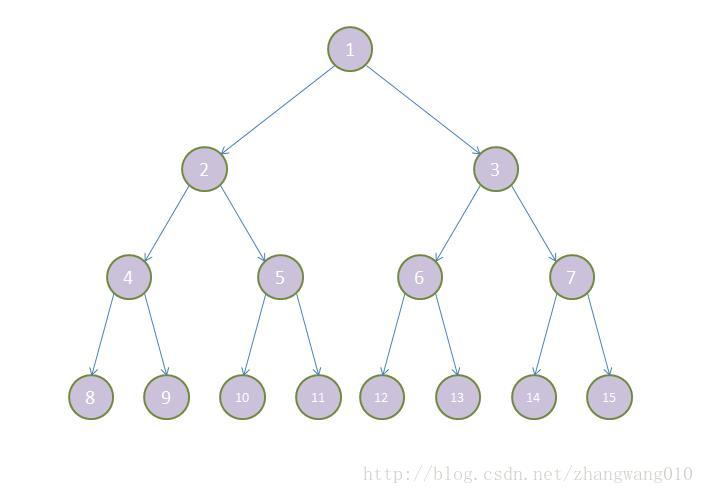
完全二叉树是指一颗二叉树必须能按层连续编号.如图就是完全二叉树,也是满二叉树:

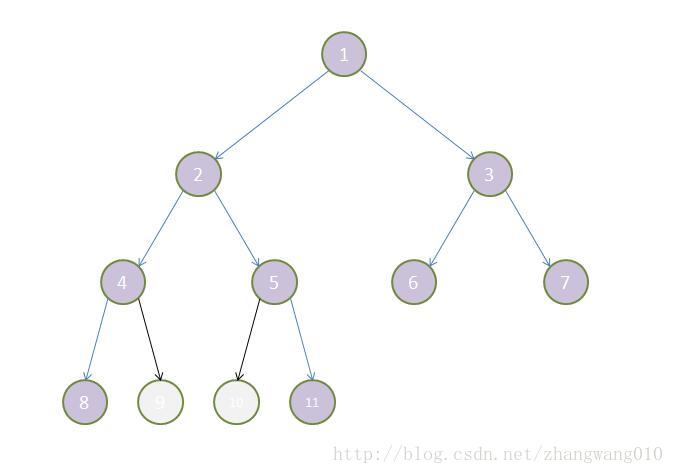
如下图也是完全二叉树,但不是是满二叉树:

如下图不是完全二叉树(9, 10 两个节点被剪掉)

完全二叉树的有趣的特性:

当用数组存储完全二叉树时可以用节点编号作为数组下标。这是有以下特性：

• 节点arr[i] 的右孩子等于arr[i*2]; 左孩子等于arr[i*2+1];
• 节点arr[i] 的父节点等于 arr[i/2] (当i/2= 0时,arr[i] 是根节点)
• 完全二叉树的深度/高度等于 : L = log2 (size+1) ; L向上取整
• 完全二叉树的最大节点数量s = (2^n)-1，n = 树的高度
• 应为二叉树的逐层增长规律与2的指数增长相似.所以这些特性都可以以此理解.