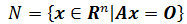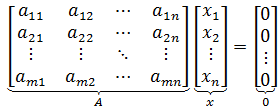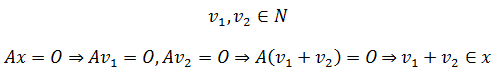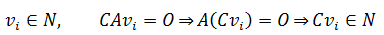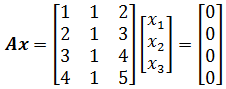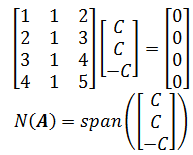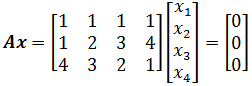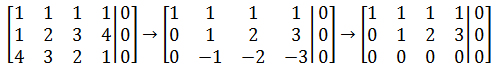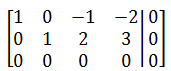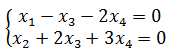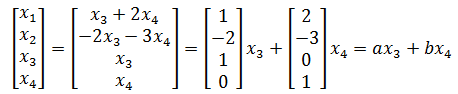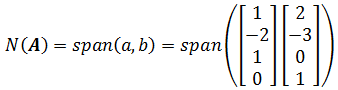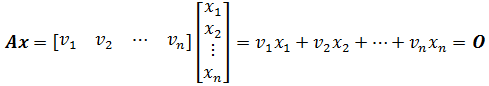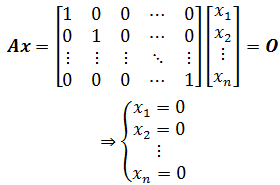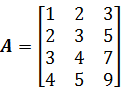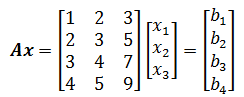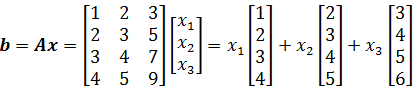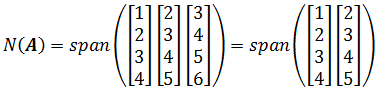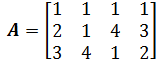零空间

　　先看定义。A是m×n矩阵，x是列向量，如果存在向量集合N，满足：

　　则称N是A的零空间。

零空间的意义

　　从定义看出，零空间是方程Ax = 0的所有解的集合：

　　A的零空间关心的是方程方程Ax = 0的解，准确地说是解所张成的空间，方程等于零向量也是零空间中“零”的含义。因为x∈Rⁿ，零空间关心的又是x的解，所以x张成的空间也在Rⁿ中，那么它是否是Rⁿ的子空间呢？

　　首先，0向量是方程的一组解。再假设v₁,v₂也都是方程的解，现在来看加法封闭性：

　　v₁,v₂满足加法封闭性。最后验证数乘封闭性，C是任意常数：

　　v也满足数乘封闭性，所以零空间也是Rⁿ的子空间。既然零空间是子空间，子空间又必须包括零向量，当Ax = b，b≠0时，由于没有全零解，A一定没有零空间。

找出零空间

　　我们已经知道了零空间的意义，如何找出零空间呢？

　　先看一个例子：

　　示例比较简单，除了全零解之外，方程组还有多组解，具体来说，如果C是任意常量，则：

　　在R³空间中，N(A)是过原点的直线。

　　再来个稍微复杂点的例子：

　　只需求解方程组就可以了，方法之一是将A化为行最简阶梯矩阵：

　　为了求解方便，我们的目标是让方程组的未知数尽量少，所以还可以进一步化简，让台角上方全为0：

　　将行最简阶梯矩阵转换为方程组：

　　两个方程，四个未知数，方程组有无数解，A的零空间是整个R⁴还是R⁴的其它子空间呢？回答这个问题前，还需要对方程组进一步转化：

　　x₃，x₄可以是任意实数，a，b是线性无关的，所以A的零空间就是a和b张成的空间：

　　具体来说，A的零空间是R⁴空间内过原点的一个平面，当然也是R⁴的子空间。

零空间与线性无关

　　再来关注一下Ax = 0中A的性质，A_m×n由n个列向量组成：

　　如果A是线性无关的，意味着方程组只有一个全零解，或者说，这个方程的解集是A的零空间，并且这个零空间只包含零向量。此时，A应当可以化简成单位矩阵：

　　结论是，当A是满秩方阵或列满秩的长方矩阵时，A的零空间只有零向量（仅仅是行满秩时就不一定了）。

列空间

　　如果A是m×n矩阵，那么A的列空间是A中所有列向量张成的空间。A的列空间用C(A)表示：

　　C(A)显然是R^m的子空间。

列空间的意义

　　先召唤一个矩阵：

　　三个向量不能构成整个R⁴空间，它只能构成R⁴的子空间。那么列空间的意义何在呢？ 还是要结合方程来看，零空间关心的是Ax = 0的解；列空间关心的是，在Ax = b中，什么样的b才能让方程有解。对于任意的b，方程并不总是有解，比如下面这个：

　　四个方程，三个未知数，方程组可能无解。从向量空间上看，三个向量无法充满整个四维空间，所以肯定有很多b不是这三个向量的线性组合。同时，这个方程组也可能是有解的，什么样的b才能使方程组有解呢？一个简单的办法是先写出x，然后根据b = Ax反推出b：

　　可以看到，b是A的线性组合，所以b一定在A的列空间内，此时Ax = b有解；反之，如果b不在A的列空间中，意味着Ax = b无解，这就是列空间意义了。

在上面例子中，A的第三个列向量可以由前两个的线性组合表示，因此A的列空间是R⁴的二维子空间：

列空间的基

　　我们已经理解了列空间，怎样计算列空间的基呢？先来看个例子：

　　A的列空间可以直接写成：

　　这样写似乎没错，但是A的四个列向量是否是线性组合呢？肯定不是，因为C(A)至多能张成R³空间，只需要三个向量就够了，所以A的四个向量中至少有一个是多余的，这就需要去掉多余的向量，求得列空间的基，这需要运用零空间的知识进行一些计算。首先将A转换为行最简阶梯矩阵，在此基础上让台角上方全为0：

　　A最终化简为行最简阶梯矩阵，阶梯的台角代表主元：

 　　这样看来主元的个数等于矩阵的秩。在R中，1、2两列是主元所在的列，它们是线性孤立的，其它列都可以用它们的线性组合表示，这也意味着1、2列的前身——A的1、2两列是线性孤立的。因此，只要确定了主元，就可以将列空间的基用主元所在的列数表示，本例中：

示例

示例1

　　看看哪些是R³的子空间？

　　首先回顾一下子空间，子空间包括零向量，子空间内所有向量的线性组合依然在子空间内。

　　1.这里描绘了向量分量间的关系是线性的，可以将其转换为方程：

　　<a₁,a₂,a₃>是<1,1,-1>的零空间，零空间是R³的子空间。

　　2.三个分量不是线性关系了，这意味着八成不是子空间，可以随意列举几个向量。当a₁ =1,a₂ =1时，a₃ = a₁ a₂ = 1，<a₁,a₂,a₃> = <1, 1, 1>，由于子空间对数乘封闭，所以<2, 2, 2>也应该在子空间内，但此时 a₃ ≠ a₁a₂，所以问题2的条件不能构成子空间。

　　3.先将表达式化简：

　　<a₁,a₂,a₃>是<1, 0, -1>和<1, 0, 1>的线性组合，是子空间。

　　4. 还是先将表达式化简：

　　注意到第二个分量是1，是定值，无法构成零向量，问题4的条件不能构成子空间。

 示例2

　　找出Ax=b的列空间。

　　首先化简为最简行阶梯矩阵：

　　主元是1、2、4列，列空间是主元所在的列：

　　作者：我是8位的