信号采集频率_频率采样「建议收藏」

参考：
采样率与频率之间的关系_TaoTaoFu的博客-CSDN博客_采样频率和信号频率之间的关系”>

<2>信号频率、采样频率、采样点数 – 简书

<3>2.3 信号采样与采样定理 – 物联网前沿实践

<4>语音信号处理——常识与基本概念 – 凌逆战 – 博客园

<5>信号的时间域分辨率和频率域分辨率 – 知乎

<6>基础知识：采样频率和频率分辨率-面包板社区

0.基础概念：

0.1 信号频率（f）

        连续时间信号频率就是信号的频率，影响的是信号的发生函数。

        以声波信号为例，声波每秒钟振动的周期数称为声波的频率，单位是赫兹 (Hz)。

        一般来说，人耳可以听到的声波频率大概在20 Hz​到20 kHz之间，频率超过20 kHz​的声波我们称为超声波，低于20 Hz​的声波称为次声波。

0.2 信号周期 (T)

0.3 采样率， 采样频率，采样速度（fs）

        每秒从连续信号中提取 并 组成离散信号的采样个数，它用赫兹（Hz）来表示。

        以语音为例，通俗的讲采样频率是指计算机每秒钟采集多少个声音样本。

        意义：采样率决定了采样的精度。采样频率越高，即采样的间隔时间越短，则在单位时间内计算机得到的声音样本数据就越多，对声音波形的表示也越精确。

        注意：采样频率必须大于信号的频率（不失真），fs/N（频率分辨率）越小，精度越高，通过补0增加的FFT点数无法提高FFT精度。

0.4 采样周期，采样时间（Ts, dt）

        波形中相邻两点间隔的时间就是采样频率（fs）的倒数，它是采样之间的时间间隔。

0.5 采样点数（N）

        采样点数是一次向PC端发送的数据量包含的点数，采样点数决定了每次传到PC内的数据量。
就是每个周期采了几个点。

N =T/Ts         Ts=dt = 1/fs

       FFT、IFFT的采样点数必须是2的指数，在频域一个频点对应时域的一次采样，所以FFT的点数自然就是2048、1024、512、256、128.

0.6 阵列信号快拍数（snaps）

        快拍数一般是指 时域上的采样点数，也就是snaps

        全部阵元在时域的一次采样.如果阵元数为M，那么通常用 X(t) 来表示一次采样，维数为 M*1 

0.7 频率分辨率(f0):

详细看：基础知识：采样频率和频率分辨率-面包板社区

        频率分辨率可以理解为在使用DFT时，在频率轴上的所能得到的最小频率间隔。实际是作FFT时谱图中的两条相邻谱线之间的频率间隔，也有称作步长。

        N为采样点数，fs为采样频率，Ts为采样间隔。所以 N*Ts 就是采样前模拟信号的时间长度T，信号长度越长，频率分辨率越好。

        注意：只有增加点数的同时导致增加了数据长度T才能使分辨率越好。

0.8 补零：

        在做DFT时，常常在有效数据后面补零达到对频谱做某种改善的目的

        补零并没有增加有效数据的长度，仍然为T。

补零的好处：

1. 使数据N为2的整次幂，便于使用FFT。
2. 补零后，其实是对DFT结果做了插值，克服“栅栏”效应，使谱外观平滑化。我把“栅栏”效应形象理解为，就像站在栅栏旁边透过栅栏看外面风景，肯定有被栅栏挡住比较多风景，此时就可能漏掉较大频域分量，但是补零以后，相当于你站远了，改变了栅栏密度，风景就看的越来越清楚了。
3. 由于对时域数据的截短必然造成频谱泄露，因此在频谱中可能出现难以辨认的谱峰，补零在一定程度上能消除这种现象。

关系：

        产生信号的总时间长度 t  = Ts * 采样数N = 采样数N / fs

        产生信号的周期数 = 总时间长度/T = 总时间长/信号频率 

1.举例：

1.0 采样频率

        常见到的音频文件采样率多为44.1KHz。

        假设我们有2段正弦波信号，分别为20Hz和20KHz，长度均为一秒钟，以对应我们能听到的最低频和最高频，分别对这两段信号进行40KHz的采样。

结果：

        20Hz语音每次振动被采样了

        20KHz语音每次振动被采样了

 所以在相同的采样率下，记录低频的信息远远比高频的详细。

1.1 奈奎斯特采样定律

奈奎斯特采样定律：

        采样周期要小于整数周期的1/2，即采样频率应该大于原始频率的2倍。否则将发生混叠（相位/频率模糊）。

        实际例子：你产生车轮倒转的错觉的时候，说明你眼睛的采样频率过低从而得出了错误结论

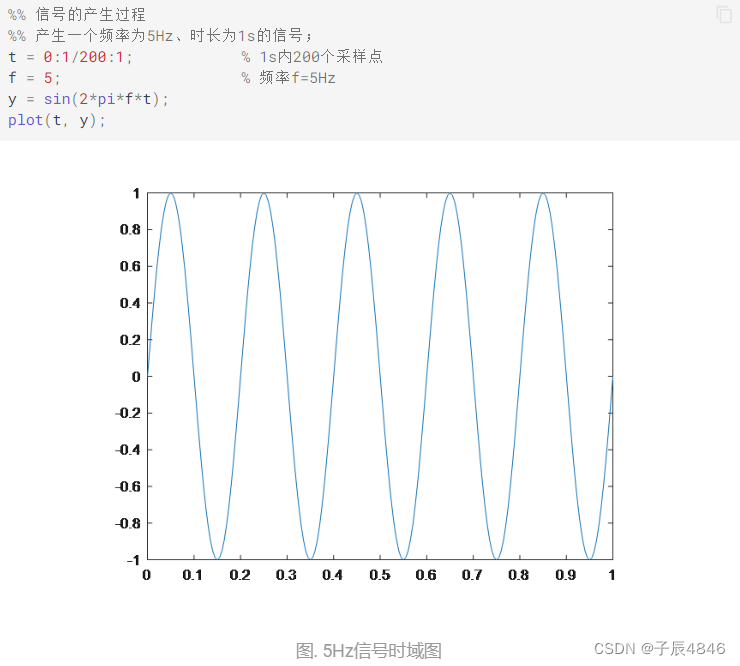
         一般的信号频率为5Hz，采样频率 为200Hz

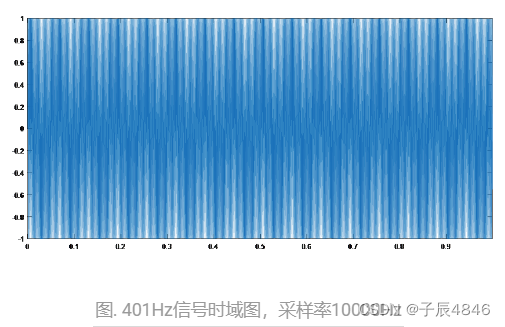
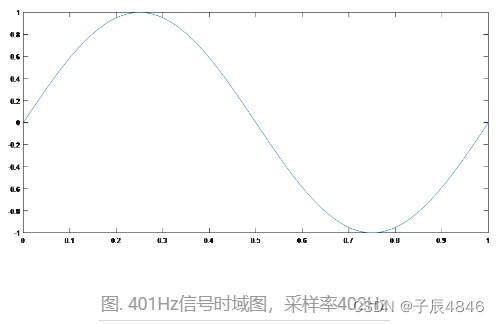
信号是401Hz的，采用远大于401Hz两倍的采样率10KHz来采样。

2.关于频率分辨率的2种解释

详细看：基础知识：采样频率和频率分辨率-面包板社区

• 关于频率分辨率的2种解释

• 补零

• DFT考虑窗函数的注意点，各种窗函数的优缺点

• 时域、频域采样定理

• 分析频率、采样点数、谱线数的设置要点

3.语音相关：

详细看：语音信号处理——常识与基本概念 – 凌逆战 – 博客园

今天的文章信号采集频率_频率采样「建议收藏」分享到此就结束了，感谢您的阅读。