Plackett-Luce模型算法介绍

1 简介

　　最近学习了一下机器学习上经典的排序融合算法(Rank Aggregation)——Plackett-Luce模型，它的核心思想已经深深融入到我们生活的每个角落，大到总统选举，小到生活上小抉择。虽然目前来看，P-L算法算是最简单的一种排序融合(Rank Aggregation)方式之一，但是我认为还有很多值得借鉴的地方，尤其在机器学习、计算机视觉方向上，经典的东西永远是值得学习和回味的。
　　Plackett-Luce模型最早是Luce(1959年)和Plackett(1975年)分别提出和完善的算法，它是一种多项逻辑回归的自然概括模型。随后又被很多研究者一步步改进，其中解决参数估计的最主要方式有两种，一种是2004年Hunter提出的基于MM(Minorization-Maximization)算法的MLE最大似然估计方法，另一种是2009年Guiver和Snelson提出的使用信息传递方式的贝叶斯方法(论文在后面会贴出)。

2 模型思想

2.1 简单举例

　　我们首先通过一个班干选举的例子来看看PL模型所要解决的问题。假如现在班级有五个同学O1、O2、O3、O4、O5参加班干选举，老师本来想自己做权责，由于五位同学在学习成绩，体育劳动等等表现方面都各有优势，所以其中任何一名参选者做为班长的概率，也就是数学上权重并不明朗。老师决定做一次班级选举，选举规则就是班上其他同学互不议论的情况下进行不记名投票，每位投票者写下自己认为合理的排序(Rank)，然后老师统计结果(Aggregation)。这样，四名同学中得票最高的担任班长，次之的担任副班长，再次之的分别担任学习委员、劳动委员，得票最少的则落选。
　　我们先来看，假设老师有个很好的平时表现衡量标准，也就是老师客观计算出来了这五位同学平时表现综合分数，然后标准化为权重依次为[w1,w2,w3,w4,w5]（权重的总和为1）。最后就可以根据这个权重大小依次委派他们班干职务。模型如下：　　
1. 五名同学参选，对应客观衡量标准的权重

2. 先依次计算每个同学被选上班长的概率

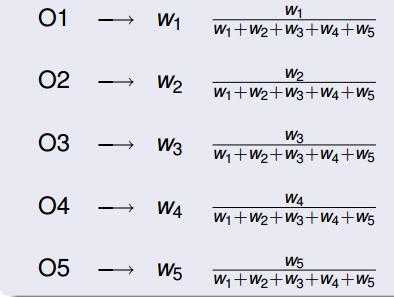
3. 假设O4同学计算后概率最大，所以理应O4同学担任班长

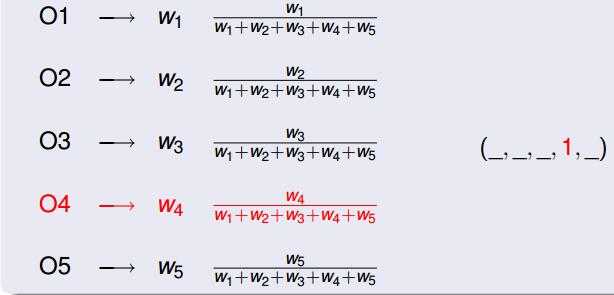
4. 然后在剩下同学中计算得到O5同学概率最大，O5担任副班长

5. 依次这样计算下去，排得顺序为：O4>O5>O2>O1>O3.

6. 这样，我们就可以计算出按这个顺序排列的总概率为5次步骤计算概率的乘积，如上图所示。按分数评判规则来说，这个O4>O5>O2>O1>O3排序概率结果，也会比其他任何排序概率结果高。所以排序结果相对很客观。
　　以上过程可以总结为以下这个数学模型：
　　
　　但是由于老师并不能很好的从他们五位平时表现定出一个衡量标准，所以希望通过投票的方式来解决问题。每个同学都有一个主观上Rank排序，数学上称为存在一定噪声或误差的结果，老师希望从所有同学主观的排序结果上，Aggregation融合出一个最理想的排序方案。
　　好了，现在问题就明朗了，原来投票的最终目的是，从一堆主观上的同学选举排序结果上来融合统计出一个最为客观的最终排序结果，即学习出一个衡量标准，计算出每位候选者最客观的能力值。

2.2 Plackett-Luce模型

　　从2.1举例上，我们可以总结出Plackett-Luce模型的目的：
　　
　　模型定义：
　　
　　
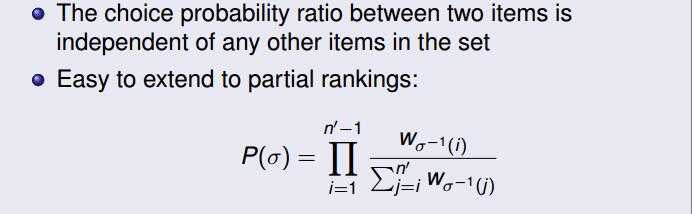
　　模型参数：W={
Wi |　 i = 1, 2,… ,m ,　Wi ∈[0,1], 　∑Wi=1 }。
　　每个参数对应的即相应的alternative(待排序数据元素)排在第一位的概率。
　　我们希望通过各种方法最快最准确的学习出上面的参数，从而利用Plackett-Luce模型能很好的应用在数据排序上，评判排序结果。至于具体学习得到PL模型参数的方法，这里不再详细介绍，前面已提到目前最主流的两种方式，博文最后有提出文章题目，感兴趣的读者可以自行阅读论文。
　　Plackett-Luce模型思想很简单，但是真的很经典，现在广泛的应用在我们生活当中。当然，还有许多更深入的再研究，例如k-PL模型，即k个PL模型混合学习，详细内容也请各位自行阅读相关论文，下面有贴出论文题目。
　　
相关论文：
John Guiver, Edward Snelson(2009). Bayesian inference for Plackett-Luce ranking models.
Hunter, D. R. (2004). MM algorithms for generalized Bradley-Terry models.
Zhibing Zhao, Peter Piech , Lirong Xia. Learning Mixtures of Plackett-Luce Models