matlab中两点的距离_matlab星下点轨迹绘制

背景：两个天线分别坐落在两个山头上（或者其他什么地方均可，中间要保证无阻碍物），它们的波束角度都很小，大概为一度，且相距很远（几十公里），无法直接用望远镜观察位置来手动调整，因此需要通过计算调整各自的方位和仰角。两个点的经纬度和海拔均为已知条件。

首先，地球并不是完美的球体，它更接近一个两极比赤道更扁的椭球。查阅资料可得，赤道半径约为6378137米，而极半径约为6356752米，中间大概相差了22000米，因此其造成的误差已经无法忽略。对于这种情况，即使两个点的海拔一样高，在实际空间上也会有一定的高度差，会需要仰角的小幅度偏移。

我的思路：

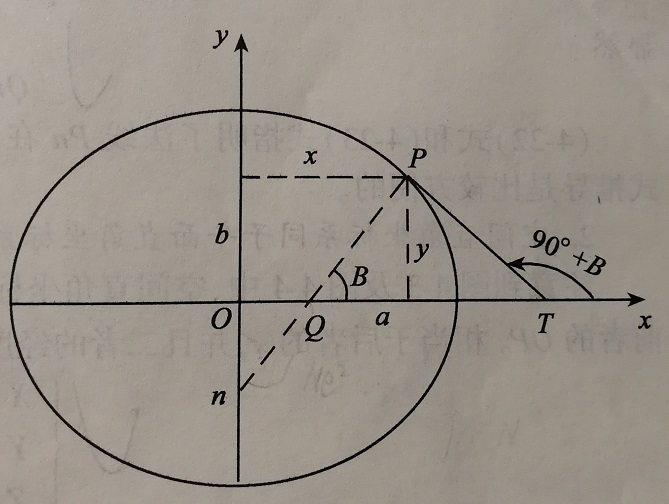
第一步，将经纬度和海拔转化成常用的笛卡尔坐标（xyz），这样计算起来比较熟悉和方便。通过对椭球中任意一个子午面的分析可得出换算公式：

图中的y对应笛卡尔坐标系内P点的z轴，x是坐标系内P点投影向量在（x，y）与原点之间连接的线段。原理类似于球体极坐标转换成直角坐标系，根据勾股定理等可推出：

P(x) = ( N + 海拔 ) .* cos( 纬度) .* cos( 经度)
P(y) = ( N + 海拔 ) .* cos( 纬度) .* sin( 经度 )
P(z)= ( ( 1.0 – e2)

今天的文章matlab中两点的距离_matlab星下点轨迹绘制分享到此就结束了，感谢您的阅读。