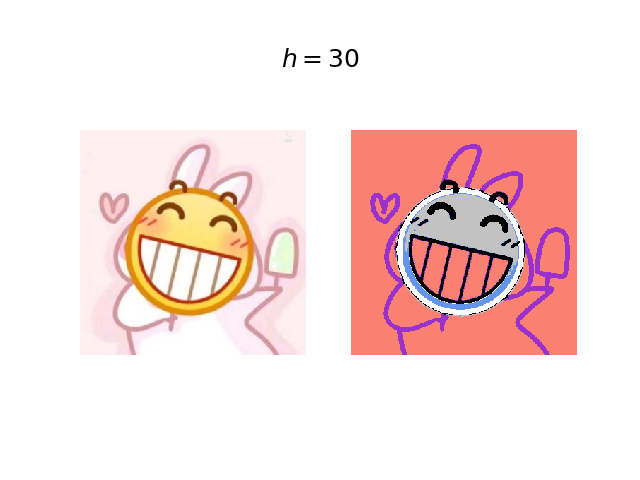大黄脸头像_图像分类算法

前言

  前面几篇博客已经介绍过了基于距离的聚类算法$($K-Means、K-Means++和MeanShift$)$和基于密度的聚类算法$($DBSCAN$)$，当然，除此之外还有像层次聚类、谱聚类等这些聚类算法还没有学习到，以后若涉及到再做记录。本篇博客就主要借助机器学习中常用的一个库——scikit-learn来实现图像分割，没错，就是我的头像ｂ（￣▽￣）ｄ

  这张图片$(320\ast 320)$是三通道的，相当于数据的维度为3，由此就根据像素值$($颜色$)$来实现聚类，即分割图像。

1. K-Means分割图像

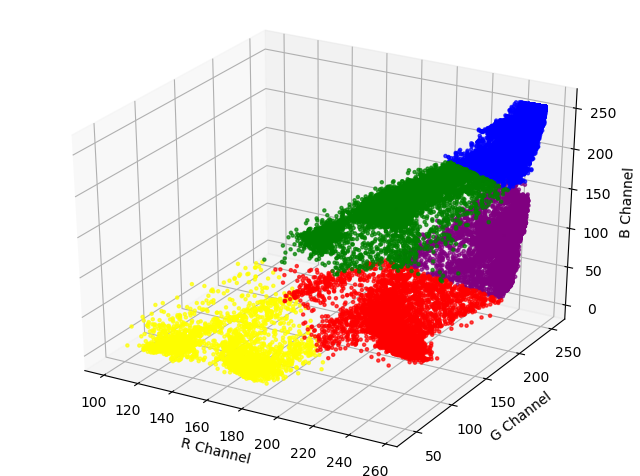
  为了与前面几篇博客保持一致，先在坐标轴上简单看一下聚类的结果，只不过是将前面的二维坐标变成了三维坐标$(R,G,B)$，代码如下：

import numpy as np
from sklearn.cluster import KMeans
import imageio
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


def draw_picture(data_arr, cluster_centers, labels):
    dots1 = data_arr[labels == 0]
    dots2 = data_arr[labels == 1]
    dots3 = data_arr[labels == 2]
    dots4 = data_arr[labels == 3]
    dots5 = data_arr[labels == 4]

    fig = plt.figure()
    ax = Axes3D(fig)

    ax.scatter(dots1[:, 0], dots1[:, 1], dots1[:, 2], marker='o',
               color='blue', alpha=0.7, label='dots1 samples', s=5)
    ax.scatter(dots2[:, 0], dots2[:, 1], dots2[:, 2], marker='o',
               color='green', alpha=0.7, label='dots2 samples', s=5)
    ax.scatter(dots3[:, 0], dots3[:, 1], dots3[:, 2], marker='o',
               color='red', alpha=0.7, label='dots3 samples', s=5)
    ax.scatter(dots4[:, 0], dots4[:, 1], dots4[:, 2], marker='o',
               color='purple', alpha=0.7, label='dots4 samples', s=5)
    ax.scatter(dots5[:, 0], dots5[:, 1], dots5[:, 2], marker='o',
               color='yellow', alpha=0.7, label='dots5 samples', s=5)
    ax.scatter(cluster_centers[:, 0], cluster_centers[:, 1], cluster_centers[:, 2], marker='x',
               color='black', alpha=0.7, label='centroids', s=5)

    ax.set_xlabel('R Channel')
    ax.set_ylabel('G Channel')
    ax.set_zlabel('B Channel')

    plt.savefig('./result_3d_s.png')
    plt.show()


if __name__ == '__main__':
    img = imageio.imread('./touxiang.png')
    img_flatten = img.reshape(-1, 3)

    kmeans = KMeans(n_clusters=5, init='k-means++', n_init=10, max_iter=300,
                    tol=1e4, verbose=0, random_state=1024, n_jobs=1)
    kmeans.fit(X=img_flatten)

    cluster_centers = kmeans.cluster_centers_
    labels = kmeans.labels_

    draw_picture(img_flatten, cluster_centers, labels)
    

  上面的参数在这篇博客中有介绍，在这里就不过多解释了，结果如下：

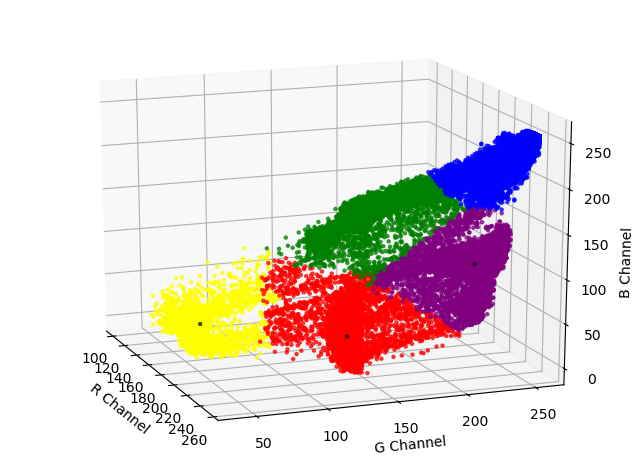
  在Pycharm中默认显示的3D图像是不可以旋转的，可以通过如下设置：File$-->$Settings$-->$Tools$-->$Python Scientific$-->$Show plots in tool window$($前面的√去掉$)$$-->$Apply$-->$OK，然后通过旋转就可以看到聚类中心了$($即图中黑色圆点$)$。

  OK，fine，其实图像的结果也和上面一样了，只不过不把它放到坐标轴上，而是以数组的形式存起来，将下面的seg_img函数替换掉上面的draw_picture即可，代码如下：

def seg_img(img, labels):
    labels = labels.reshape(320, 320)
    img_seg = np.array(np.zeros(shape=(320, 320, 3), dtype=np.uint8))
    img_seg[labels == 0] = [250, 128, 114]
    img_seg[labels == 1] = [194, 194, 194]
    img_seg[labels == 2] = [153, 50, 204]
    img_seg[labels == 3] = [255, 255, 255]
    img_seg[labels == 4] = [100, 149, 237]

    plt.subplot(121)
    plt.axis('off')
    plt.imshow(img)

    plt.subplot(122)
    plt.axis('off')
    plt.imshow(img_seg)

    plt.savefig('./result_5k.png')
    plt.show()
    

  如果划分为四个类别，就是这样子的：
  如果划分为五个类别，就是这样子的：

  注：上面的颜色会随机分给各个类别。

2. Mean Shift分割图像

  实现流程和上述一样，只不过函数变成了MeanShift，这里只贴出改动的部分，代码如下：

  MeanShift函数的部分参数已注释，更详细的说明，请参考官方文档。

from sklearn.cluster import MeanShift


if __name__ == '__main__':
    img = imageio.imread('./touxiang.png')
    img_flatten = img.reshape(-1, 3)

	# bandwidth: 半径(或带宽), float型, 默认None
    # 如果没有给出, 则使用sklearn.cluster.estimate_bandwidth计算出半径(带宽)(可选)
    # seeds: 圆心(或种子), 数组类型, 即初始化的圆心, 默认None(可选)
    # 如果未设置, 则通过clustering.get_bin_seeds计算种子, 并使用带宽作为网格大小以及其他参数的默认值
    # bin_seeding: 布尔值. 如果为真, 初始内核位置不是所有点的位置, 而是点的离散版本的位置, 其中点被分类到其粗糙度对应于带宽的网格上
    # 将此选项设置为True将加速算法, 因为较少的种子将被初始化. 默认值: False, 如果种子参数(seeds)不为None则忽略
    # n_jobs: 任务使用的CPU数量
    # 如果bandwidth不设置, 代码运行会消耗较多时间
    meanshift = MeanShift(bandwidth=20, seeds=None, bin_seeding=True,
                          min_bin_freq=10, cluster_all=True, n_jobs=1)
    meanshift.fit(X=img_flatten)

    cluster_centers = meanshift.cluster_centers_
    labels = meanshift.labels_

    seg_img(img, labels)
    

  不同的半径会有不同的结果，可以去尝试不同的设置，部分结果如下：

  搞错了，再来(づ｡◕ᴗᴗ◕｡)づ（感觉还是蛮像的！哈哈哈哈哈哈哈哈哈）

3. DBSCAN分割图像

  实现流程和上述一样，只不过函数变成了DBSCAN，这里只贴出改动的部分，代码如下：

  DBSCAN函数的部分参数已注释，更详细的说明，请参考官方文档。

from sklearn.cluster import DBSCAN


if __name__ == '__main__':
    img = imageio.imread('./touxiang.png')
    img_flatten = img.reshape(-1, 3)

    # eps: 两个样本之间的最大距离, 即半径, 默认为0.5
    # min_samples: 作为核心点的邻域(即以其为圆心, eps为半径的圆, 含圆上的点)中的最小样本数(包括点本身)
    # 即MinPts, 默认为5
    # 其他参数可参考官方文档
    dbscan = DBSCAN(eps=0.5, min_samples=5)
    dbscan.fit(X=img_flatten)

    labels = dbscan.labels_

    seg_img(img, labels)
    

  运行结果如下：

  对于图片来说，运行较占内存，可能上面的参数还要再配置一下。然后我又多尝试了几次，结果MemoryError了∑(っ°Д°;)っ卧槽，无情。官方是这样说的：
  大样本量的内存消耗
  默认情况下，此实现的内存效率不高，因为它在无法使用kd树或球树的情况下$($例如，稀疏矩阵$)$构造了完整的成对相似度矩阵。该矩阵将消耗$n^2$个浮点数。解决此问题的几种机制是：

• 将OPTICS聚类与该extract_dbscan方法结合使用 。OPTICS集群还可以计算完整的成对矩阵，但是一次只能在内存中保留一行$($内存复杂度$n)$。
• 可以用内存有效的方式预先计算稀疏半径邻域图$($假定缺少的条目不在eps之内$)$，而dbscan可以使用metric =’precomputed’在其上运行。
• 可以压缩数据集，方法是删除精确重复项$($如果数据中出现重复项$)$，或者使用BIRCH。这样，对于大量的点，就只有相对较少的代表。然后，可以在拟合DBSCAN时提供一个sample_weight。

  我尝试用官方的方法去设置，然而并没有有效解决，然后受到上面第三条的启发，我就把图像缩放到了$128\ast 128$，问题得以解决。
  为了方便调参，将数据进行了归一化处理，修正代码如下：

	img_flatten = img.reshape(-1, 3) / 255.0

  调整后的运行结果如下：

  eps越大，聚类的类别就越少；MinPts越大，聚类的类别也越少。根据经验，最好将MinPts设置为数据中特征的数量，eps使用小值通常是首选。

结束语

  本篇博客在使用DBSCAN时出了一些问题，图像的尺寸有些大，处理不了，然后就将图像进行放缩了。另外，由此也可以看出DBSCAN算法的弊端，就是参数需要不断去调整，相对来说还是较麻烦的，不过我看网上有说可以借助k-distance图来找最佳的eps，当然了官方也说有优化的方法，这些还有待探索。继续加油ヾ(◍°∇°◍)ﾉﾞ

今天的文章大黄脸头像_图像分类算法分享到此就结束了，感谢您的阅读。