任意点 曲线距离_圆锥曲线光学性质的直观证明

问

怎么证明圆锥曲线的光学特性，最好有不用到求导的方法？

答

• 椭圆

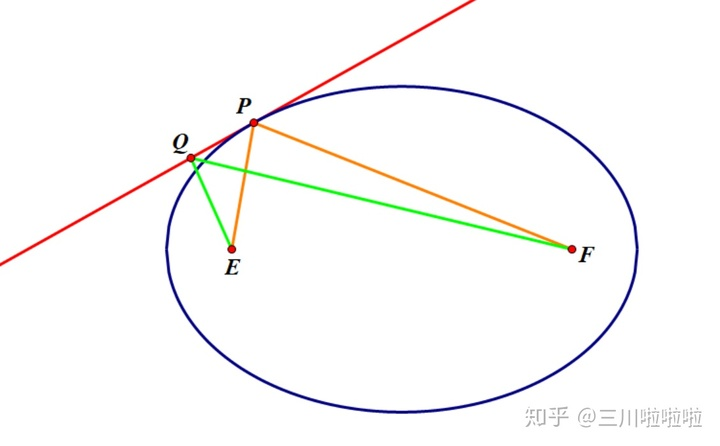
由椭圆的定义——平面上，到定点

与

距离之和为定值

的点的轨迹，这个定义蕴含着一个很显然的事实：

• 当
  在椭圆外时，有
  ；
• 当
  在椭圆上时，有
  ；
• 当
  在椭圆内时，有
  .

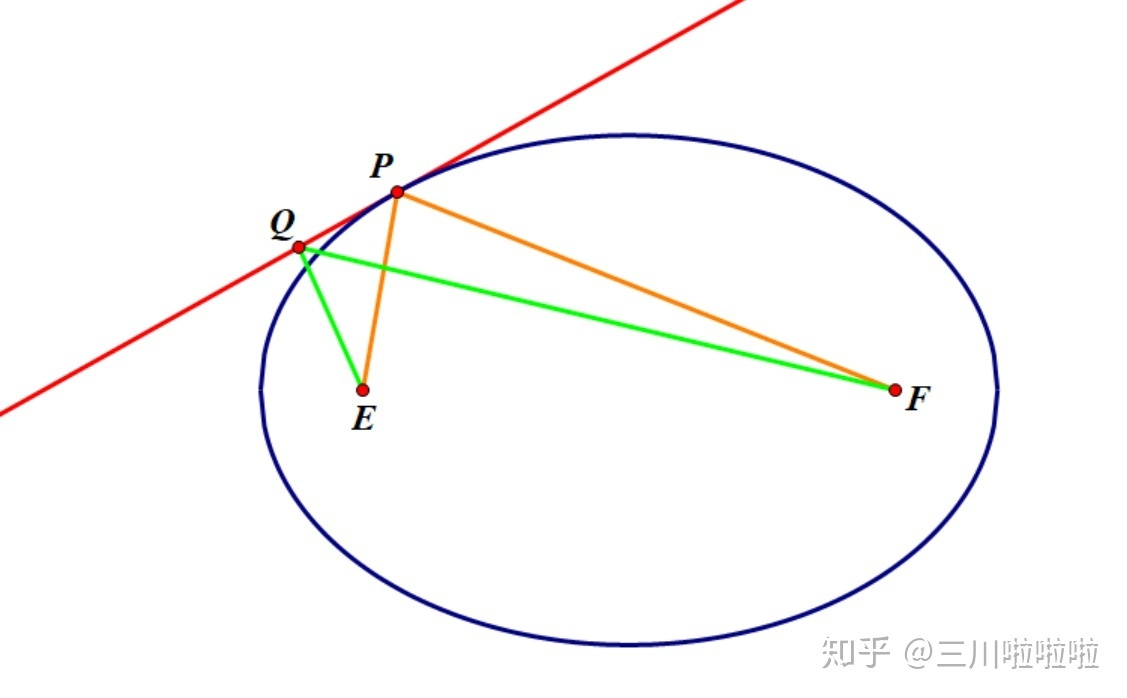
见上图，过椭圆上一点

的切线，除

点外切线上任意一点

都在椭圆外（凸性），于是由上面的观察得到：

所以

点是切线上到定点

与

距离之和最小点，故

点是反射点。

• 抛物线

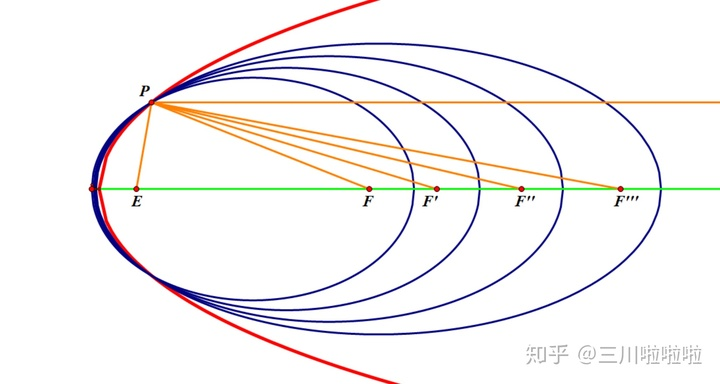
在理解椭圆光学性质的基础上，我们先固定一个焦点

，然后将另一个焦点

牵引到无穷远处，离心率

即椭圆最终变为抛物线，而此时反射光

的极限位置平行于椭圆长轴。

^[1]

• 双曲线

类似于椭圆的分析，不过我们要熟悉一个结论：

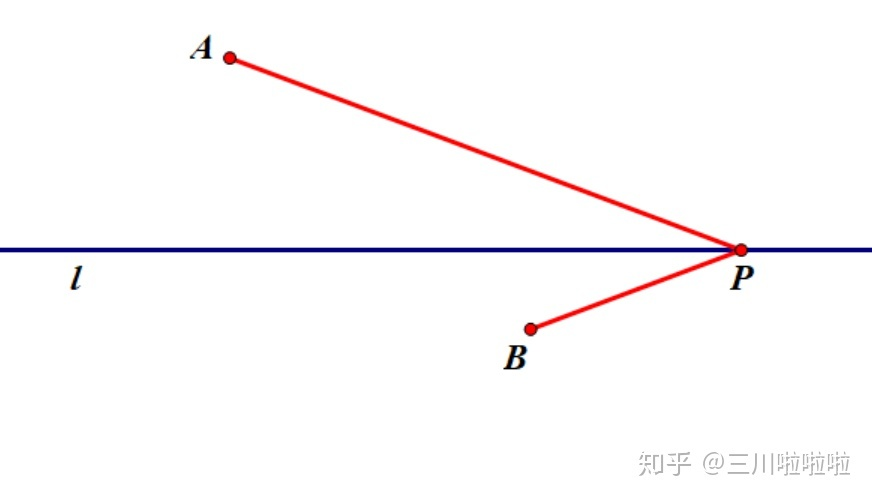
引理

如上图

，选取直线

上的动点

，使得

最大，当且仅当

平分

.

证

在

上取

点关于直线

的对称点

，于是

只需证明当取直线上其他点

时，总有

即可完成证明

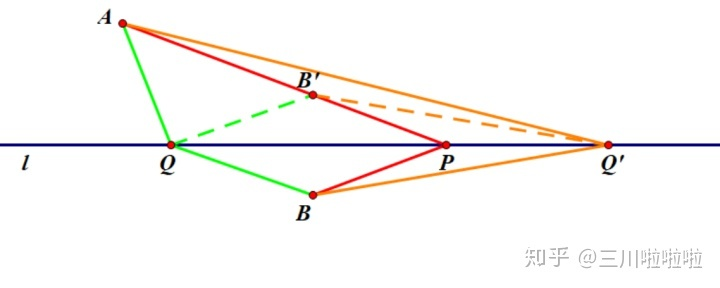
连接

，由

得

而在

中，由两边只差小于第三边立即可得

有了这个引理，那么接下来的分析顺理成章

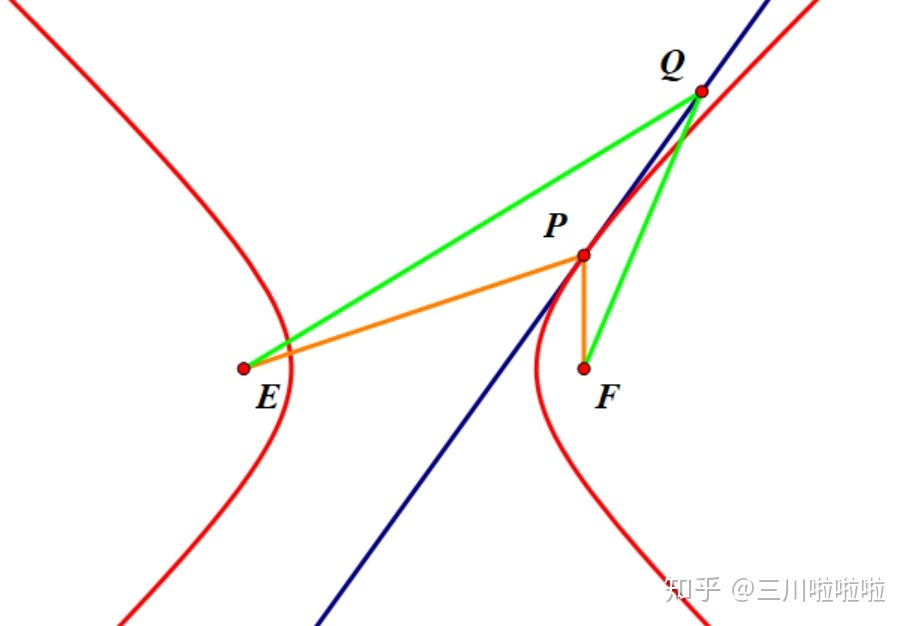
见上图，

是双曲线过

点的切线. 我们定义函数

，双曲线将平面分割为三个部分，我们命名焦点一侧的区域为“双曲线内部”，另一个连通区域为“外部”. 由双曲线定义蕴含以下事实：

• 当
  点位于双曲线内部时，
  ；
• 当
  点位于双曲线上面时，
  ；
• 当
  点位于双曲线外部时，
  ；

而切线

上仅有一点

满足

，其余各点

皆有

，所以

是切线

上的最大值点，也就是使得

由上引理，必有

平分

.

参考

1. ^希尔伯特《直观几何》