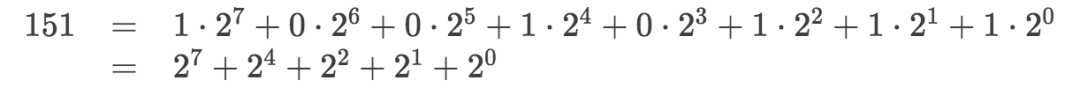椭圆曲线密码算法_椭圆曲线密码学导论pdf

密码学 – 椭圆曲线 ECC ED25519

椭圆曲线是一系列满足如下方程的点:
y^2 = x^3 + ax + b
并且
4a^3 + 27b^2 != 0

特性

1. 封闭性：因为椭圆曲线上的点相加，还是椭圆曲线上的点。
2. 结合律：P+(Q+R) = (P+Q)+R = 0
3. 单位元: 单位元是0, 即 P+0 = P
4. 逆元: 一个椭圆曲线上的点P的逆元，是相对x坐标的对称点
5. 交换律：P+Q = Q+P

标量乘法

nP = P + P + P + ... +P

• 计算标量乘法，最简单的方法是一个个P点相加
• 有个快速的计算方法：double后相加. “Double”主要是依次获得某个位对应的变量的结果。如果该位是1，就加到最后的结果中:
  

生成一个公钥

通常使用椭圆曲线算法，先选择曲线，计算椭圆曲线的阶，然后在这条曲线上找到最大的子群。找子群，就是寻找子群对应的生成元(G)。

从一个密钥（形式上是一个随机生成的数字k）开始，我们将它与曲线上预定义的点相乘，可以得到曲线上的另一个点，这就是相应的公钥K，而这个预定义的点叫作生成点G。生成点是作为secp256k1标准的一部分定义的，对于比特币而言，其所有密钥均使用相同G点。

K=kG

k是密钥，G是生成点，K是生成的公钥，也是椭圆曲线上的一个点

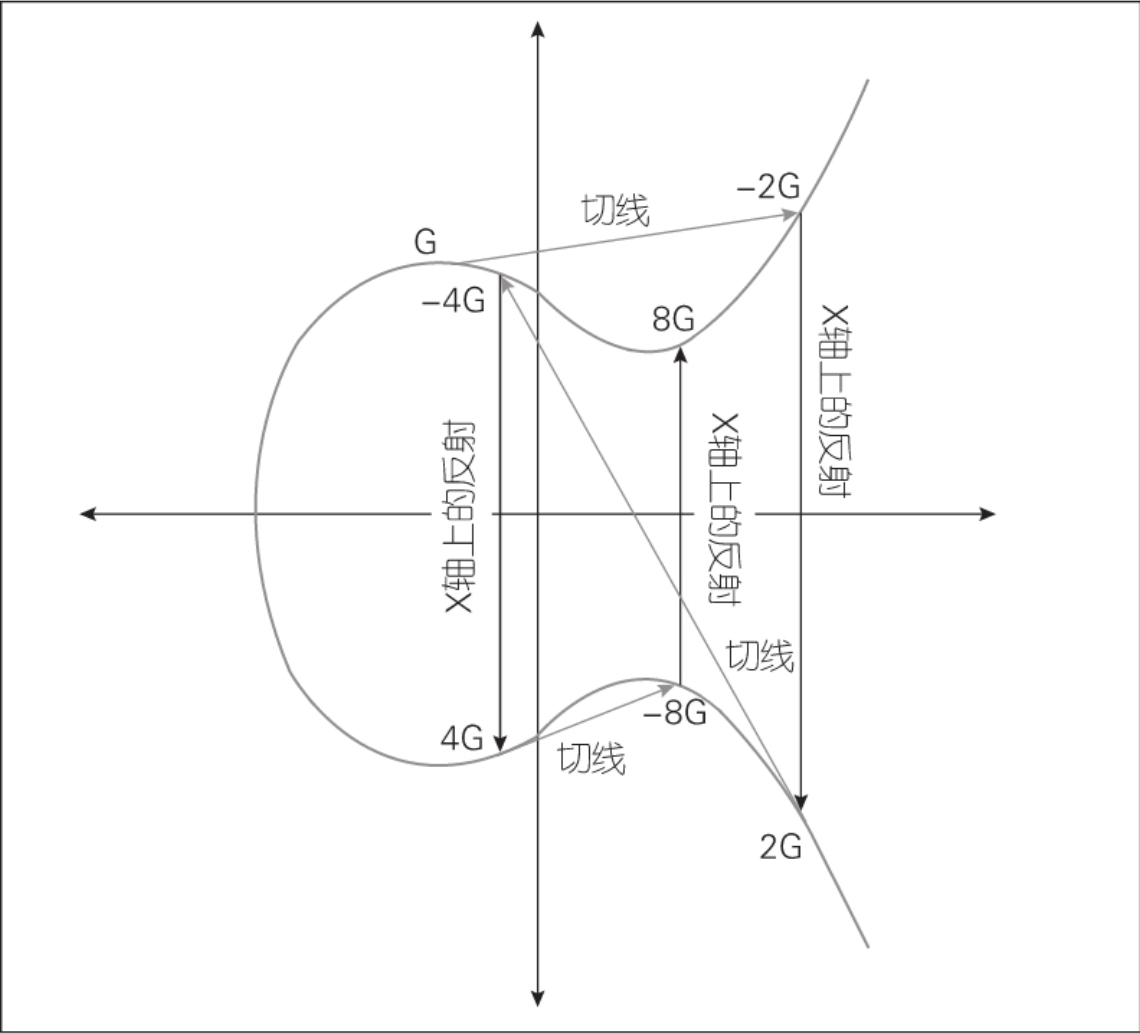
找到生成点G的倍数kG。也就是G相加k次

在椭圆曲线中，一个点与其自身相加等同于在这个点上画一条切线，找到切斜与曲线相交的点，相交点相对x轴对称的点就是我们要找的点

演示G在椭圆曲线上被整数k相乘

两大系列

• NIST系列曲线
  • 美国国家标准与技术研究院（National Institute of Standards and Technology, NIST）
  • 目前广泛使用
  • 代表: secp256k1
• 25519系列曲线
  • 著名密码学家Daniel J. Bernstein在2006年独立设计的椭圆曲线加密/签名/密钥交换算法
  • 目前最快
  • 代表: ed25519

ED25519曲线

Curve25519/Ed25519/X25519 是著名密码学家Daniel J. Bernstein在2006年独立设计的椭圆曲线加密/签名/密钥交换算法，与现有的任何椭圆曲线算法完全独立，其中Ed25519用于签名。

25519系列曲线自2006年发表以来，除了学术界无人问津，2013年爱德华·斯诺登曝光棱镜计划后，该算法突然大火，OpenSSH迅速增加了对25519系列的支持，RFC增加了SSL/TLS对X25519密钥交换协议的支持。

Curve25519的椭圆曲线方程如下:
y^2=x^3+486662*x^2+x, modulop=2^255-19

ed25519的椭圆曲线方程如下:
-x^2+y^2=1-(121665/121666)*x^2*y^2, modulop=2^255-19

25519算法的特点如下

• 完全开放设计。算法各参数非常明确，没有任何可疑之处，而目前广泛使用的椭圆曲线是NIST，系数有来历不明的随机种子, 如: secp256k1
• 安全性高。 实践上最安全的加密算法
  
• 速度快。25519系列曲线是目前最快的椭圆曲线加密算法，性能远远超过NIST系列。

参考:
https://mp.weixin.qq.com/s/-Pws7J_9DOvwxXJ-Ma9mig
http://mathworld.wolfram.com/EllipticCurve.html

往期精彩回顾:

区块链知识系列

密码学系列

共识系列

公链调研系列

以太坊系列

EOS系列

智能合约系列

Token系列

今天的文章椭圆曲线密码算法_椭圆曲线密码学导论pdf分享到此就结束了，感谢您的阅读。